Advanced High School Statistics: First Edition

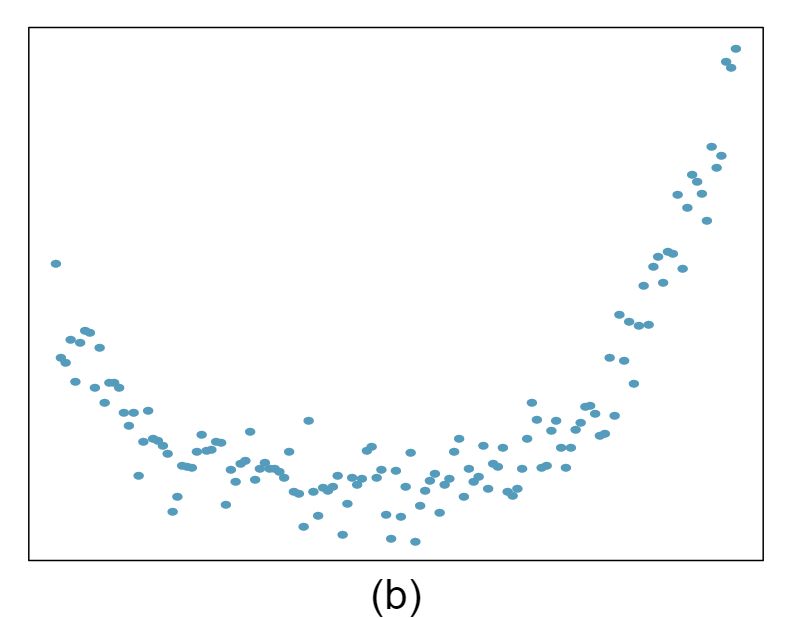
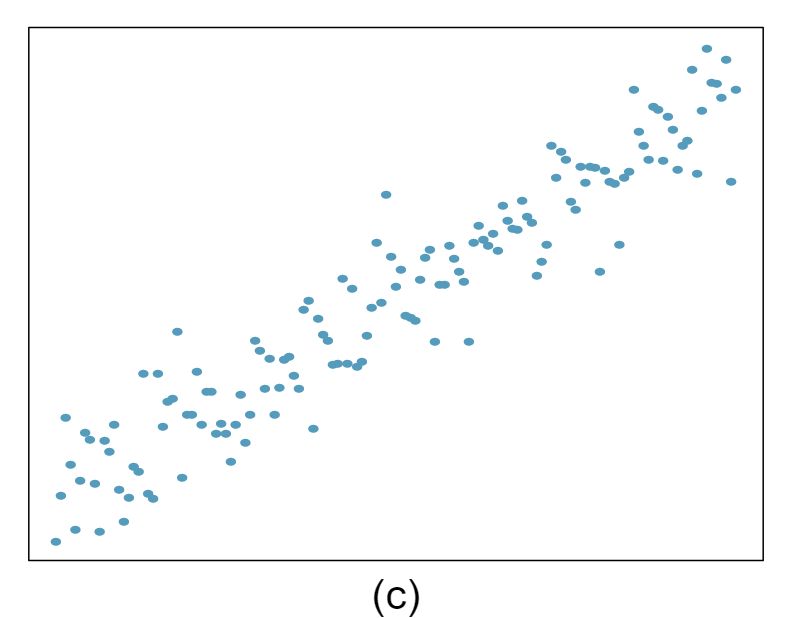
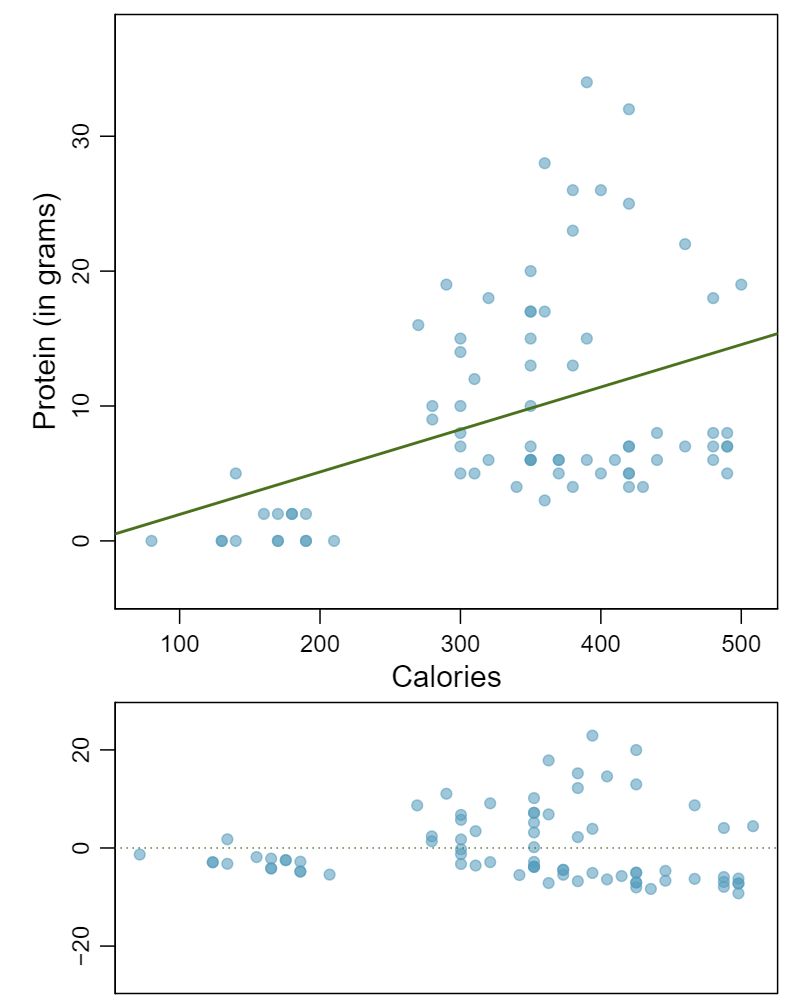
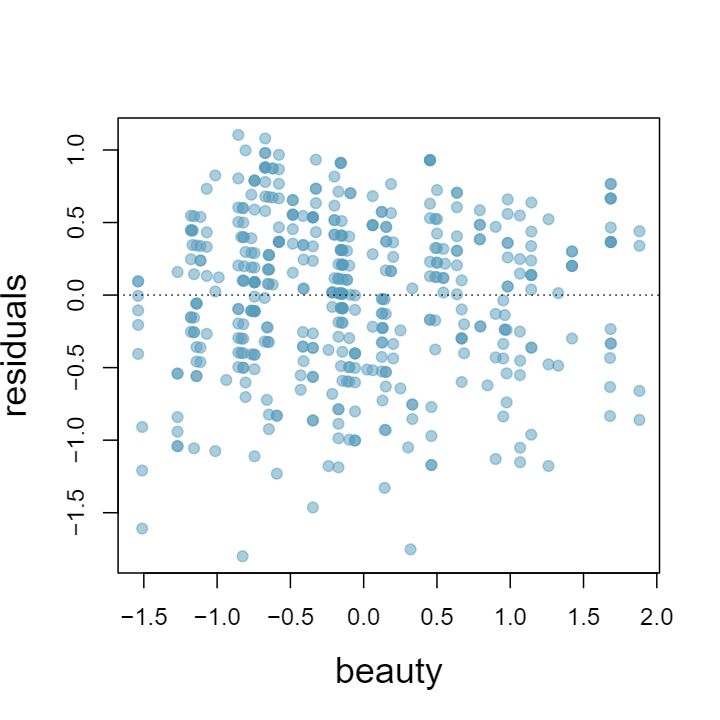
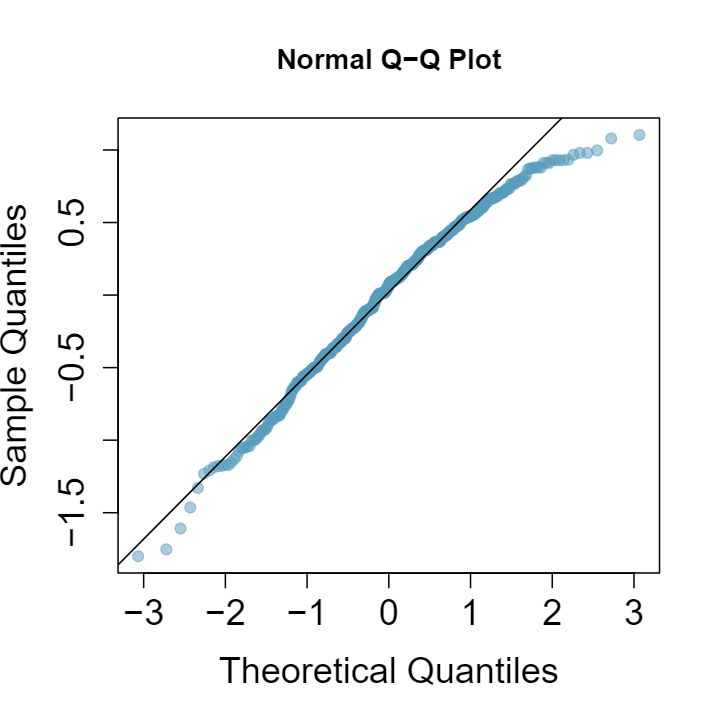
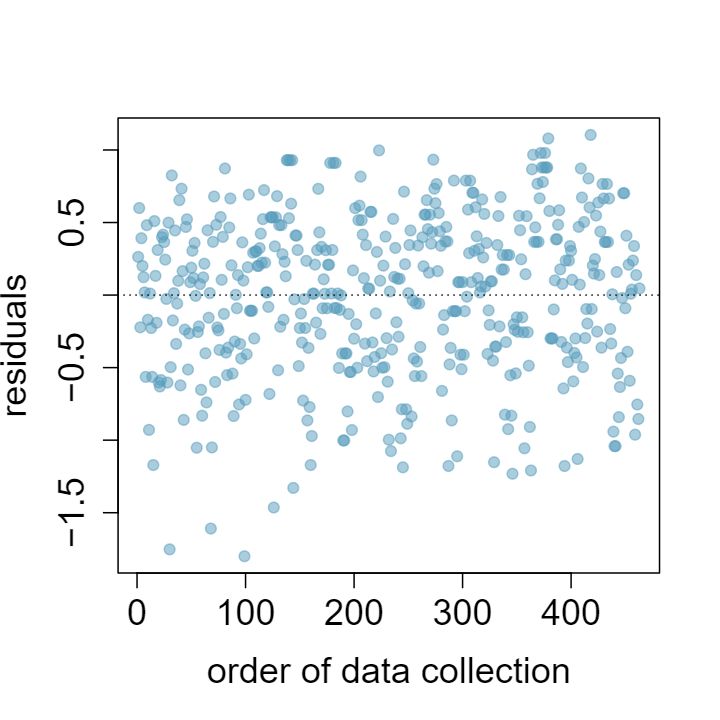
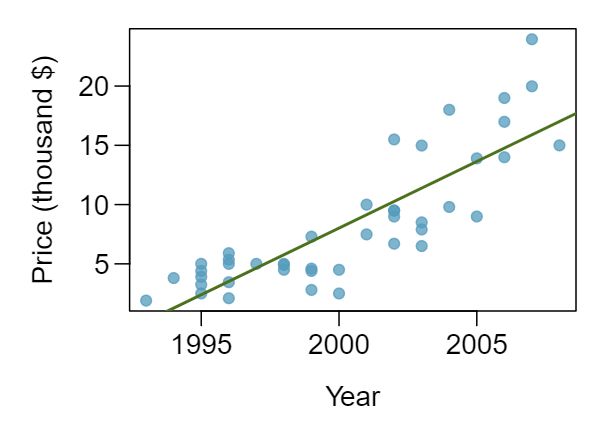
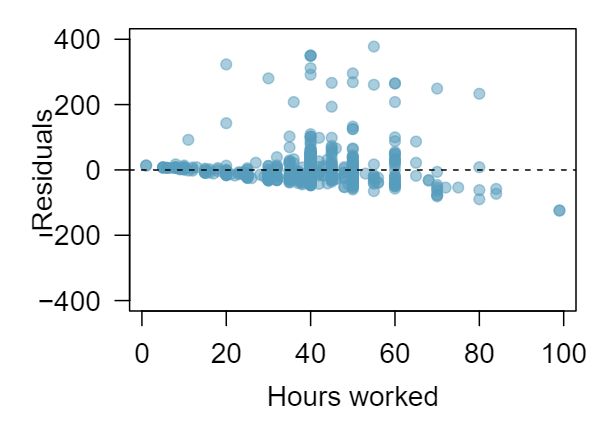
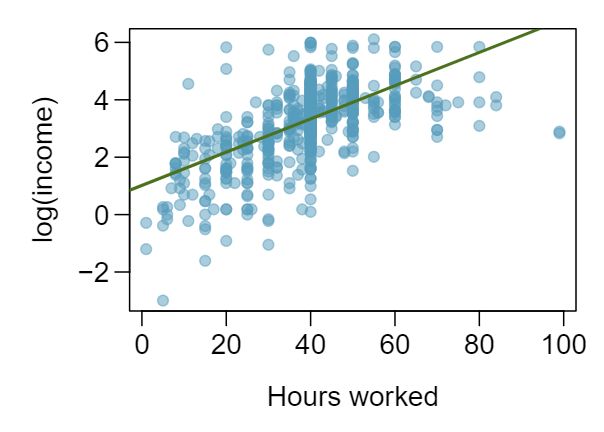
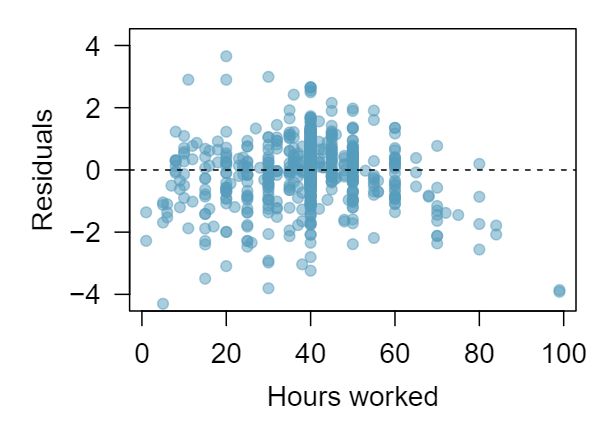
1 Visualize the residuals

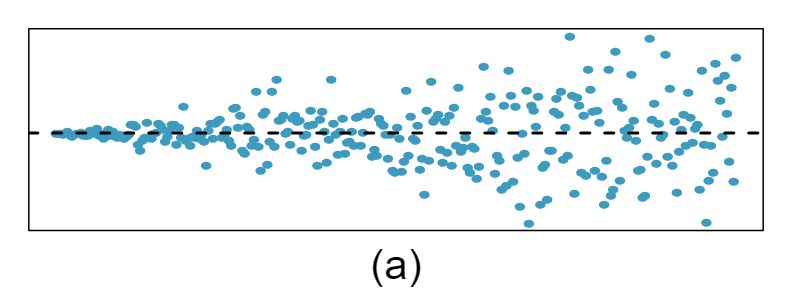
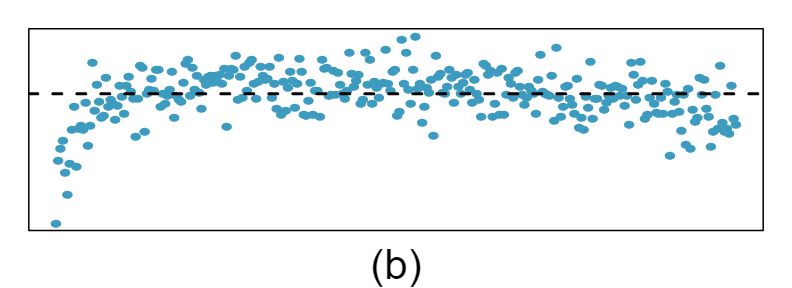
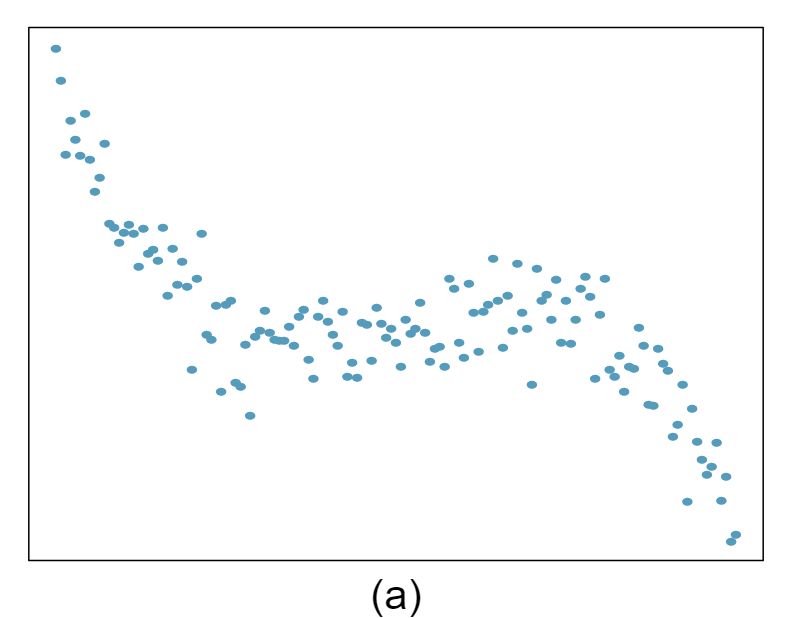
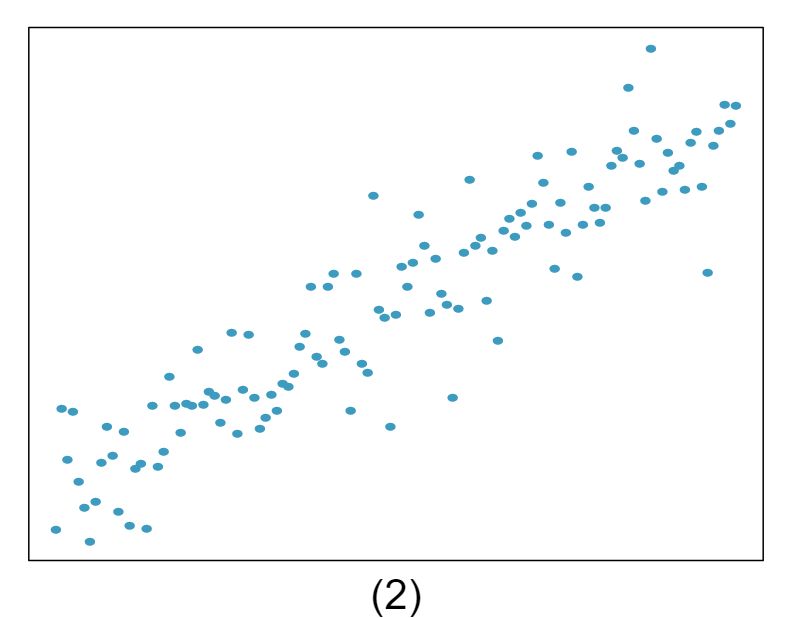
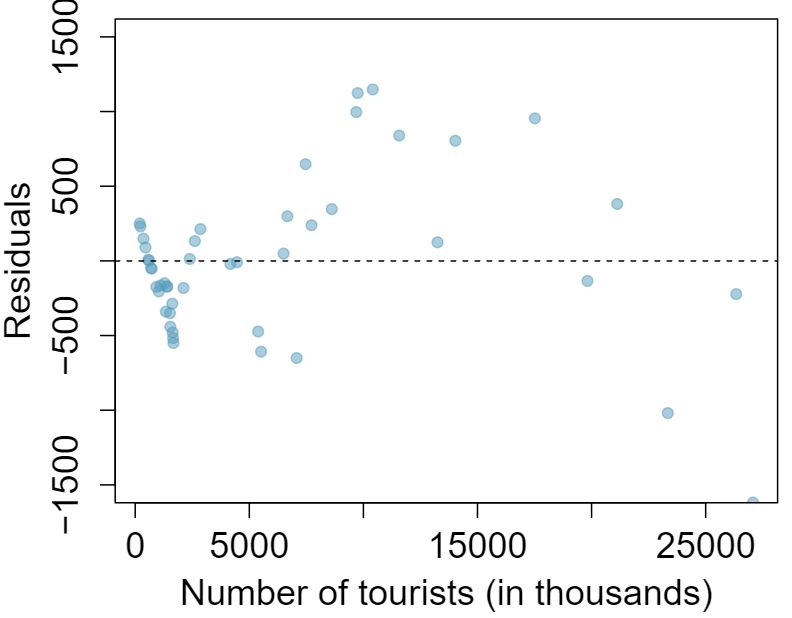
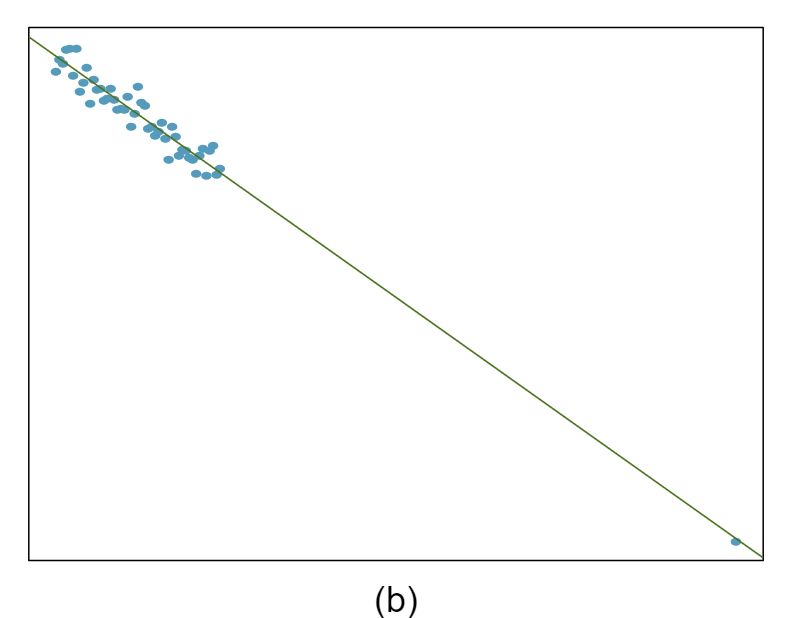
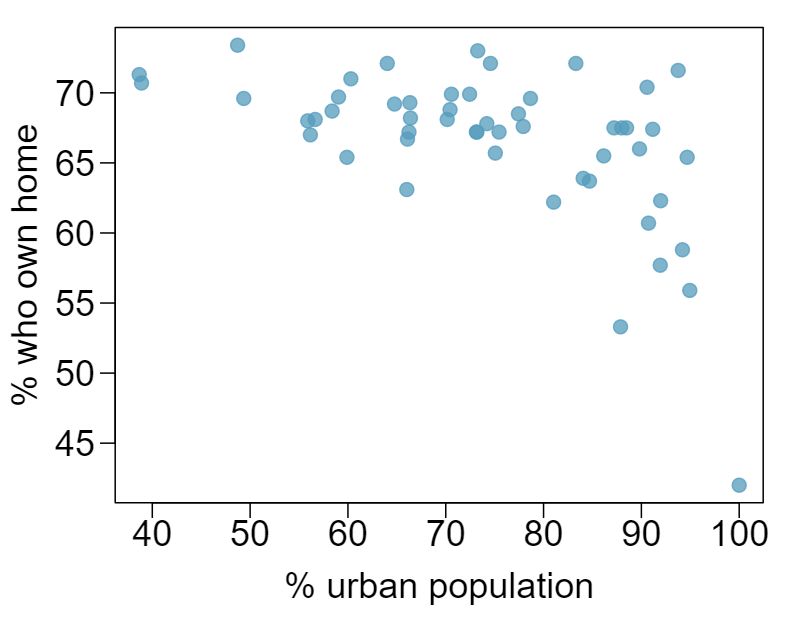
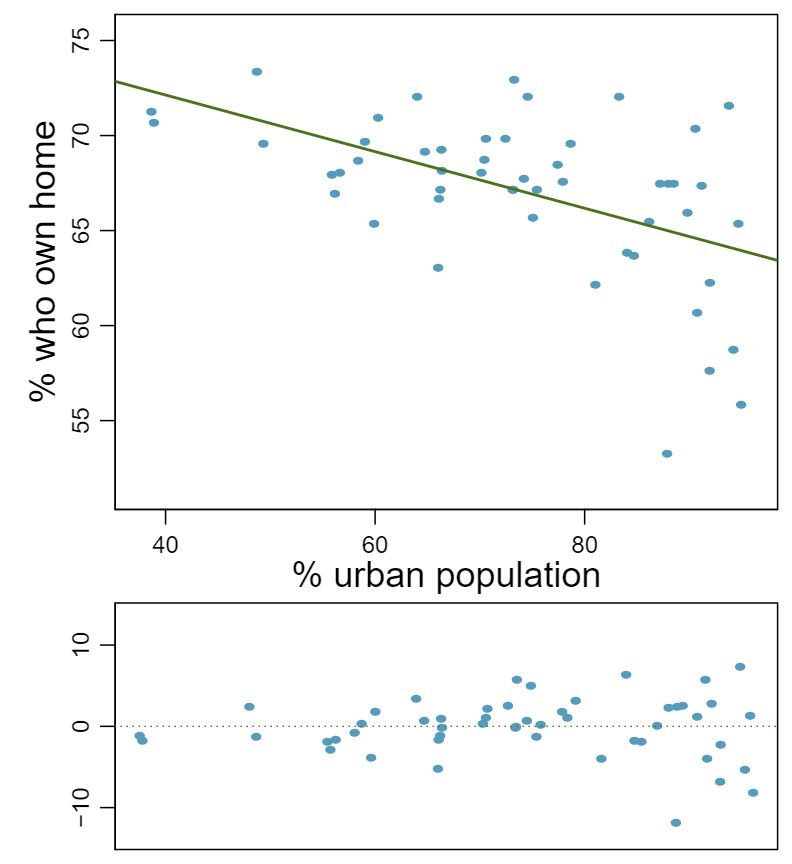
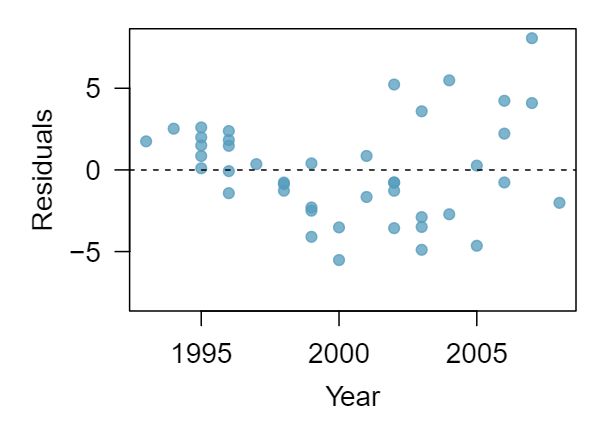
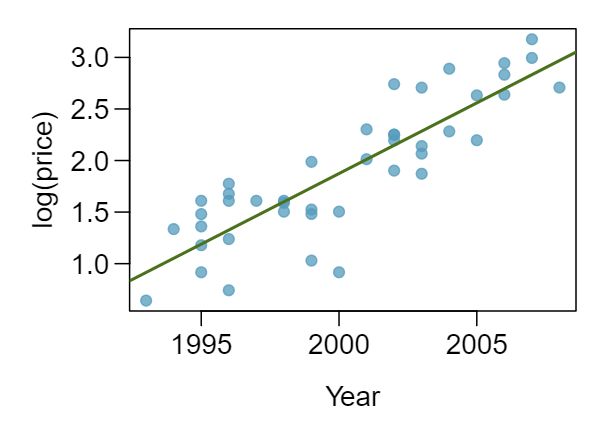
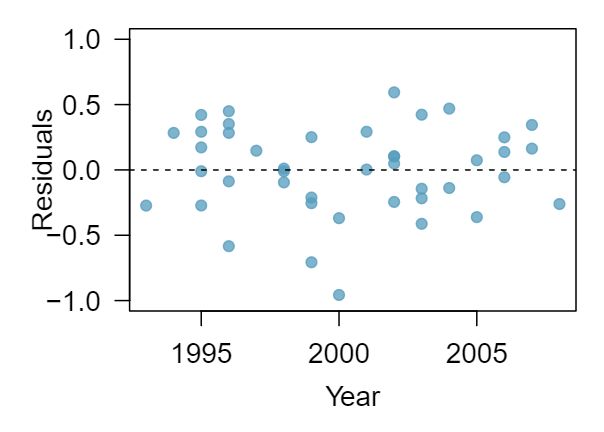
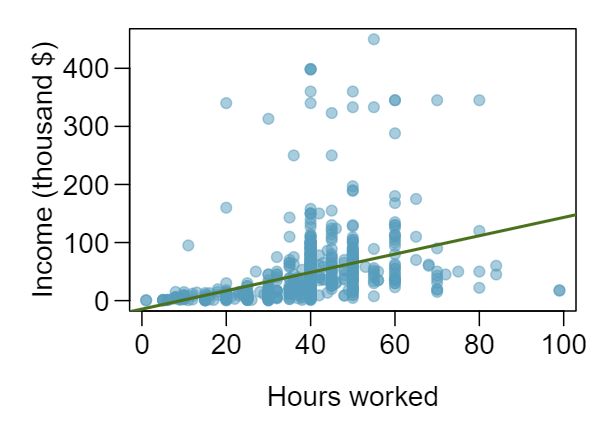
The scatterplots shown below each have a superimposed regression line. If we were to construct a residual plot (residuals versus \(x\)) for each, describe what those plots would look like.

2 Trends in the residuals

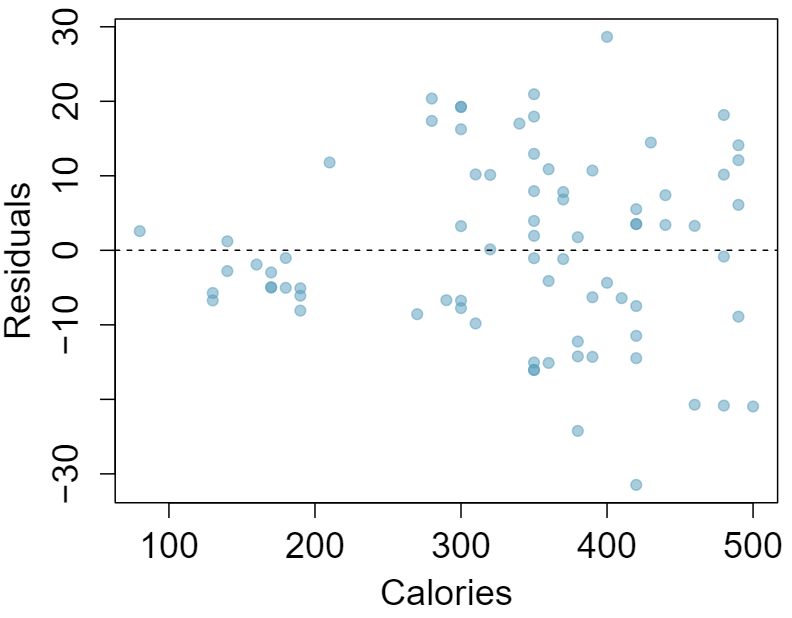
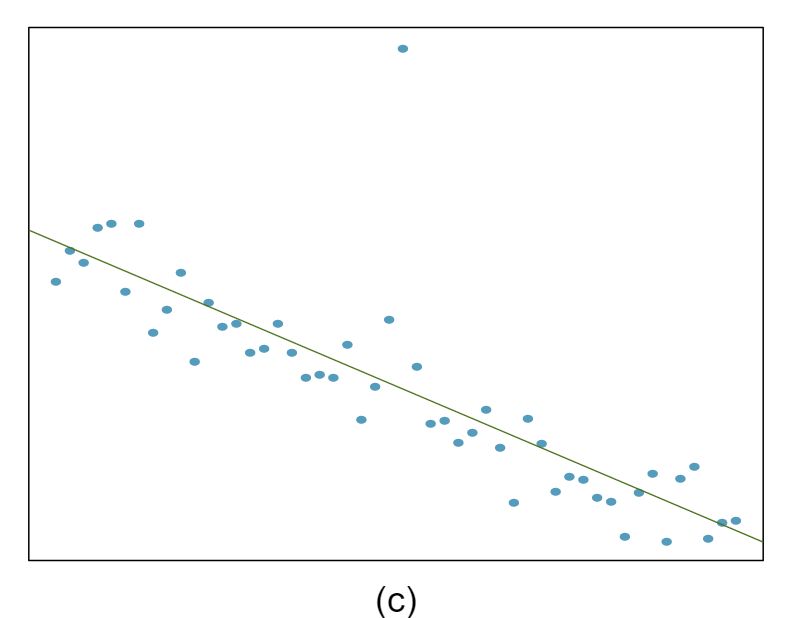
Shown below are two plots of residuals remaining after fitting a linear model to two different sets of data. Describe important features and determine if a linear model would be appropriate for these data. Explain your reasoning.

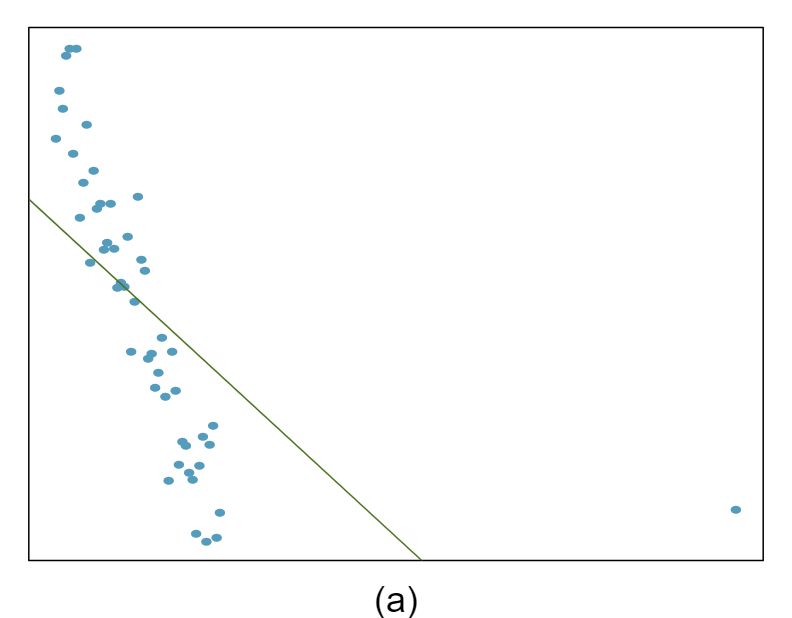
3 Identify relationships, Part I

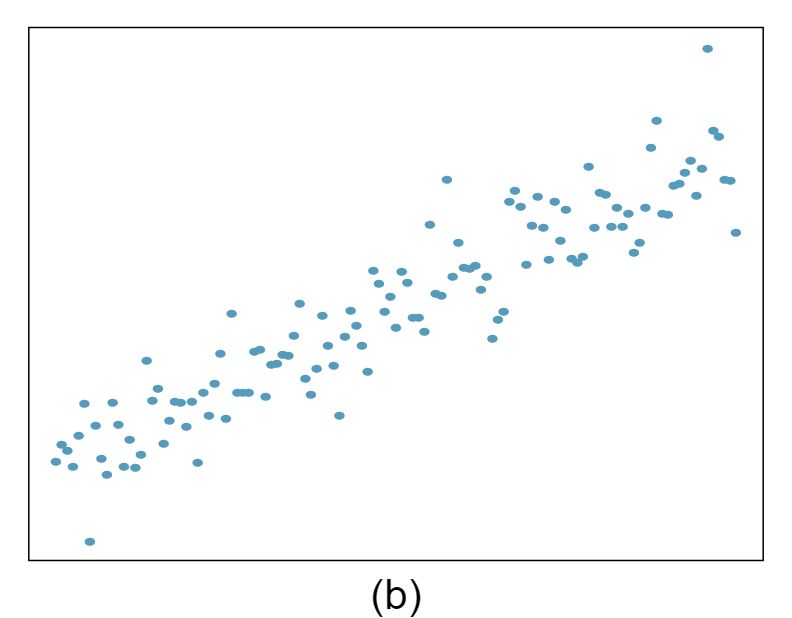
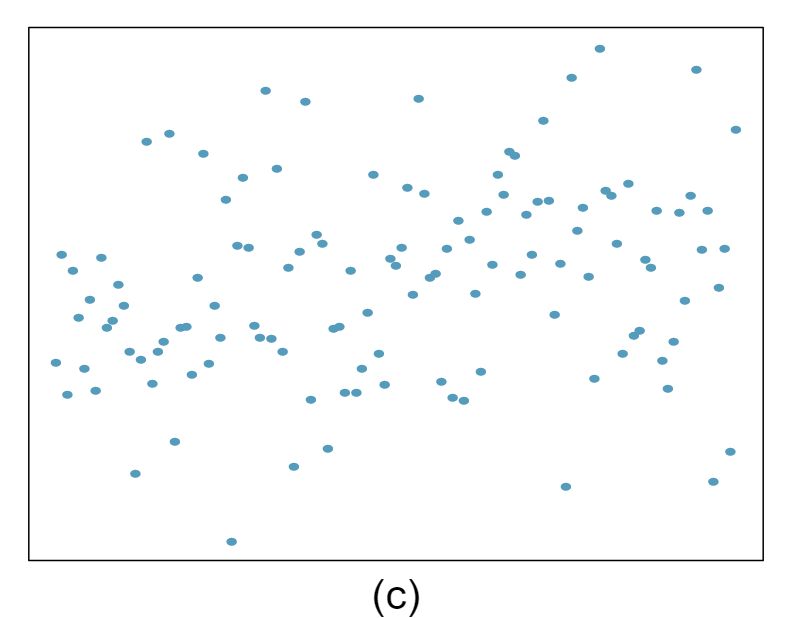
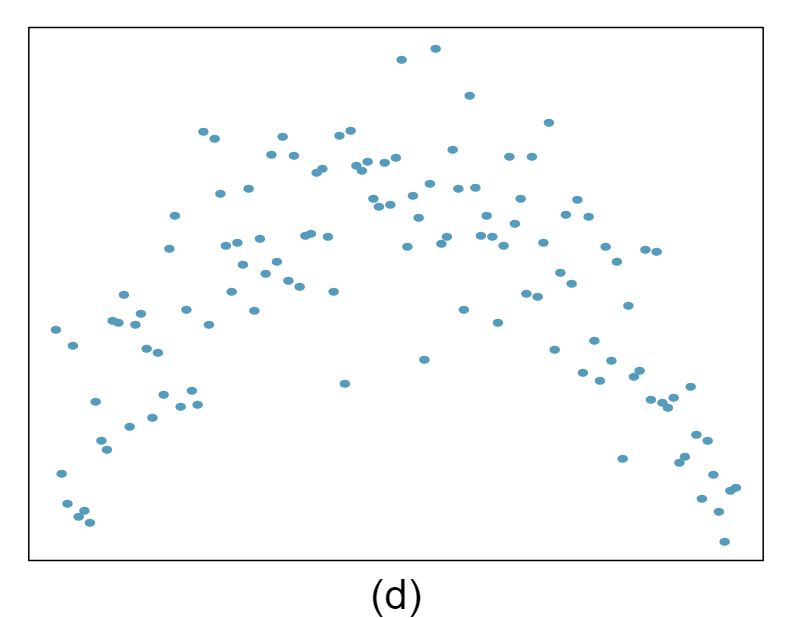
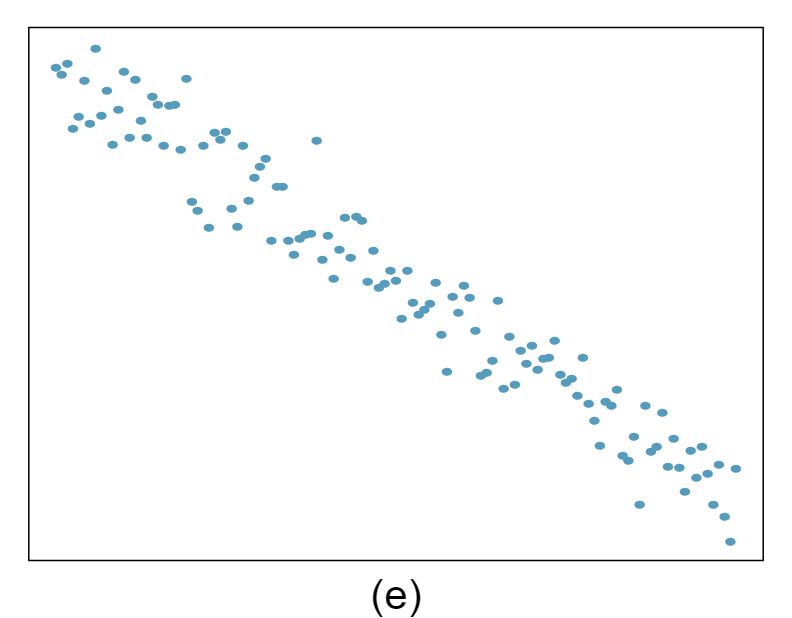
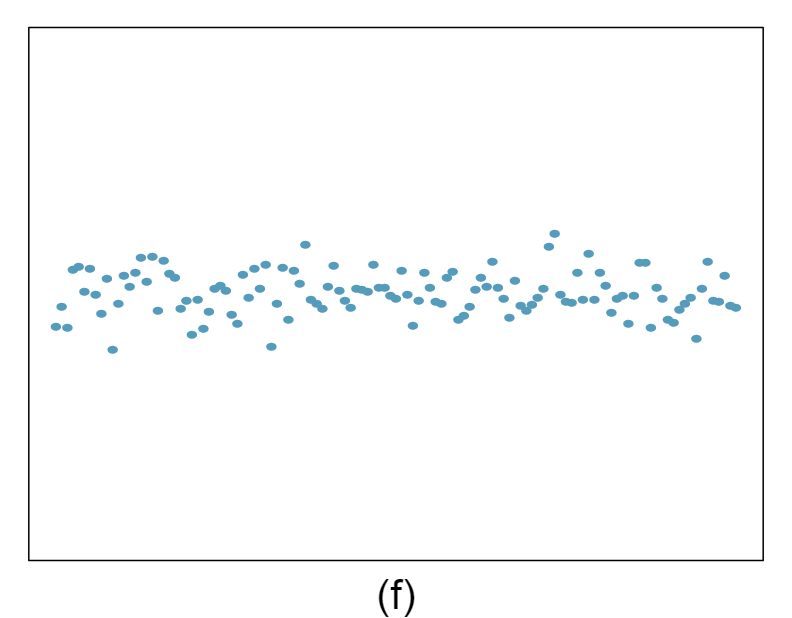
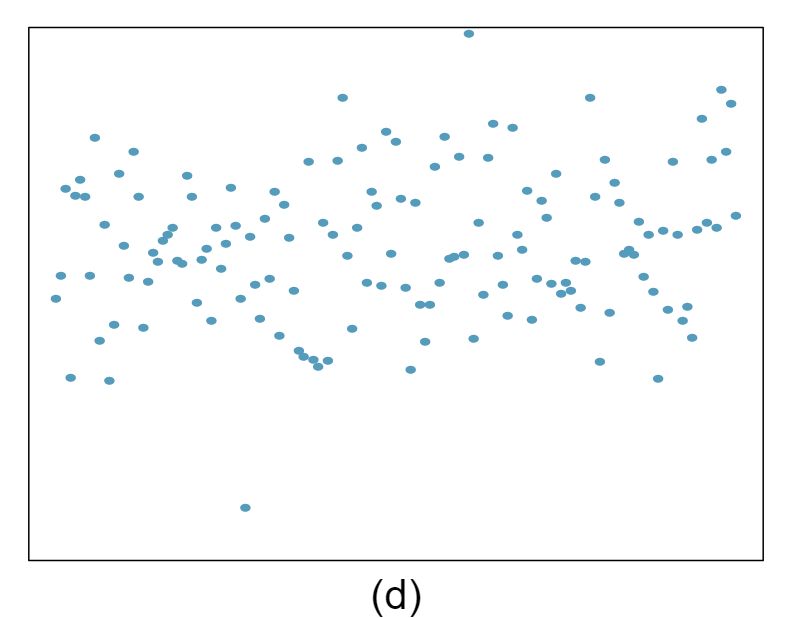
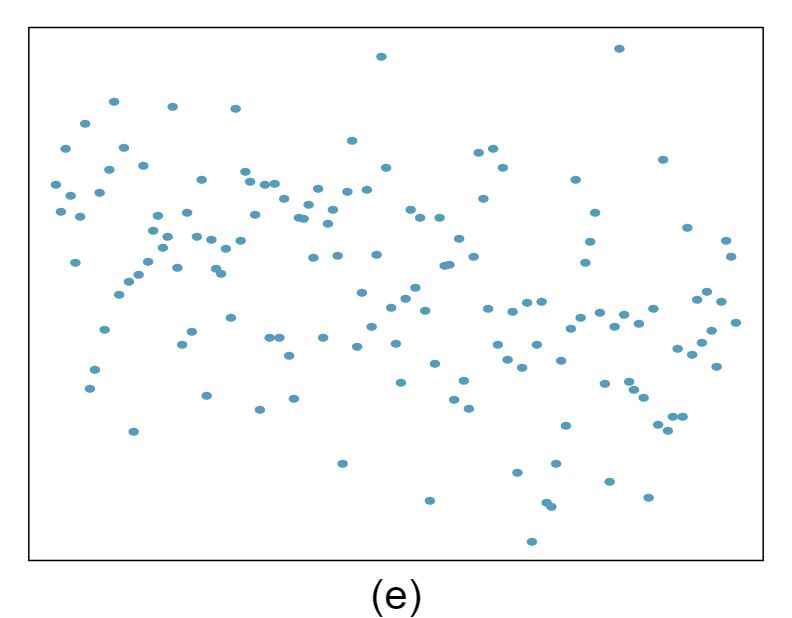
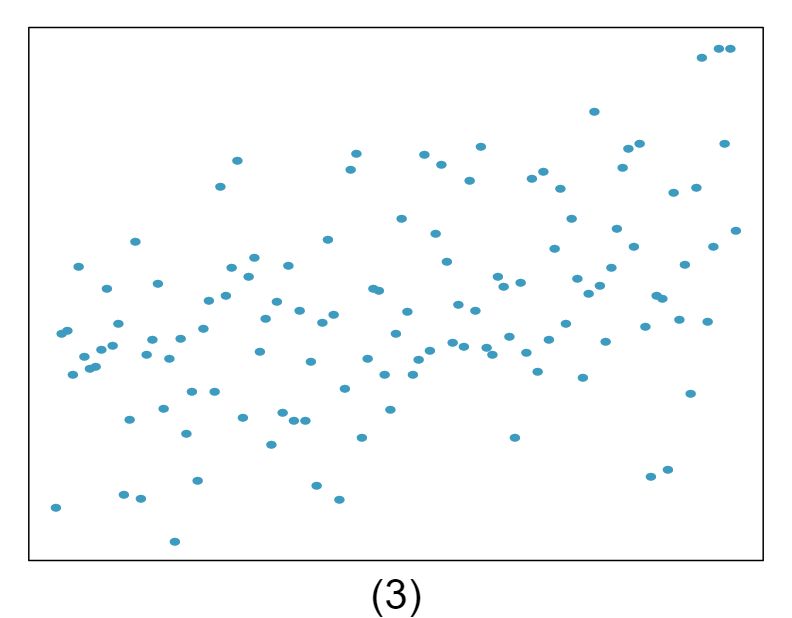
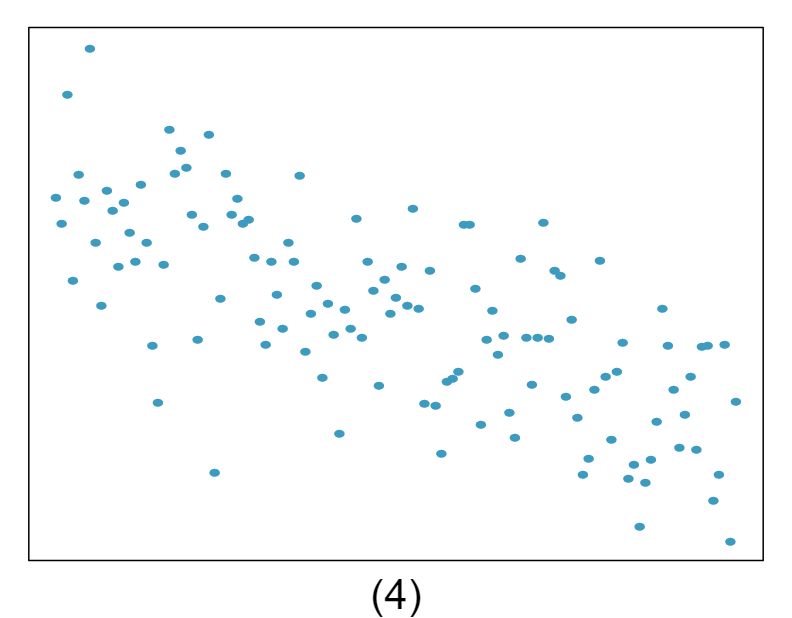
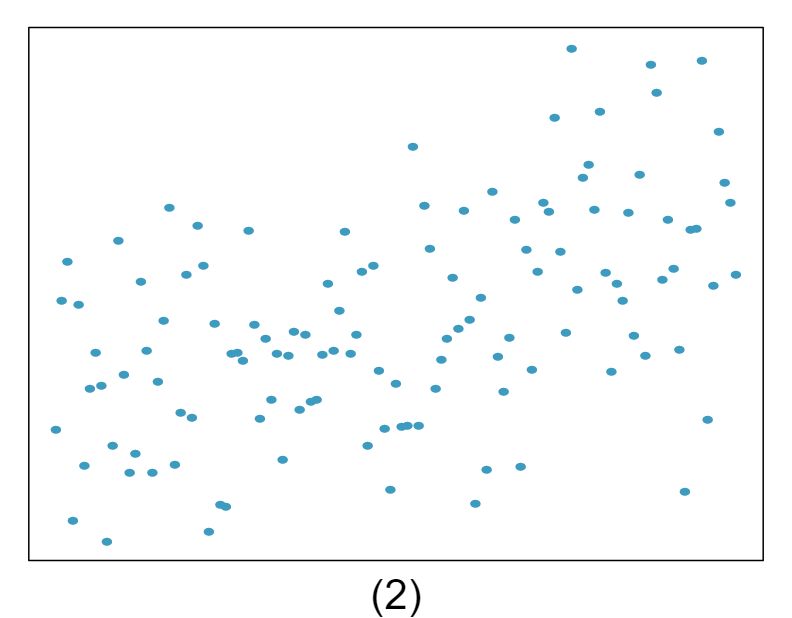
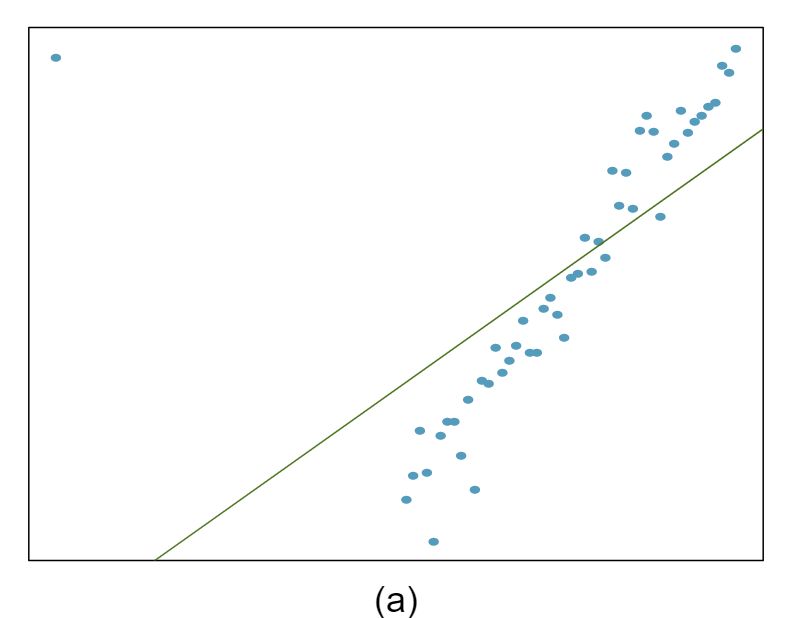
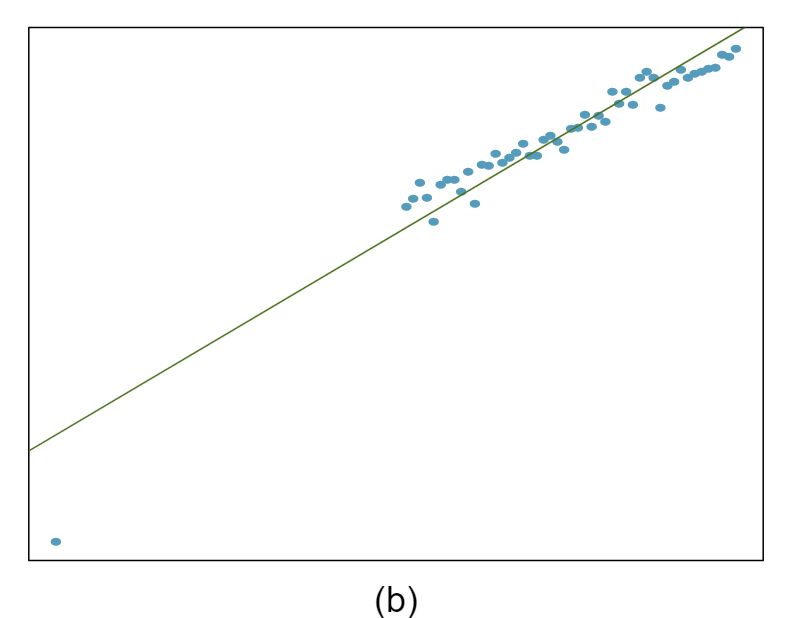
For each of the six plots, identify the strength of the relationship (e.g. weak, moderate, or strong) in the data and whether fitting a linear model would be reasonable.

4 Identify relationships, Part II

For each of the six plots, identify the strength of the relationship (e.g. weak, moderate, or strong) in the data and whether fitting a linear model would be reasonable.

5 Exams and grades

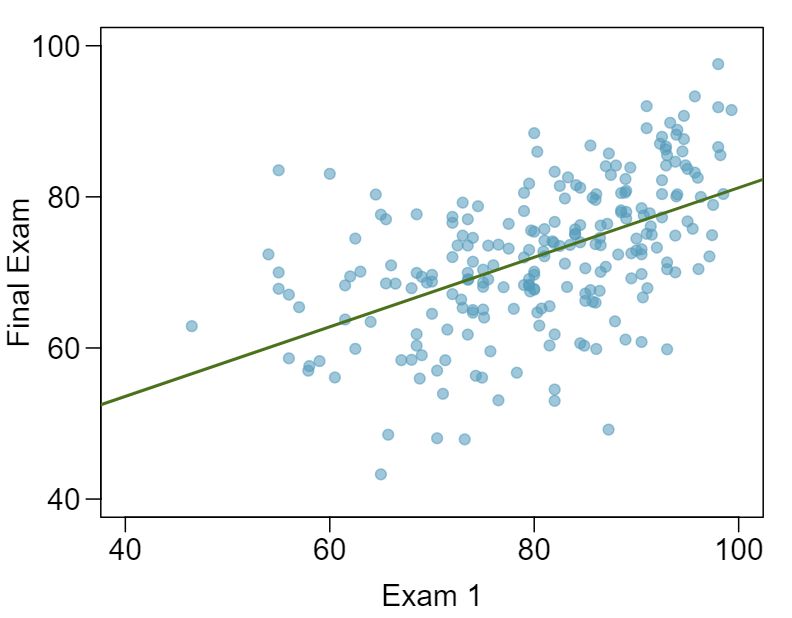
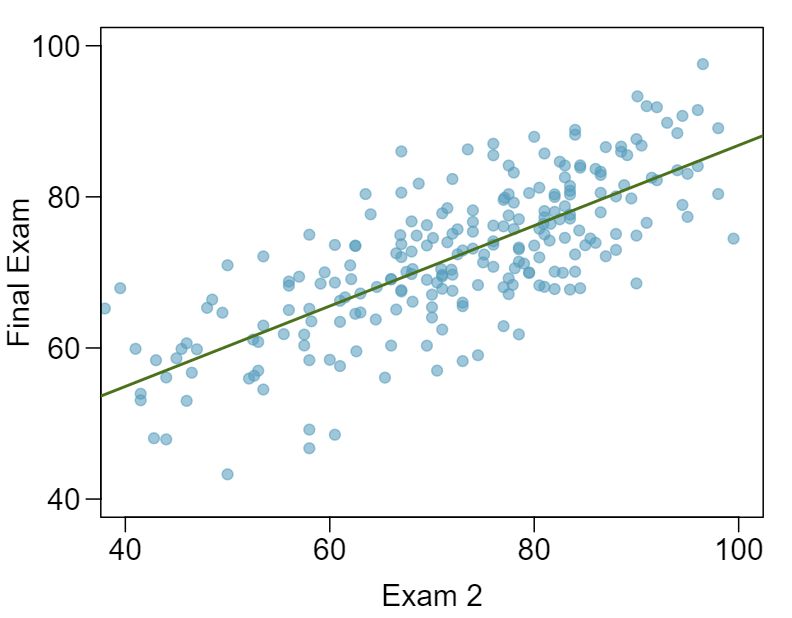
The two scatterplots below show the relationship between final and mid-semester exam grades recorded during several years for a Statistics course at a university.

1. Based on these graphs, which of the two exams has the strongest correlation with the final exam grade? Explain. Answer

   Exam 2 since there is less of a scatter in the plot of final exam grade versus exam 2. Notice that the relationship between Exam 1 and the Final Exam appears to be slightly nonlinear.

2. Can you think of a reason why the correlation between the exam you chose in part (a) and the final exam is higher? Answer

   Exam 2 and the final are relatively close to each other chronologically, or Exam 2 may be cumulative so has greater similarities in material to the final exam. Answers may vary for part (b).

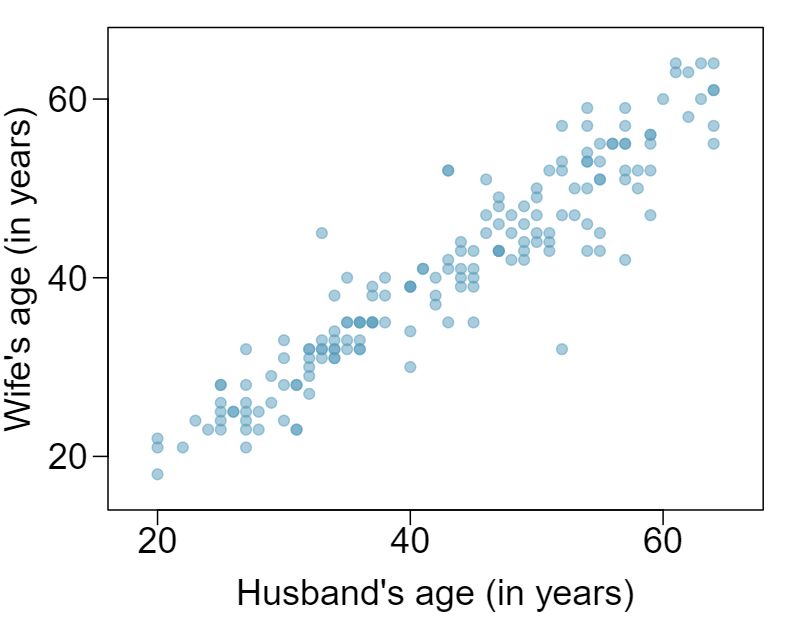
6 Husbands and wives, Part I

The Great Britain Office of Population Census and Surveys once collected data on a random sample of 170 married couples in Britain, recording the age (in years) and heights (converted here to inches) of the husbands and wives.¹D.J. Hand. A handbook of small data sets. Chapman & Hall/CRC, 1994. The first scatterplot shows the wife's age plotted against her husband's age, and the second plot shows wife's height plotted against husband's height.

1. Describe the relationship between husbands' and wives' ages.

2. Describe the relationship between husbands' and wives' heights.

3. Which plot shows a stronger correlation? Explain your reasoning.

4. Data on heights were originally collected in centimeters, and then converted to inches. Does this conversion affect the correlation between husbands' and wives' heights?

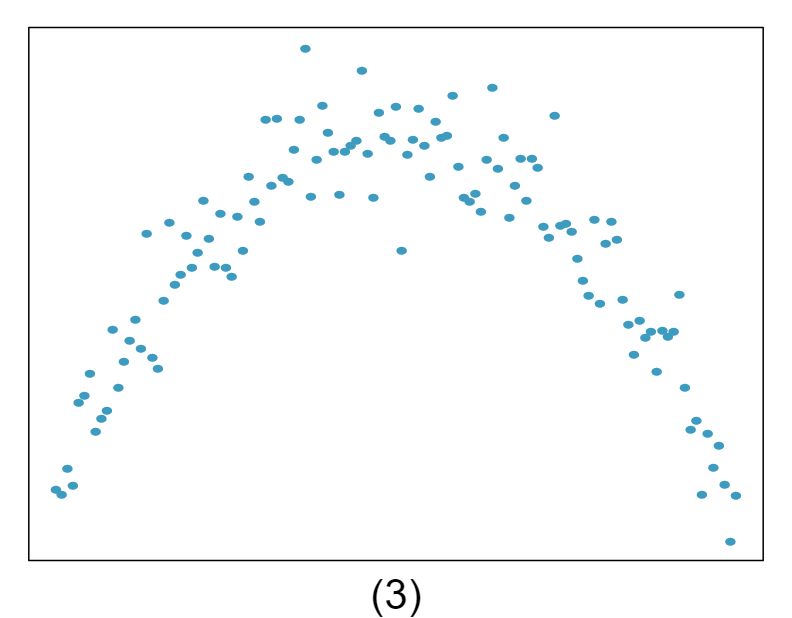
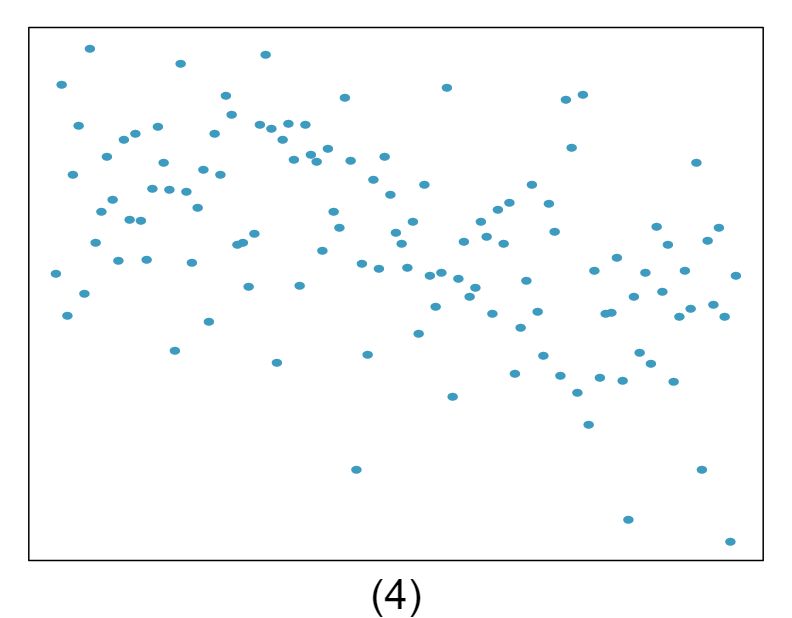
7 Match the correlation, Part I

Match the calculated correlations to the corresponding scatterplot.

1. \(r = -0.7\) Answer

   \(r = -0.7\) \(\rightarrow\) (4).

2. \(r = 0.45\) Answer

   \(r = 0.45\) \(\rightarrow\) (3).

3. \(r = 0.06\) Answer

   \(r = 0.06\) \(\rightarrow\) (1).

4. \(r = 0.92\) Answer

   \(r = 0.92\) \(\rightarrow\) (2).

8 Match the correlation, Part II

Match the calculated correlations to the corresponding scatterplot.

1. \(r = 0.49\)

2. \(r = -0.48\)

3. \(r = -0.03\)

4. \(r = -0.85\)

9 True / False

Determine if the following statements are true or false. If false, explain why.

1. A correlation coefficient of -0.90 indicates a stronger linear relationship than a correlation coefficient of 0.5. Answer

   True.

2. Correlation is a measure of the association between any two variables. Answer

   False, correlation is a measure of the linear association between any two numerical variables.

10 Guess the correlation

Eduardo and Rosie are both collecting data on number of rainy days in a year and the total rainfall for the year. Eduardo records rainfall in inches and Rosie in centimeters. How will their correlation coefficients compare?

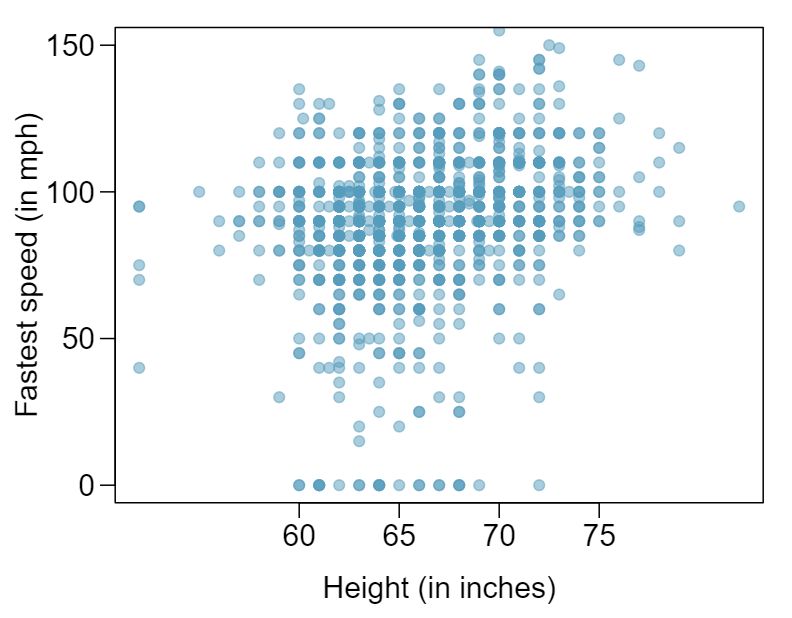
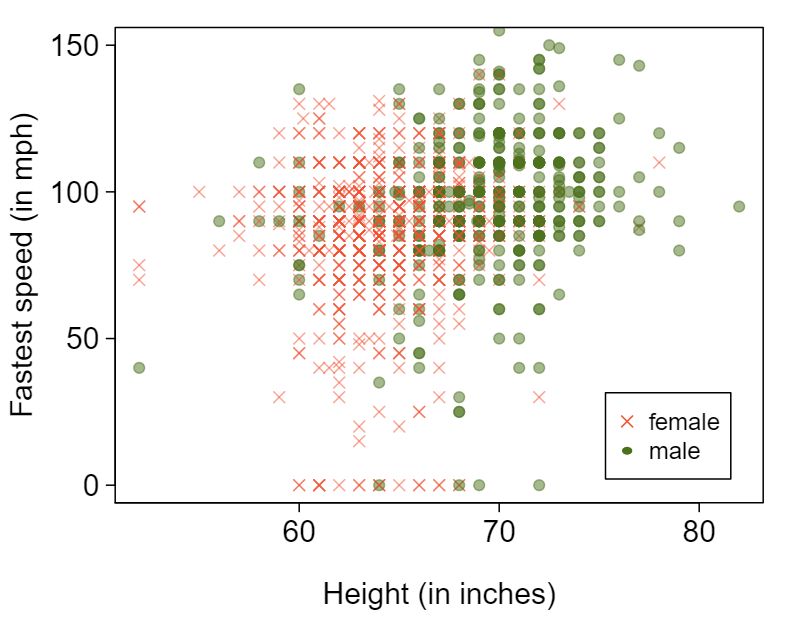
11 Speed and height

1,302 UCLA students were asked to fill out a survey where they were asked about their height, fastest speed they have ever driven, and gender. The first scatterplot displays the relationship between height and fastest speed, and the second scatterplot displays the breakdown by gender in this relationship.

1. Describe the relationship between height and fastest speed. Answer

   The relationship is positive, weak, and possibly linear. However, there do appear to be some anomalous observations along the left where several students have the same height that is notably far from the cloud of the other points. Additionally, there are many students who appear not to have driven a car, and they are represented by a set of points along the bottom of the scatterplot.

2. Why do you think these variables are positively associated? Answer

   There is no obvious explanation why simply being tall should lead a person to drive faster. However, one confounding factor is gender. Males tend to be taller than females on average, and personal experiences (anecdotal) may suggest they drive faster. If we were to follow-up on this suspicion, we would find that sociological studies confirm this suspicion.

3. What role does gender play in the relationship between height and fastest driving speed? Answer

   Males are taller on average and they drive faster. The gender variable is indeed an important confounding variable.

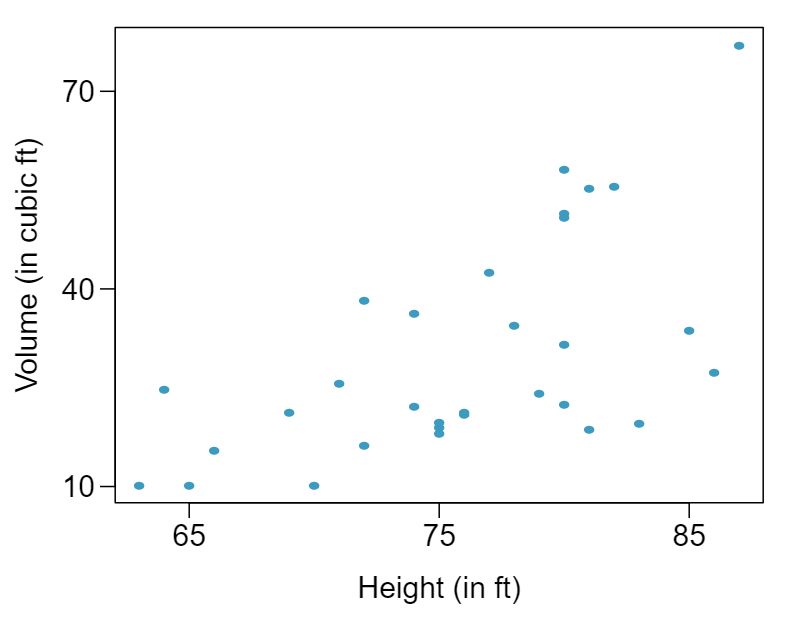
12 Trees

The scatterplots below show the relationship between height, diameter, and volume of timber in 31 felled black cherry trees. The diameter of the tree is measured 4.5 feet above the ground.²Source: R Data Set,http://stat.ethz.ch/R-manual/R-patched/library/datasets/html/trees.html

1. Describe the relationship between volume and height of these trees.

2. Describe the relationship between volume and diameter of these trees.

3. Suppose you have height and diameter measurements for another black cherry tree. Which of these variables would be preferable to use to predict the volume of timber in this tree using a simple linear regression model? Explain your reasoning.

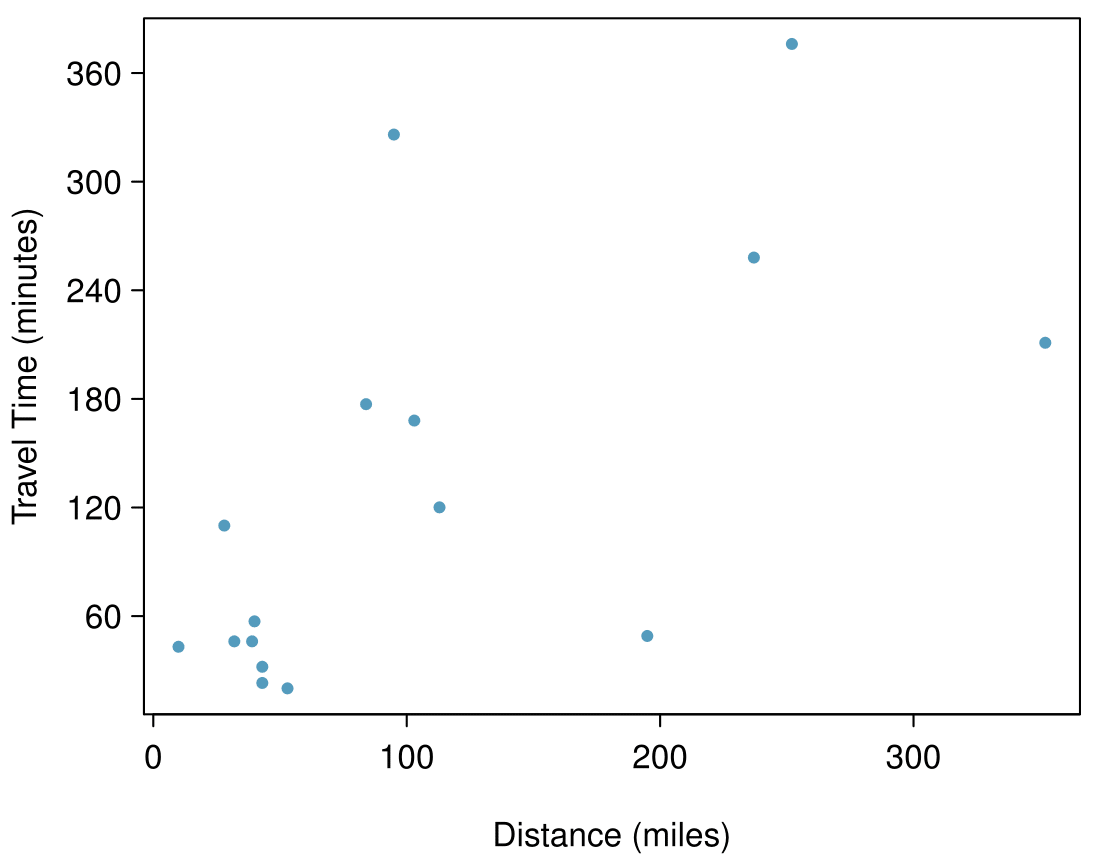
13 The Coast Starlight, Part I

The Coast Starlight Amtrak train runs from Seattle to Los Angeles. The scatterplot below displays the distance between each stop (in miles) and the amount of time it takes to travel from one stop to another (in minutes).

1. Describe the relationship between distance and travel time. Answer

   There is a somewhat weak, positive, possibly linear relationship between the distance traveled and travel time. There is clustering near the lower left corner that we should take special note of.

2. How would the relationship change if travel time was instead measured in hours, and distance was instead measured in kilometers? Answer

   Changing the units will not change the form, direction or strength of the relationship between the two variables. If longer distances measured in miles are associated with longer travel time measured in minutes, longer distances measured in kilometers will be associated with longer travel time measured in hours

3. Correlation between travel time (in miles) and distance (in minutes) is \(r = 0.636\text{.}\) What is the correlation between travel time (in kilometers) and distance (in hours)? Answer

   Changing units doesn't affect correlation: \(r = 0.636\text{.}\)

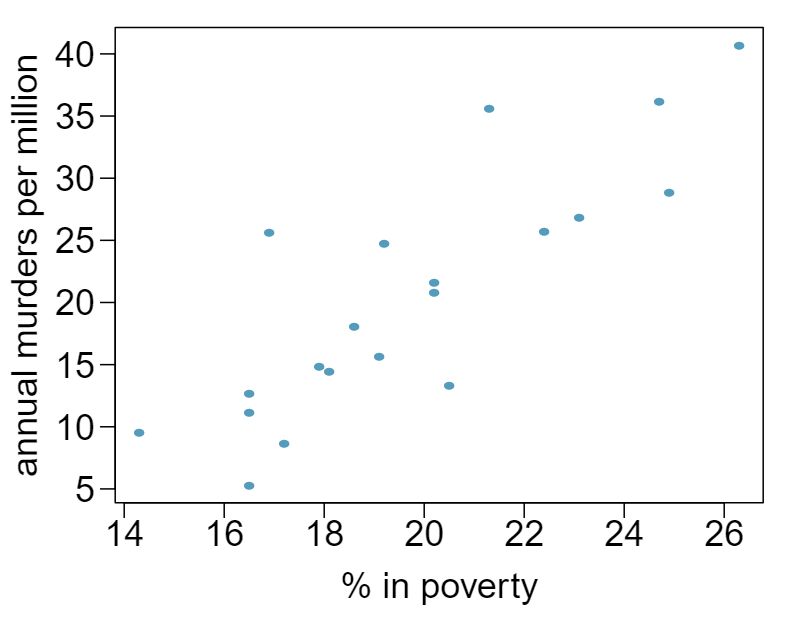
14 Crawling babies, Part I

A study conducted at the University of Denver investigated whether babies take longer to learn to crawl in cold months, when they are often bundled in clothes that restrict their movement, than in warmer months.³J.B. Benson. “Season of birth and onset of locomotion: Theoretical and methodological implications”. In: Infant behavior and development16.1 (1993), pp. 69-81. issn: 0163-6383 Infants born during the study year were split into twelve groups, one for each birth month. We consider the average crawling age of babies in each group against the average temperature when the babies are six months old (that's when babies often begin trying to crawl). Temperature is measured in degrees Fahrenheit°F and age is measured in weeks.

1. Describe the relationship between temperature and crawling age.

2. How would the relationship change if temperature was measured in degrees Celsius and age was measured in months?

3. The correlation between temperature in °F and age in weeks was \(r=-0.70\text{.}\) If we converted the temperature to  °F and age to months, what would the correlation be?

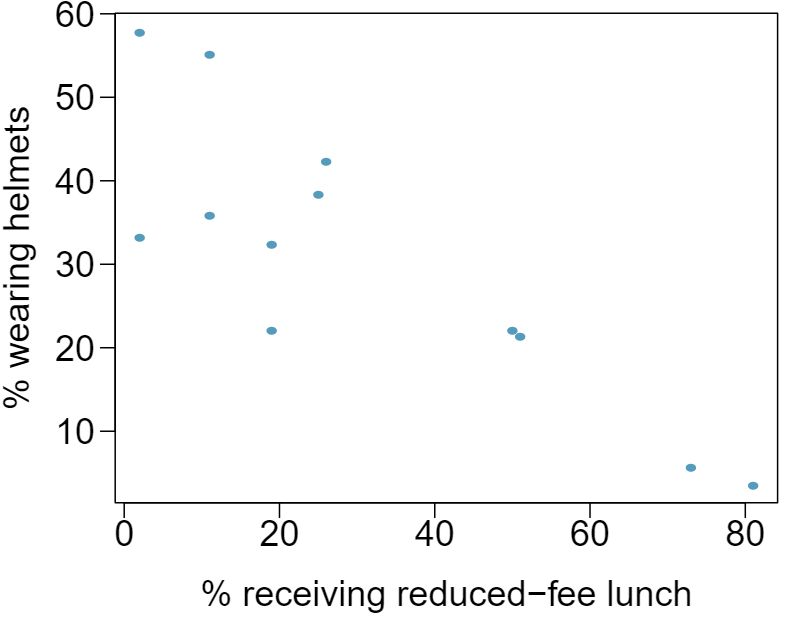
15 Body measurements, Part I

Researchers studying anthropometry collected body girth measurements and skeletal diameter measurements, as well as age, weight, height and gender for 507 physically active individuals.⁴G. Heinz et al. “Exploring relationships in body dimensions” In: Journal of Statistics Education 11.2 (2003). The scatterplot below shows the relationship between height and shoulder girth (over deltoid muscles), both measured in centimeters.

1. Describe the relationship between shoulder girth and height. Answer

   There is a moderate, positive, and linear relationship between shoulder girth and height.

2. How would the relationship change if shoulder girth was measured in inches while the units of height remained in centimeters? Answer

   Changing the units, even if just for one of the variables, will not change the form, direction or strength of the relationship between the two variables.

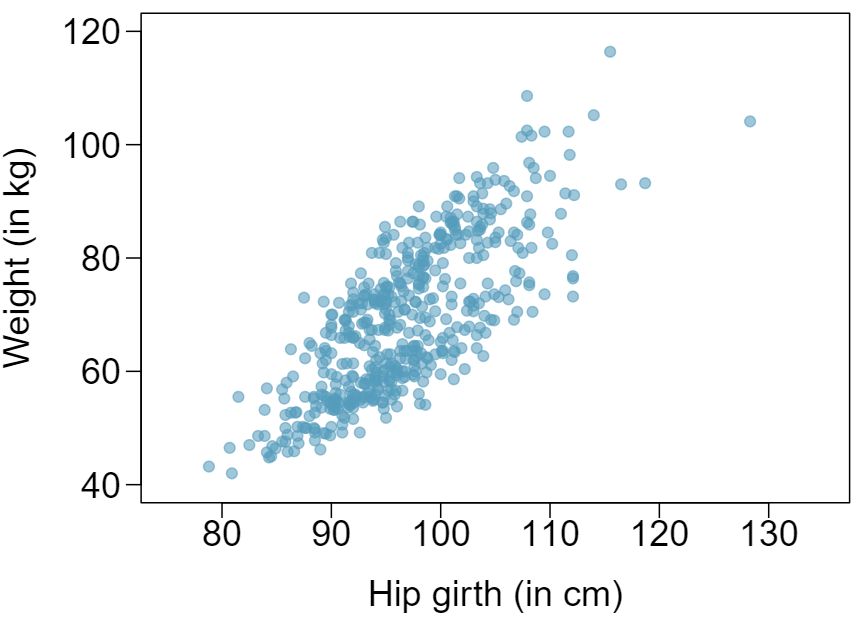
16 Body measurements, Part II

The scatterplot below shows the relationship between weight measured in kilograms and hip girth measured in centimeters from the data described in Exercise 8.6.15.

1. Describe the relationship between hip girth and weight.

2. How would the relationship change if weight was measured in pounds while the units for hip girth remained in centimeters?

17 Correlation, Part I

What would be the correlation between the ages of husbands and wives if men always married woman who were

1. 3 years younger than themselves? Answer

   In each part, we may write the husband ages as a linear function of the wife ages:\(age_{H} = age_{W} + 3\)

2. 2 years older than themselves? Answer

   In each part, we may write the husband ages as a linear function of the wife ages: \(age_{H} = age_{W} - 2\)

3. half as old as themselves? Answer

   In each part, we may write the husband ages as a linear function of the wife ages:\(age_{H} = 2 \times age_{W}\text{.}\) Since the slopes are positive and these are perfect linear relationships, the correlation will be exactly 1 in all three parts. An alternative way to gain insight into this solution is to create a mock data set, such as a data set of 5 women with ages 26, 27, 28, 29, and 30 (or some other set of ages). Then, based on the description, say for part (a), we can compute their husbands' ages as 29, 30, 31, 32, and 33. We can plot these points to see they fall on a straight line, and they always will. The same approach can be applied to the other parts as well.

18 Correlation, Part II

What would be the correlation between the annual salaries of males and females at a company if for a certain type of position men always made

1. $5,000 more than women?

2. 25% more than women?

3. 15% less than women?

19 Units of regression

Consider a regression predicting weight (kg) from height (cm) for a sample of adult males. What are the units of the correlation coefficient, the intercept, and the slope?

20 Which is higher?

Determine if I or II is higher or if they are equal. Explain your reasoning.

For a regression line, the uncertainty associated with the slope estimate, \(b_1\text{,}\) is higher when

1. there is a lot of scatter around the regression line or

2. there is very little scatter around the regression line

21 Over-under, Part I

Suppose we fit a regression line to predict the shelf life of an apple based on its weight. For a particular apple, we predict the shelf life to be 4.6 days. The apple's residual is -0.6 days. Did we over or under estimate the shelf-life of the apple? Explain your reasoning.

22 Over-under, Part II

Suppose we fit a regression line to predict the number of incidents of skin cancer per 1,000 people from the number of sunny days in a year. For a particular year, we predict the incidence of skin cancer to be 1.5 per 1,000 people, and the residual for this year is 0.5. Did we over or under estimate the incidence of skin cancer? Explain your reasoning.

23 Tourism spending

The Association of Turkish Travel Agencies reports the number of foreign tourists visiting Turkey and tourist spending by year.⁵Association of Turkish Travel Agencies, Foreign Visitors Figure & Tourist Spendings By Years. Three plots are provided: scatterplot showing the relationship between these two variables along with the least squares fit, residuals plot, and histogram of residuals.

1. Describe the relationship between number of tourists and spending. Answer

   There is a positive, very strong, linear association between the number of tourists and spending.

2. What are the explanatory and response variables? Answer

   Explanatory: number of tourists (in thousands). Response: spending (in millions of US dollars).

3. Why might we want to fit a regression line to these data? Answer

   We can predict spending for a given number of tourists using a regression line. This may be useful information for determining how much the country may want to spend in advertising abroad, or to forecast expected revenues from tourism.

4. Do the data meet the conditions required for fitting a least squares line? In addition to the scatterplot, use the residual plot and histogram to answer this question. Answer

   Even though the relationship appears linear in the scatterplot, the residual plot actually shows a nonlinear relationship. This is not a contradiction: residual plots can show divergences from linearity that can be difficult to see in a scatterplot. A simple linear model is inadequate for modeling these data. It is also important to consider that these data are observed sequentially, which means there may be a hidden structure that it is not evident in the current data but that is important to consider.

24 Nutrition at Starbucks, Part I

The scatterplot below shows the relationship between the number of calories and amount of carbohydrates (in grams) Starbucks food menu items contain.⁶Source: Starbucks.com, collected on March 10, 2011,www.starbucks.com/menu/nutrition. Since Starbucks only lists the number of calories on the display items, we are interested in predicting the amount of carbs a menu item has based on its calorie content.

1. Describe the relationship between number of calories and amount of carbohydrates (in grams) that Starbucks food menu items contain.

2. In this scenario, what are the explanatory and response variables?

3. Why might we want to fit a regression line to these data?

4. Do these data meet the conditions required for fitting a least squares line?

25 The Coast Starlight, Part II

Exercise 8.6.13 introduces data on the Coast Starlight Amtrak train that runs from Seattle to Los Angeles. The mean travel time from one stop to the next on the Coast Starlight is 129 mins, with a standard deviation of 113 minutes. The mean distance traveled from one stop to the next is 108 miles with a standard deviation of 99 miles. The correlation between travel time and distance is 0.636.

1. Write the equation of the regression line for predicting travel time. Answer

   First calculate the slope: \(b_1 = R\times s_y/s_x = 0.636\times113/99 = 0.726\text{.}\) Next, make use of the fact that the regression line passes through the point \((\bar{x},\bar{y})\text{:}\) \(\bar{y} = b_0 + b_1 \times \bar{x}\text{.}\) Plug in \(\bar{x}\text{,}\) \(\bar{y}\text{,}\) and \(b_1\text{,}\) and solve for \(b_0\text{:}\) 51. Solution: \(\widehat{traveltime} = 51 + 0.726 \times distance\text{.}\)

2. Interpret the slope and the intercept in this context. Answer

   \(b_1\text{:}\) For each additional mile in distance, the model predicts an additional 0.726 minutes in travel time. \(b_0\text{:}\) When the distance traveled is 0 miles, the travel time is expected to be 51 minutes. It does not make sense to have a travel distance of 0 miles in this context. Here, the \(y\)-intercept serves only to adjust the height of the line and is meaningless by itself.

3. Calculate \(R^2\) of the regression line for predicting travel time from distance traveled for the Coast Starlight, and interpret \(R^2\) in the context of the application. Answer

   \(R^2 = 0.636^2 = 0.40\text{.}\) About 40% of the variability in travel time is accounted for by the model, i.e. explained by the distance traveled.

4. The distance between Santa Barbara and Los Angeles is 103 miles. Use the model to estimate the time it takes for the Starlight to travel between these two cities. Answer

   \(\widehat{traveltime} = 51 + 0.726 \times distance = 51 + 0.726 \times 103 \approx 126\) minutes. (Note: we should be cautious in our predictions with this model since we have not yet evaluated whether it is a well-fit model.)

5. It actually takes the Coast Starlight about 168 mins to travel from Santa Barbara to Los Angeles. Calculate the residual and explain the meaning of this residual value. Answer

   \(e_i = y_i - \hat{y}_i = 168 - 126 = 42\) minutes. A positive residual means that the model underestimates the travel time.

6. Suppose Amtrak is considering adding a stop to the Coast Starlight 500 miles away from Los Angeles. Would it be appropriate to use this linear model to predict the travel time from Los Angeles to this point? Answer

   No, this calculation would require extrapolation.

26 Body measurements, Part III

Exercise 8.6.15 introduces data on shoulder girth and height of a group of individuals. The mean shoulder girth is 107.20 cm with a standard deviation of 10.37 cm. The mean height is 171.14 cm with a standard deviation of 9.41 cm. The correlation between height and shoulder girth is 0.67.

1. Write the equation of the regression line for predicting height.

2. Interpret the slope and the intercept in this context.

3. Calculate \(R^2\) of the regression line for predicting height from shoulder girth, and interpret it in the context of the application.

4. A randomly selected student from your class has a shoulder girth of 100 cm. Predict the height of this student using the model.

5. The student from part (d) is 160 cm tall. Calculate the residual, and explain what this residual means.

6. A one year old has a shoulder girth of 56 cm. Would it be appropriate to use this linear model to predict the height of this child?

27 Nutrition at Starbucks, Part II

Exercise 8.6.24 introduced a data set on nutrition information on Starbucks food menu items. Based on the scatterplot and the residual plot provided, describe the relationship between the protein content and calories of these menu items, and determine if a simple linear model is appropriate to predict amount of protein from the number of calories.

28 Helmets and lunches

The scatterplot shows the relationship between socioeconomic status measured as the percentage of children in a neighborhood receiving reduced-fee lunches at school (lunch) and the percentage of bike riders in the neighborhood wearing helmets (helmet). The average percentage of children receiving reduced-fee lunches is 30.8% with a standard deviation of 26.7% and the average percentage of bike riders wearing helmets is 38.8% with a standard deviation of 16.9%.

1. If the \(R^2\) for the least-squares regression line for these data is \(72\%\text{,}\) what is the correlation between lunch and helmet?

2. Calculate the slope and intercept for the least-squares regression line for these data.

3. Interpret the intercept of the least-squares regression line in the context of the application.

4. Interpret the slope of the least-squares regression line in the context of the application.

5. What would the value of the residual be for a neighborhood where 40% of the children receive reduced-fee lunches and 40% of the bike riders wear helmets? Interpret the meaning of this residual in the context of the application.

29 Murders and poverty, Part I

The following regression output is for predicting annual murders per million from percentage living in poverty in a random sample of 20 metropolitan areas.

1. Write out the linear model. Answer

   \(\widehat{murder} = -29.901 + 2.559 \times poverty\)

2. Interpret the intercept. Answer

   Expected murder rate in metropolitan areas with no poverty is -29.901 per million. This is obviously not a meaningful value, it just serves to adjust the height of the regression line.

3. Interpret the slope. Answer

   For each additional percentage increase in poverty, we expect murders per million to be higher on average by 2.559.

4. Interpret \(R^2\text{.}\) Answer

   Poverty level explains 70.52% of the variability in murder rates in metropolitan areas.

5. Calculate the correlation coefficient. Answer

   \(\sqrt{0.7052} = 0.8398\)

30 Cats, Part I

The following regression output is for predicting the heart weight (in g) of cats from their body weight (in kg). The coefficients are estimated using a dataset of 144 domestic cats.

1. Write out the linear model.

2. Interpret the intercept.

3. Interpret the slope.

4. Interpret \(R^2\text{.}\)

5. Calculate the correlation coefficient.

31 Outliers, Part I

Identify the outliers in the scatterplots shown below, and determine what type of outliers they are. Explain your reasoning.

32 Outliers, Part II

Identify the outliers in the scatterplots shown below and determine what type of outliers they are. Explain your reasoning.

33 Urban homeowners, Part I

The scatterplot below shows the percent of families who own their home vs. the percent of the population living in urban areas in 2010.⁷United States Census Bureau, 2010 Census Urban and Rural Classification and Urban Area Criteria and Housing Characteristics: 2010 There are 52 observations, each corresponding to a state in the US. Puerto Rico and District of Columbia are also included.

1. Describe the relationship between the percent of families who own their home and the percent of the population living in urban areas in 2010. Answer

   There is a negative, moderate-to-strong, somewhat linear relationship between percent of families who own their home and the percent of the population living in urban areas in 2010. There is one outlier: a state where 100% of the population is urban. The variability in the percent of homeownership also increases as we move from left to right in the plot.

2. The outlier at the bottom right corner is District of Columbia, where 100% of the population is considered urban. What type of outlier is this observation? Answer

   The outlier is located in the bottom right corner, horizontally far from the center of the other points, so it is a point with high leverage. It is an influential point since excluding this point from the analysis would greatly affect the slope of the regression line.

34 Crawling babies, Part II

Exercise 8.6.14 introduces data on the average monthly temperature during the month babies first try to crawl (about 6 months after birth) and the average first crawling age for babies born in a given month. A scatterplot of these two variables reveals a potential outlying month when the average temperature is about 53°F and average crawling age is about 28.5 weeks. Does this point have high leverage? Is it an influential point?

35 Body measurements, Part IV

The scatterplot and least squares summary below show the relationship between weight measured in kilograms and height measured in centimeters of 507 physically active individuals.

1. Describe the relationship between height and weight. Answer

   The relationship is positive, moderate-to-strong, and linear. There are a few outliers but no points that appear to be influential.

2. Write the equation of the regression line. Interpret the slope and intercept in context. Answer

   \(\widehat{weight} = -105.0113 + 1.0176 \times height\text{.}\) Slope: For each additional centimeter in height, the model predicts the average weight to be 1.0176 additional kilograms (about 2.2 pounds). Intercept: People who are 0 centimeters tall are expected to weigh -105.0113 kilograms. This is obviously not possible. Here, the \(y\)-intercept serves only to adjust the height of the line and is meaningless by itself.

3. Do the data provide strong evidence that an increase in height is associated with an increase in weight? State the null and alternative hypotheses, report the p-value, and state your conclusion. Answer

   \(H_0\text{:}\) The true slope coefficient of height is zero (\(\beta_1 = 0\)). \(H_0\text{:}\) The true slope coefficient of height is greater than zero (\(\beta_1 \gt 0\)). A two-sided test would also be acceptable for this application. The p-value for the two-sided alternative hypothesis (\(\beta_1 \ne 0\)) is incredibly small, so the p-value for the one-sided hypothesis will be even smaller. That is, we reject \(H_0\text{.}\) The data provide convincing evidence that height and weight are positively correlated. The true slope parameter is indeed greater than 0.

4. The correlation coefficient for height and weight is 0.72. Calculate \(R^2\) and interpret it in context. Answer

   \(R^2 = 0.72^2 = 0.52\text{.}\) Approximately 52% of the variability in weight can be explained by the height of individuals.

36 Beer and blood alcohol content

Many people believe that gender, weight, drinking habits, and many other factors are much more important in predicting blood alcohol content (BAC) than simply considering the number of drinks a person consumed. Here we examine data from sixteen student volunteers at Ohio State University who each drank a randomly assigned number of cans of beer. These students were evenly divided between men and women, and they differed in weight and drinking habits. Thirty minutes later, a police officer measured their blood alcohol content (BAC) in grams of alcohol per deciliter of blood.⁸J. Malkevitch and L.M. Lesser. For All Practical Purposes: Mathematical Literacy in Today's World. WH Freeman & Co, 2008. The scatterplot and regression table summarize the findings.

1. Describe the relationship between the number of cans of beer and BAC.

2. Write the equation of the regression line. Interpret the slope and intercept in context.

3. Do the data provide strong evidence that drinking more cans of beer is associated with an increase in blood alcohol? State the null and alternative hypotheses, report the p-value, and state your conclusion.

4. The correlation coefficient for number of cans of beer and BAC is 0.89. Calculate \(R^2\) and interpret it in context.

5. Suppose we visit a bar, ask people how many drinks they have had, and also take their BAC. Do you think the relationship between number of drinks and BAC would be as strong as the relationship found in the Ohio State study?

37 Husbands and wives, Part II

The scatterplot below summarizes husbands' and wives' heights in a random sample of 170 married couples in Britain, where both partners' ages are below 65 years. Summary output of the least squares fit for predicting wife's height from husband's height is also provided in the table.

1. Is there strong evidence that taller men marry taller women? State the hypotheses and include any information used to conduct the test. Answer

   \(H_0\text{:}\) \(\beta_1 = 0\text{.}\) \(H_A\text{:}\) \(\beta_1 \gt 0\text{.}\) A two-sided test would also be acceptable for this application. The p-value, as reported in the table, is incredibly small. Thus, for a one-sided test, the p-value will also be incredibly small, and we reject \(H_0\text{.}\) The data provide convincing evidence that wives' and husbands' heights are positively correlated.

2. Write the equation of the regression line for predicting wife's height from husband's height. Answer

   \(\widehat{height}_{W} = 43.5755 + 0.2863 \times height_{H}\text{.}\)

3. Interpret the slope and intercept in the context of the application. Answer

   Slope: For each additional inch in husband's height, the average wife's height is expected to be an additional 0.2863 inches on average. Intercept: Men who are 0 inches tall are expected to have wives who are, on average, 43.5755 inches tall. The intercept here is meaningless, and it serves only to adjust the height of the line.

4. Given that \(R^2 = 0.09\text{,}\) what is the correlation of heights in this data set? Answer

   The slope is positive, so \(r\) must also be positive. \(r = \sqrt{0.09} = 0.30\text{.}\)

5. You meet a married man from Britain who is 5'9" (69 inches). What would you predict his wife's height to be? How reliable is this prediction? Answer

   63.2612. Since \(R^2\) is low, the prediction based on this regression model is not very reliable.

6. You meet another married man from Britain who is 6'7" (79 inches). Would it be wise to use the same linear model to predict his wife's height? Why or why not? Answer

   No, we should avoid extrapolating.

38 Husbands and wives, Part III

Exercise 8.6.6 presents a scatterplot displaying the relationship between husbands' and wives' ages in a random sample of 170 married couples in Britain, where both partners' ages are below 65 years. Given below is summary output of the least squares fit for predicting wife's age from husband's age.

1. We might wonder, is the age difference between husbands and wives consistent across ages? If this were the case, then the slope parameter would be \(\beta_1 = 1\text{.}\) Use the information above to evaluate if there is strong evidence that the difference in husband and wife ages differs for different ages.

2. Write the equation of the regression line for predicting wife's age from husband's age.

3. Interpret the slope and intercept in context.

4. Given that \(R^2 = 0.88\text{,}\) what is the correlation of ages in this data set?

5. You meet a married man from Britain who is 55 years old. What would you predict his wife's age to be? How reliable is this prediction?

6. You meet another married man from Britain who is 85 years old. Would it be wise to use the same linear model to predict his wife's age? Explain.

39 Urban homeowners, Part II

Exercise 8.6.33 gives a scatterplot displaying the relationship between the percent of families that own their home and the percent of the population living in urban areas. Below is a similar scatterplot, excluding District of Columbia, as well as the residuals plot. There were 51 cases.

1. For these data, \(R^2=0.28\text{.}\) What is the correlation? How can you tell if it is positive or negative? Answer

   \(r = \sqrt{0.28} \approx -0.53\text{,}\) we know the correlation is negative due to the negative association shown in the scatterplot.

2. Examine the residual plot. What do you observe? Is a simple least squares fit appropriate for these data? Answer

   The residuals appear to be fan shaped, indicating non-constant variance. Therefore a simple least squares fit is not appropriate for these data.

40 Rate my professor

Many college courses conclude by giving students the opportunity to evaluate the course and the instructor anonymously. However, the use of these student evaluations as an indicator of course quality and teaching effectiveness is often criticized because these measures may reflect the influence of non-teaching related characteristics, such as the physical appearance of the instructor. Researchers at University of Texas, Austin collected data on teaching evaluation score (higher score means better) and standardized beauty score (a score of 0 means average, negative score means below average, and a positive score means above average) for a sample of 463 professors.⁹Daniel S Hamermesh and Amy Parker. “Beauty in the classroom: Instructors pulchritude and putative pedagogical productivity”. In: Economics of Education Review 24.4 (2005), pp. 369-376. The scatterplot below shows the relationship between these variables, and also provided is a regression output for predicting teaching evaluation score from beauty score.

1. Given that the average standardized beauty score is -0.0883 and average teaching evaluation score is 3.9983, calculate the slope. Alternatively, the slope may be computed using just the information provided in the model summary table.

2. Do these data provide convincing evidence that the slope of the relationship between teaching evaluation and beauty is positive? Explain your reasoning.

3. List the conditions required for linear regression and check if each one is satisfied for this model based on the following diagnostic plots.

   

   
   

   

41 Murders and poverty, Part II

Exercise 8.6.29 presents regression output from a model for predicting annual murders per million from percentage living in poverty based on a random sample of 20 metropolitan areas. The model output is also provided below.

1. What are the hypotheses for evaluating whether poverty percentage is a significant predictor of murder rate? Answer

   \(H_0: \beta_1 = 0; H_A: \beta_1 \ne 0\)

2. State the conclusion of the hypothesis test from part (a) in context of the data. Answer

   The p-value for this test is approximately 0, therefore we reject \(H_0\text{.}\) The data provide convincing evidence that poverty percentage is a significant predictor of murder rate.

3. Calculate a 95% confidence interval for the slope of poverty percentage, and interpret it in context of the data. Answer

   \(n = 20, df = 18, T^*_{18} = 2.10\text{;}\) \(2.559 \pm 2.10 \times 0.390 = (1.74, 3.378)\text{;}\) For each percentage point poverty is higher, murder rate is expected to be higher on average by 1.74 to 3.378 per million.

4. Do your results from the hypothesis test and the confidence interval agree? Explain. Answer

   Yes, we rejected \(H_0\) and the confidence interval does not include 0.

42 Babies

Is the gestational age (time between conception and birth) of a low birth-weight baby useful in predicting head circumference at birth? Twenty-five low birth-weight babies were studied at a Harvard teaching hospital; the investigators calculated the regression of head circumference (measured in centimeters) against gestational age (measured in weeks). The estimated regression line is

1. What is the predicted head circumference for a baby whose gestational age is 28 weeks?

2. The standard error for the coefficient of gestational age is 0.35, which is associated with \(df=23\text{.}\) Does the model provide strong evidence that gestational age is significantly associated with head circumference?

43 Murders and poverty, Part III

In Exercise 8.6.41 you evaluated whether poverty percentage is a significant predictor of murder rate. How, if at all, would your answer change if we wanted to find out whether poverty percentage is positively associated with murder rate. Make sure to include the appropriate p-value for this hypothesis test in your answer.

44 Cats, Part II

Exercise 8.6.30 presents regression output from a model for predicting the heart weight (in g) of cats from their body weight (in kg). The coefficients are estimated using a dataset of 144 domestic cat. The model output is also provided below.

1. What are the hypotheses for evaluating whether body weight is positively associated with heart weight in cats?

2. State the conclusion of the hypothesis test from part (a) in context of the data.

3. Calculate a 95% confidence interval for the slope of body weight, and interpret it in context of the data.

4. Do your results from the hypothesis test and the confidence interval agree? Explain.

45 Used trucks

The scatterplot below shows the relationship between year and price (in thousands of $) of a random sample of 42 pickup trucks. Also shown is a residuals plot for the linear model for predicting price from year.

1. Describe the relationship between these two variables and comment on whether a linear model is appropriate for modeling the relationship between year and price. Answer

   The relationship is positive, non-linear, and somewhat strong. Due to the non-linear form of the relationship and the clear non-constant variance in the residuals, a linear model is not appropriate for modeling the relationship between year and price.

2. The scatterplot below shows the relationship between logged (natural log) price and year of these trucks, as well as the residuals plot for modeling these data. Comment on which model (linear model from earlier or logged model presented here) is a better fit for these data.
   

   
   Answer

   The logged model is a much better fit: the scatter plot shows a linear relationships and the residuals do not appear to have a pattern.

3. The output for the logged model is given below. Interpret the slope in context of the data.

   	Estimate	Std. Error	t value	Pr(\(\gt\)\(|\)t\(|\))
   (Intercept)	-271.981	25.042	-10.861	0.000
   Year	0.137	0.013	10.937	0.000

   Answer

   For each year increase in the year of the truck (for each year the truck is newer) we would expect the price of the truck to increase on average by a factor of \(e^{0.137} \approx 1.15\text{,}\) i.e. by 15%.

46 Income and hours worked

The scatterplot below shows the relationship between income and years worked for a random sample of 787 Americans. Also shown is a residuals plot for the linear model for predicting income from hours worked. The data come from the 2012 American Community Survey.¹⁰United States Census Bureau. Summary File. 2012 American Community Survey DEAD LINK. U.S. Census Bureaus American Community Survey Office, 2013. Web.

1. Describe the relationship between these two variables and comment on whether a linear model is appropriate for modeling the relationship between year and price.
2. The scatterplot below shows the relationship between logged (natural log) income and hours worked, as well as the residuals plot for modeling these data. Comment on which model (linear model from earlier or logged model presented here) is a better fit for these data.
   

   
3. The output for the logged model is given below. Interpret the slope in context of the data.

   	Estimate	Std. Error	t value	Pr(\(\gt\)\(|\)t\(|\))
   (Intercept)	1.017	0.113	9.000	0.000
   hrs_work	0.058	0.003	21.086	0.000