15 Social experiment, Part I
A “social experiment” conducted by a TV program questioned what people do when they see a very obviously bruised woman getting picked on by her boyfriend. On two different occasions at the same restaurant, the same couple was depicted. In one scenario the woman was dressed “provocatively” and in the other scenario the woman was dressed “conservatively”. The table below shows how many restaurant diners were present under each scenario, and whether or not they intervened.
|
|
Scenario |
|
|
Provocative |
Conservative |
Total |
| Intervene |
Yes |
5 |
15 |
20 |
|
No |
15 |
10 |
25 |
|
Total |
20 |
25 |
45 |
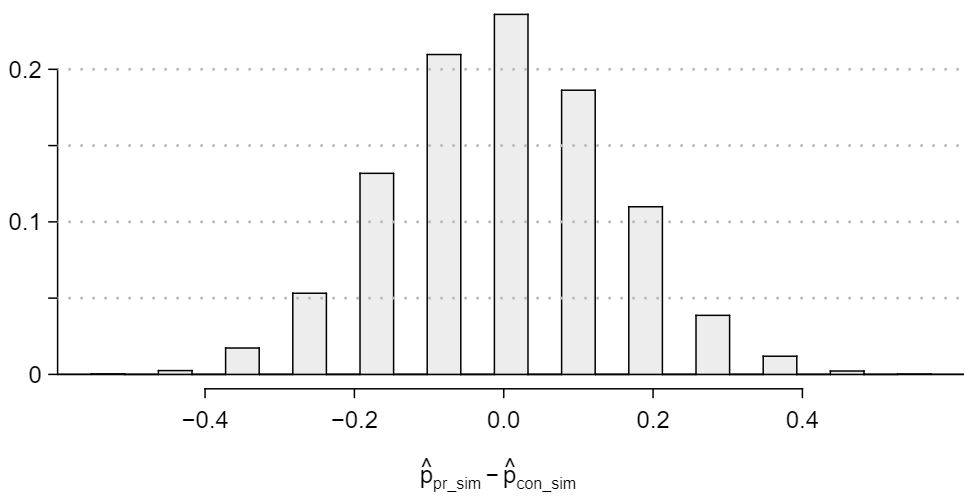
A simulation was conducted to test if people react differently under the two scenarios. 10,000 simulated differences were generated to construct the null distribution shown. The value \(\hat{p}_{pr, sim}\) represents the proportion of diners who intervened in the simulation for the provocatively dressed woman, and \(\hat{p}_{con, sim}\) is the proportion for the conservatively dressed woman.
- What are the hypotheses? For the purposes of this exercise, you may assume that each observed person at the restaurant behaved independently, though we would want to evaluate this assumption more rigorously if we were reporting these results. Answer
The subscript \(_{pr}\) corresponds to provocative and \(_{con}\) to conservative. (a) \(H_0: p_{pr} = p_{con}\text{.}\) \(H_A: p_{pr} \ne p_{con}\text{.}\)
- Calculate the observed difference between the rates of intervention under the provocative and conservative scenarios: \(\hat{p}_{pr} - \hat{p}_{con}\text{.}\) Answer
- Estimate the p-value using the figure above and determine the conclusion of the hypothesis test. Answer
The left tail for the p-value is calculated by adding up the two left bins: \(0.005+0.015=0.02\text{.}\) Doubling the one tail, the p-value is 0.04. (Students may have approximate results, and a small number of students may have a p-value of about 0.05.) Since the p-value is low, we reject \(H_0\text{.}\) The data provide strong evidence that people react differently under the two scenarios.
16 Is yawning contagious, Part I
An experiment conducted by the MythBusters, a science entertainment TV program on the Discovery Channel, tested if a person can be subconsciously influenced into yawning if another person near them yawns. 50 people were randomly assigned to two groups: 34 to a group where a person near them yawned (treatment) and 16 to a group where there wasn't a person yawning near them (control). The following table shows the results of this experiment. 6
|
|
Group |
|
|
Treatment |
Control |
Total |
| Result |
Yawn |
10 |
4 |
14 |
|
Not Yawn |
24 |
12 |
36 |
|
Total |
34 |
16 |
50 |
A simulation was conducted to understand the distribution of the test statistic under the assumption of independence: having someone yawn near another person has no influence on if the other person will yawn. In order to conduct the simulation, a researcher wrote yawn on 14 index cards and not yawn on 36 index cards to indicate whether or not a person yawned. Then he shuffled the cards and dealt them into two groups of size 34 and 16 for treatment and control, respectively. He counted how many participants in each simulated group yawned in an apparent response to a nearby yawning person, and calculated the difference between the simulated proportions of yawning as \(\hat{p}_{trtmt,sim} - \hat{p}_{ctrl,sim}\text{.}\) This simulation was repeated 10,000 times using software to obtain 10,000 differences that are due to chance alone. The histogram shows the distribution of the simulated differences.
What are the hypotheses?
Calculate the observed difference between the yawning rates under the two scenarios.
Estimate the p-value using the figure above and determine the conclusion of the hypothesis test.
17 Social experiment, Part II
In Exercise 5.5.15, we encountered a scenario where researchers were evaluating the impact of the way someone is dressed against the actions of people around them. In that exercise, researchers may have believed that dressing provocatively may reduce the chance of bystander intervention. One might be tempted to use a one-sided hypothesis test for this study. Discuss the drawbacks of doing so in 1-3 sentences.
AnswerThe primary concern is confirmation bias. If researchers look only for what they suspect to be true using a one-sided test, then they are formally excluding from consideration the possibility that the opposite result is true. Additionally, if other researchers believe the opposite possibility might be true, they would be very skeptical of the one-sided test.
18 Is yawning contagious, Part II
Exercise 5.5.16 describes an experiment by Myth Busters, where they examined whether a person yawning would affect whether others to yawn. The traditional belief is that yawning is contagious — one yawn can lead to another yawn, which might lead to another, and so on. In that exercise, there was the option of selecting a one-sided or two-sided test. Which would you recommend (or which did you choose)? Justify your answer in 1-3 sentences.
19 The Egyptian Revolution
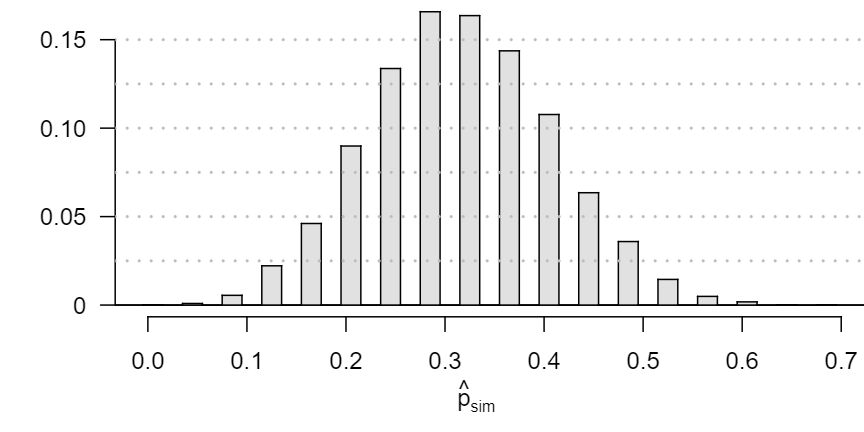
A popular uprising that started on January 25, 2011 in Egypt led to the 2011 Egyptian Revolution. Polls show that about 69% of American adults followed the news about the political crisis and demonstrations in Egypt closely during the first couple weeks following the start of the uprising. Among a random sample of 30 high school students, it was found that only 17 of them followed the news about Egypt closely during this time. 7
- Write the hypotheses for testing if the proportion of high school students who followed the news about Egypt is different than the proportion of American adults who did. Answer
\(H_0: p = 0.69\text{.}\) \(H_A: p \ne 0.69\text{.}\)
- Calculate the proportion of high schoolers in this sample who followed the news about Egypt closely during this time. Answer
\(\hat{p} = \frac{17}{30} = 0.57\text{.}\)
- Describe how to perform a simulation and, once you had results, how to estimate the p-value. Answer
The success-failure condition is not satisfied; note that it is appropriate to use the null value (\(p_0 = 0.69\)) to compute the expected number of successes and failures.
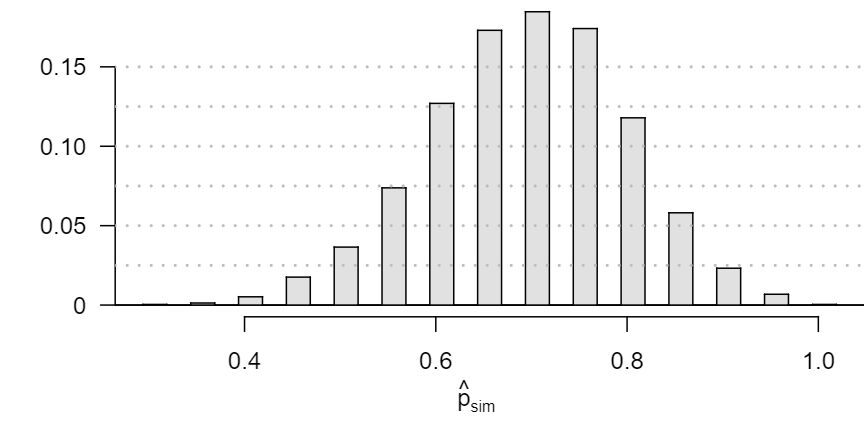
- Below is a histogram showing the distribution of \(\hat{p}_{sim}\) in 10,000 simulations under the null hypothesis. Estimate the p-value using the plot and determine the conclusion of the hypothesis test. Answer
Answers may vary. Each student can be represented with a card. Take 100 cards, 69 black cards representing those who follow the news about Egypt and 31 red cards representing those who do not. Shuffle the cards and draw with replacement (shuffling each time in between draws) 30 cards representing the 30 high school students. Calculate the proportion of black cards in this sample, \(\hat{p}_{sim}\text{,}\) i.e. the proportion of those who follow the news in the simulation. Repeat this many times (e.g. 10,000 times) and plot the resulting sample proportions. The p-value will be two times the proportion of simulations where \(\hat{p}_{sim} \le 0.57\text{.}\) (Note: we would generally use a computer to perform these simulations.)
The p-value is about \(0.001 + 0.005 + 0.020 + 0.035 + 0.075 = 0.136\text{,}\) meaning the two-sided p-value is about 0.272. Your p-value may vary slightly since it is based on a visual estimate. Since the p-value is greater than 0.05, we fail to reject \(H_0\text{.}\) The data do not provide strong evidence that the proportion of high school students who followed the news about Egypt is different than the proportion of American adults who did.
20 Assisted Reproduction
Assisted Reproductive Technology (ART) is a collection of techniques that help facilitate pregnancy (e.g. in vitro fertilization). A 2008 report by the Centers for Disease Control and Prevention estimated that ART has been successful in leading to a live birth in 31% of cases 8 . A new fertility clinic claims that their success rate is higher than average. A random sample of 30 of their patients yielded a success rate of 40%. A consumer watchdog group would like to determine if this provides strong evidence to support the company's claim.
Write the hypotheses to test if the success rate for ART at this clinic is significantly higher than the success rate reported by the CDC.
Describe a setup for a simulation that would be appropriate in this situation and how the p-value can be calculated using the simulation results.
Below is a histogram showing the distribution of \(\hat{p}_{sim}\) in 10,000 simulations under the null hypothesis. Estimate the p-value using the plot and use it to evaluate the hypotheses.
After performing this analysis, the consumer group releases the following news headline: “Infertility clinic falsely advertises better success rates”. Comment on the appropriateness of this statement.
21 Spam mail, Part I
The 2004 National Technology Readiness Survey sponsored by the Smith School of Business at the University of Maryland surveyed 418 randomly sampled Americans, asking them how many spam emails they receive per day. The survey was repeated on a new random sample of 499 Americans in 2009. 9
- What are the hypotheses for evaluating if the average spam emails per day has changed from 2004 to 2009. Answer
\(H_0\text{:}\) \(\mu_1 - \mu_2 = 0\text{,}\) i.e. there is no difference in the average number of spam emails each day for American between 2004 and 2009. \(H_A\text{:}\) \(\mu_1 - \mu_2 \neq 0\text{,}\) i.e. there is a difference between the average number of spam emails each day for Americans between 2004 and 2009.
- In 2004 the mean was 18.5 spam emails per day, and in 2009 this value was 14.9 emails per day. What is the point estimate for the difference between the two population means? Answer
\(18.5 - 14.9 = 3.6\) spam emails per day.
- A report on the survey states that the observed difference between the sample means is not statistically significant. Explain what this means in context of the hypothesis test and data. Answer
There is not convincing evidence that the observed difference is due to anything but chance. That is, observing a difference of 3.6 in the two sample means could reasonably be explained by chance alone.
- Would you expect a confidence interval for the difference between the two population means to contain 0? Explain your reasoning. Answer
Since the difference is not statistically significant, we would expect the confidence interval to contain 0.
22 Nearsightedness
It is believed that nearsightedness affects about 8% of all children. In a random sample of 194 children, 21 are nearsighted.
Construct hypotheses appropriate for the following question: do these data provide evidence that the 8% value is inaccurate?
What proportion of children in this sample are nearsighted?
Given that the standard error of the sample proportion is 0.0195 and the point estimate follows a nearly normal distribution, calculate the test statistic (the Z-statistic).
What is the p-value for this hypothesis test?
What is the conclusion of the hypothesis test?
23 Spam mail, Part II
The National Technology Readiness Survey from Exercise 5.5.21 also asked Americans how often they delete spam emails. 23% of the respondents in 2004 said they delete their spam mail once a month or less, and in 2009 this value was 16%.
- What are the hypotheses for evaluating if the proportion of those who delete their email once a month or less has changed from 2004 to 2009? Answer
\(H_0\text{:}\) \(p_1 - p_2 = 0\text{,}\) i.e. there is no difference in the fraction of Americans who say they delete their spam emails once a month or less.
\(H_A\text{:}\) \(p_1 - p_2 \neq 0\text{,}\) i.e. there is a difference in the fraction of Americans who say they delete their spam emails once a month or less.
- What is the point estimate for the difference between the two population proportions? Answer
\(0.23 - 0.16 = 0.07\text{.}\)
- A report on the survey states that the observed decrease from 2004 to 2009 is statistically significant. Explain what this means in context of the hypothesis test and the data. Answer
The difference of 0.07 (7%) is not easily explained by chance. That is, there is strong evidence that the fraction of Americans who say they delete their spam emails once a month or less has declined. (Notice that we can assert the direction, even in this two-sided test.)
- Would you expect a confidence interval for the difference between the two population proportions to contain 0? Explain your reasoning. Answer
Because the difference is statistically significant, 0 is not a plausible value for the difference, meaning we would not expect the confidence interval to contain 0.
24 Unemployment and relationship problems
A USA Today/Gallup poll conducted between 2010 and 2011 asked a group of unemployed and underemployed Americans if they have had major problems in their relationships with their spouse or another close family member as a result of not having a job (if unemployed) or not having a full-time job (if underemployed). 27% of the 1,145 unemployed respondents and 25% of the 675 underemployed respondents said they had major problems in relationships as a result of their employment status.
What are the hypotheses for evaluating if the proportions of unemployed and underemployed people who had relationship problems were different?
The p-value for this hypothesis test is approximately 0.35. Explain what this means in context of the hypothesis test and the data.
25 Testing for Fibromyalgia
A patient named Diana was diagnosed with Fibromyalgia, a long-term syndrome of body pain, and was prescribed anti-depressants. Being the skeptic that she is, Diana didn't initially believe that anti-depressants would help her symptoms. However after a couple months of being on the medication she decides that the anti-depressants are working, because she feels like her symptoms are in fact getting better.
- Write the hypotheses in words for Diana's skeptical position when she started taking the anti-depressants. Answer
\(H_0\text{:}\) Anti-depressants do not help symptoms of Fibromyalgia. \(H_A\text{:}\) Anti-depressants do treat symptoms of Fibromyalgia. Remark: Diana might also have taken special note if her symptoms got much worse, so a more scientific approach would have been to use a two-sided test. While parts (b) and (c) use the one-sided version, your answers will be a little different if you used a two-sided test.
- What is a Type 1 Error in this context? Answer
Concluding that anti-depressants work for the treatment of Fibromyalgia symptoms when they actually do not.
- What is a Type 2 Error in this context? Answer
Concluding that anti-depressants do not work for the treatment of Fibromyalgia symptoms when they actually do.
26 Testing for food safety
A food safety inspector is called upon to investigate a restaurant with a few customer reports of poor sanitation practices. The food safety inspector uses a hypothesis testing framework to evaluate whether regulations are not being met. If he decides the restaurant is in gross violation, its license to serve food will be revoked.
Write the hypotheses in words.
What is a Type 1 Error in this context?
What is a Type 2 Error in this context?
Which error is more problematic for the restaurant owner? Why?
Which error is more problematic for the diners? Why?
As a diner, would you prefer that the food safety inspector requires strong evidence or very strong evidence of health concerns before revoking a restaurant's license? Explain your reasoning.
27 True / False
Determine whether the following statement is true or false, and explain your reasoning: “A cutoff of \(\alpha\) = 0.05 is the ideal value for all hypothesis tests.”
AnswerFalse. It is appropriate to adjust the significance level to reflect the consequences of a Type 1 or Type 2 Error, and it is also be appropriate to consider additional context of the application.
28 True / False
Determine whether the following statement is true or false, and explain your reasoning: “Power of a test and the probability of making a Type 1 Error are complements.”
29 Which is higher?
In each part below, there is a value of interest and two scenarios (I and II). For each part, report if the value of interest is larger under scenario I, scenario II, or whether the value is equal under the scenarios.
- The standard error of \(\bar{x}\) when \(s = 120\) and (I) n = 25 or (II) n = 125. Answer
Scenario I is higher. Recall that a sample mean based on less data tends to be less accurate and have larger standard errors.
- The margin of error of a confidence interval when the confidence level is (I) 90% or (II) 80%. Answer
Scenario I is higher. The higher the confidence level, the higher the corresponding margin of error.
- The p-value for a Z-statistic of 2.5 when (I) n = 500 or (II) n = 1000. Answer
They are equal. The sample size does not affect the calculation of the p-value for a given Z-score.
- The probability of making a Type 2 Error when the alternative hypothesis is true and the significance level is (I) 0.05 or (II) 0.10. Answer
Scenario I is higher. If the null hypothesis is harder to reject (lower \(\alpha\)), then we are more likely to make a Type 2 error when the alternative hypothesis is true.
30 True or false
Determine if the following statements are true or false, and explain your reasoning. If false, state how it could be corrected.
If a given value (for example, the null hypothesized value of a parameter) is within a 95% confidence interval, it will also be within a 99% confidence interval.
Decreasing the significance level (\(\alpha\)) will increase the probability of making a Type 1 Error.
Suppose the null hypothesis is \(\mu = 5\) and we fail to reject \(H_0\text{.}\) Under this scenario, the true population mean is 5.
If the alternative hypothesis is true, then the probability of making a Type 2 Error and the power of a test add up to 1.
With large sample sizes, even small differences between the null value and the true value of the parameter, a difference often called the effect size, will be identified as statistically significant.