Skip to main content

Section 3.2 Conditional probability

Probability Trees video
Figure 3.2.1 Probability Trees video

The family_college data set contains a sample of 792 cases with two variables, teen and parents, and is summarized in Table 3.2.2. 1 A simulated data set based on real population summaries at nces.ed.gov/pubs2001/2001126.pdf The teen variable is either college or not, where the teenager is labeled as college if she went to college immediately after high school. The parents variable takes the value degree if at least one parent of the teenager completed a college degree.

parents
degree not Total
teen college 231 214 445
not 49 298 347
Total 280 512 792
Table 3.2.2 Contingency table summarizing the family_college data set.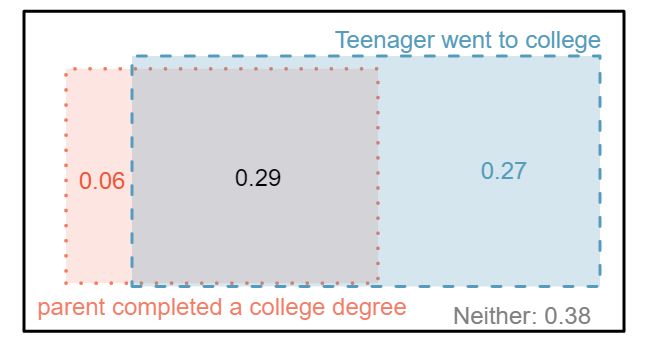
Figure 3.2.3 A Venn diagram using boxes for the family_college data set.

If at least one parent completed a college degree, what is the chance their teenager attended college right after high school? 2 We can estimate this probability using the data. Of the 280 cases in this data set where parents takes value degree, 231 represent cases where the teen variable takes value college:

\begin{gather*} P(\text{teen college given parents degree}) = \frac{231}{280} = 0.825 \end{gather*}

A teenager is randomly selected from the sample and she did not attend college right after high school. What is the probability that at least one of her parents has a college degree? 3 If the teenager did not attend, then she is one of the 347 teens in the second row. Of these 347 teens, 49 had at least one parent who got a college degree:

\begin{gather*} P(\text{parents degree given teen not}) = \frac{49}{347} = 0.141 \end{gather*}

Subsection 3.2.1 Marginal and joint probabilities

Table 3.2.2 includes row and column totals for each variable separately in the family_college data set. These totals represent marginal probabilities for the sample, which are the probabilities based on a single variable without conditioning on any other variables. For instance, a probability based solely on the teen variable is a marginal probability:

\begin{gather*} P(\text{ teen college}) = \frac{445}{792} = 0.56 \end{gather*}

A probability of outcomes for two or more variables or processes is called a joint probability:

\begin{gather*} P(\text{ teen college and parents not }) = \frac{214}{792} = 0.27 \end{gather*}

It is common to substitute a comma for “and” in a joint probability, although either is acceptable. That is,

\begin{gather*} P(\text{teen college, parents not})\\ \text{means the same thing as}\\ P(\text{teen college and parents not}) \end{gather*}
Marginal and joint probabilities

If a probability is based on a single variable, it is a marginal probability. The probability of outcomes for two or more variables or processes is called a joint probability.

We use table proportions to summarize joint probabilities for the family_college sample. These proportions are computed by dividing each count in Table 3.2.2 by the table's total, 792, to obtain the proportions in Table 3.2.6. The joint probability distribution of the parents and teen variables is shown in Table 3.2.7.

parents: degree parents: not Total
teen: college 0.29 0.27 0.56
teen: not 0.06 0.38 0.44
Total 0.35 0.65 1.00
Table 3.2.6 Probability table summarizing whether at least one parent had a college degree and the teenager attended college.
Joint outcome Probability
parents degree and teen college 0.29
parents degree and teen not 0.06
parents not and teen college 0.27
parents not and teen not 0.38
Total 1.00
Table 3.2.7 Joint probability distribution for the family_college data set.

Verify Table 3.2.7 represents a probability distribution: events are disjoint, all probabilities are non-negative, and the probabilities sum to 1. 4 Each of the four outcome combination are disjoint, all probabilities are indeed non-negative, and the sum of the probabilities is \(0.29 + 0.06 + 0.27 + 0.38 = 1.00\text{.}\)

We can compute marginal probabilities using joint probabilities in simple cases. For example, the probability a random teenager from the study went to college is found by summing the outcomes from Table 3.2.7 where teen takes value college:

\begin{gather*} P(\text{teen college}) = P(\text{parents degree and teen college})\\ + P(\text{parents not and teen college})\\ = 0.29 + 0.27\\ = 0.56 \end{gather*}

Subsection 3.2.2 Defining conditional probability

There is some connection between education level of parents and of the teenager: a college degree by a parent is associated with college attendance of the teenager. In this section, we discuss how to use information about associations between two variables to improve probability estimation.

The probability that a random teenager from the study attended college is 0.56. Could we update this probability if we knew that one of the teen's parents has a college degree? Absolutely. To do so, we limit our view to only those 280 cases where a parent has a college degree and look at the fraction where the teenager attended college:

\begin{gather*} P(\text{teen college given parents degree} ) = \frac{231}{280} = 0.825 \end{gather*}

We call this a conditional probability because we computed the probability under a condition: a parent has a college degree. There are two parts to a conditional probability, the outcome of interest and the condition. It is useful to think of the condition as information we know to be true, and this information usually can be described as a known outcome or event.

We separate the text inside our probability notation into the outcome of interest and the condition:

\begin{gather*} P(\text{teen college given parents degree} )\\ = P(\text{teen college} | \text{parents degree}) = \frac{231}{280} = 0.825 \end{gather*}

The vertical bar “\(|\)” is read as given 5 \(P(A | B)\) is the Probability of outcome \(A\) given \(B\).

In (), we computed the probability a teen attended college based on the condition that at least one parent has a college degree as a fraction:

\begin{align*} \amp \amp P(\text{college} | \text{parents degree} )\\ \amp \amp = \frac{\text{# cases where teen college and parents degree}}{\text{# cases where parents degree}} \\ \amp \amp = \frac{231}{280} = 0.825 \end{align*}

We considered only those cases that met the condition, parents degree, and then we computed the ratio of those cases that satisfied our outcome of interest, the teenager attended college.

Frequently, marginal and joint probabilities are provided instead of count data. For example, disease rates are commonly listed in percentages rather than in a count format. We would like to be able to compute conditional probabilities even when no counts are available, and we use Equation () as a template to understand this technique.

We considered only those cases that satisfied the condition, parents degree. Of these cases, the conditional probability was the fraction who represented the outcome of interest, teen college. Suppose we were provided only the information in Table 3.2.6, i.e. only probability data. Then if we took a sample of 1000 people, we would anticipate about 35% or \(0.35\times 1000 = 350\) would meet the information criterion (parents degree). Similarly, we would expect about 29% or \(0.29\times 1000 = 290\) to meet both the information criteria and represent our outcome of interest. Thus, the conditional probability could be computed:

\begin{align} \amp P(\text{teen college} \ |\ \text{parents degree} )\tag{3.2.1}\\ \amp = \frac{\text{# (teen college and parents degree)}}{\text{# (parents degree)}}\tag{3.2.2}\\ \amp = \frac{290}{350} = \frac{0.29}{0.35} = 0.829\text{ (different from 0.825 due to rounding error) }\label{stUserPUsedHypSampSize}\tag{3.2.3} \end{align}

In Equation (3.2.3), we examine exactly the fraction of two probabilities, 0.29 and 0.35, which we can write as

\begin{gather*} P(\text{teen college and parents degree} ) \text{ and } P(\text{parents degree} ). \end{gather*}

The fraction of these probabilities is an example of the general formula for conditional probability.

Conditional probability

The conditional probability of the outcome of interest \(A\) given condition \(B\) is computed as the following:

\begin{gather} P(A | B) = \frac{P(A\text{ and } B)}{P(B)}\label{condProbEq}\tag{3.2.4} \end{gather}

  1. Write out the following statement in conditional probability notation: “The probability a random case where neither parent has a college degree if it is known that the teenager didn't attend college right after high school”. Notice that the condition is now based on the teenager, not the parent. 6 \(P(\text{parents not} \ |\ \text{teen not} )\text{.}\)

  2. Determine the probability from part (a). Table 3.2.6 may be helpful. 7 Equation (3.2.4) for conditional probability indicates we should first find \(P(\text{parents not and teen not} ) = 0.38\) and \(P(\text{teen not} ) = 0.44\text{.}\) Then the ratio represents the conditional probability: \(0.38 / 0.44 = 0.864\text{.}\)

  1. Determine the probability that one of the parents has a college degree if it is known the teenager did not attend college. 8 This probability is \(\frac{P(\text{parents degree, teen not} )}{P(\text{teen not} )} = \frac{0.06}{0.44} = 0.136\text{.}\)

  2. Using the answers from part (a) and Example 3.2.9(b), compute

    \begin{align*} \amp P(\text{parents degree} \ |\ \text{teen not} )\\ \amp + P(\text{parents not} \ |\ \text{teen not} ) \end{align*}

     9 The total equals 1.

  3. Provide an intuitive argument to explain why the sum in (b) is1. 10 Under the condition the teenager didn't attend college, the parents must either have a college degree or not. The complement still works, provided the probabilities condition on the same information.

The data indicate there is an association between parents having a college degree and their teenager attending college. Does this mean the parents' college degree(s) caused the teenager to go to college? 11 No. While there is an association, the data are observational. Two potential confounding variables include income and region. Can you think of others?

Subsection 3.2.3 Smallpox in Boston, 1721

The smallpox data set provides a sample of 6,224 individuals from the year 1721 who were exposed to smallpox in Boston. 12 Fenner F. 1988. Smallpox and Its Eradication (History of International Public Health, No. 6). Geneva: World Health Organization. ISBN 92-4-156110-6. Doctors at the time believed that inoculation, which involves exposing a person to the disease in a controlled form, could reduce the likelihood of death.

Each case represents one person with two variables: inoculated and result. The variable inoculated takes two levels: yes or no, indicating whether the person was inoculated or not. The variable result has outcomes lived or died. These data are summarized in Table 3.2.12 and Table 3.2.13.

inoculated
yes no Total
result lived 238 5136 5374
died 6 844 850
Total 244 5980 6224
Table 3.2.12 Contingency table for the smallpox data set.
inoculated
yes no Total
result lived 0.0382 0.8252 0.8634
died 0.0010 0.1356 0.1366
Total 0.0392 0.9608 1.0000
Table 3.2.13 Table proportions for the smallpox data, computed by dividing each count by the table total, 6224.

Write out, in formal notation, the probability a randomly selected person who was not inoculated died from smallpox, and find this probability.  13 \(P(\)result = died \(|\) not inoculated\() = \frac{P(\text{result} = \text{died and not inoculated} )}{P(\text{not inoculated} )} = \frac{0.1356}{0.9608} = 0.1411\text{.}\)

Determine the probability that an inoculated person died from smallpox. How does this result compare with the result of Example 3.2.14? 14 \(P(\)died \(|\) inoculated\() = \frac{P(\text{died and inoculated} )}{P(\text{inoculated} )} = \frac{0.0010}{0.0392} = 0.0255\text{.}\) The death rate for individuals who were inoculated is only about 1 in 40 while the death rate is about 1 in 7 for those who were not inoculated.

The people of Boston self-selected whether or not to be inoculated.

  1. Is this study observational or was this an experiment? 15 Observational.

  2. Can we infer any causal connection using these data? 16 No, we cannot infer causation from this observational study.

  3. What are some potential confounding variables that might influence whether someone lived or died and also affect whether that person was inoculated? 17 Accessibility to the latest and best medical care, so income may play a role. There are other valid answers for part (3)

Subsection 3.2.4 General multiplication rule

Subsection 3.1.5 introduced the Multiplication Rule for independent processes. Here we provide the General Multiplication Rule for events that might not be independent.

General Multiplication Rule

If \(A\) and \(B\) represent two outcomes or events, then

\begin{gather*} P(A\text{ and } B) = P(A | B)\times P(B) \end{gather*}

For the term \(P(A | B)\text{,}\) it is useful to think of \(A\) as the outcome of interest and \(B\) as the condition.

This General Multiplication Rule is simply a rearrangement of the definition for conditional probability in Equation (3.2.4).

Consider the smallpox data set. Suppose we are given only two pieces of information: 96.08% of residents were not inoculated, and 85.88% of the residents who were not inoculated ended up surviving. How could we compute the probability that a resident was not inoculated and lived?

Solution

We will compute our answer using the General Multiplication Rule and then verify it using Table 3.2.13. We want to determine

\begin{gather*} P(\text{lived and not inoculated} ) \end{gather*}

and we are given that

\begin{gather*} P(\text{lived} \ |\ \text{not inoculated} )=0.8588\\ P(\text{not inoculated} )=0.9608 \end{gather*}

Among the 96.08% of people who were not inoculated, 85.88% survived:

\begin{gather*} P(\text{lived and not inoculated} ) = 0.8588\times 0.9608 = 0.8251 \end{gather*}

This is equivalent to the General Multiplication Rule. We can confirm this probability in Table 3.2.13 at the intersection of no and lived (with a small rounding error).

Use \(P(\)inoculated\() = 0.0392\) and \(P(\)lived \(|\) inoculated\() = 0.9754\) to determine the probability that a person was both inoculated and lived. 18 The answer is 0.0382, which can be verified using Table 3.2.13.

If 97.54% of the people who were inoculated lived, what proportion of inoculated people must have died? 19 There were only two possible outcomes: lived or died. This means that 100% - 97.45% = 2.55% of the people who were inoculated died.

Based on the probabilities computed above, does it appear that inoculation is effective at reducing the risk of death from smallpox? 20 The samples are large relative to the difference in death rates for the “inoculated” and “not inoculated” groups, so it seems there is an association between inoculated and outcome. However, as noted in the solution to Example 3.2.16, this is an observational study and we cannot be sure if there is a causal connection. (Further research has shown that inoculation is effective at reducing death rates.)

Subsection 3.2.5 Sampling from a small population

Professors sometimes select a student at random to answer a question. If each student has an equal chance of being selected and there are 15 people in your class, what is the chance that she will pick you for the next question?

Solution

If there are 15 people to ask and none are skipping class, then the probability is \(1/15\text{,}\) or about \(0.067\text{.}\)

If the professor asks 3 questions, what is the probability that you will not be selected? Assume that she will not pick the same person twice in a given lecture.

Solution

For the first question, she will pick someone else with probability \(14/15\text{.}\) When she asks the second question, she only has 14 people who have not yet been asked. Thus, if you were not picked on the first question, the probability you are again not picked is \(13/14\text{.}\) Similarly, the probability you are again not picked on the third question is \(12/13\text{,}\) and the probability of not being picked for any of the three questions is

\begin{align*} \amp \amp P(\text{ not picked in 3 questions } )\\ \amp \amp = P(\text{Q1} = \text{not_picked}, \text{Q2} = \text{not_picked}, \text{Q3} = \text{not_picked}.)\\ \amp \amp = \frac{14}{15}\times\frac{13}{14}\times\frac{12}{13} = \frac{12}{15} = 0.80 \end{align*}

What rule permitted us to multiply the probabilities in Guided Practice 3.2.22? 21 The three probabilities we computed were actually one marginal probability, \(P(\)Q1\(=\)not_picked\()\text{,}\) and two conditional probabilities:

\begin{align*} \amp P(\text{Q2} = \text{not_picked} \ |\ \text{Q1} = \text{not_picked} )\\ \amp P(\text{Q3} = \text{not_picked} \ |\ \text{Q1} = \text{not_picked}, \text{Q2} = \text{not_picked} ) \end{align*}
Using the General Multiplication Rule, the product of these three probabilities is the probability of not being picked in 3 questions.

Suppose the professor randomly picks without regard to who she already selected, i.e. students can be picked more than once. What is the probability that you will not be picked for any of the three questions?

Solution

Each pick is independent, and the probability of not being picked for any individual question is \(14/15\text{.}\) Thus, we can use the Multiplication Rule for independent processes.

\begin{align*} \amp \amp P(\text{ not picked in 3 questions } )\\ \amp \amp = P(\text{Q1} = \text{not_picked}, \text{Q2} = \text{not_picked}, \text{Q3} = \text{not_picked}.)\\ \amp \amp = \frac{14}{15}\times\frac{14}{15}\times\frac{14}{15} = 0.813 \end{align*}

You have a slightly higher chance of not being picked compared to when she picked a new person for each question. However, you now may be picked more than once.

Under the setup of Guided Practice 3.2.24, what is the probability of being picked to answer all three questions? 22 \(P(\)being picked to answer all three questions\() = \left(\frac{1}{15}\right)^3 = 0.00030\text{.}\)

If we sample from a small population without replacement, we no longer have independence between our observations. In Guided Practice 3.2.22, the probability of not being picked for the second question was conditioned on the event that you were not picked for the first question. In Guided Practice 3.2.24, the professor sampled her students with replacement: she repeatedly sampled the entire class without regard to who she already picked.

Your department is holding a raffle. They sell 30 tickets and offer seven prizes.

  1. They place the tickets in a hat and draw one for each prize. The tickets are sampled without replacement, i.e. the selected tickets are not placed back in the hat. What is the probability of winning a prize if you buy one ticket? 23 First determine the probability of not winning. The tickets are sampled without replacement, which means the probability you do not win on the first draw is \(29/30\text{,}\) \(28/29\) for the second, ..., and \(23/24\) for the seventh. The probability you win no prize is the product of these separate probabilities: \(23/30\text{.}\) That is, the probability of winning a prize is \(1 - 23/30 = 7/30 = 0.233\text{.}\)

  2. What if the tickets are sampled with replacement? 24 When the tickets are sampled with replacement, there are seven independent draws. Again we first find the probability of not winning a prize: \((29/30)^7 = 0.789\text{.}\) Thus, the probability of winning (at least) one prize when drawing with replacement is 0.211.

Compare your answers in Example 3.2.26. How much influence does the sampling method have on your chances of winning a prize? 25 There is about a 10% larger chance of winning a prize when using sampling without replacement. However, at most one prize may be won under this sampling procedure.

Had we repeated Example 3.2.26 with 300 tickets instead of 30, we would have found something interesting: the results would be nearly identical. The probability would be 0.0233 without replacement and 0.0231 with replacement. When the sample size is only a small fraction of the population (under 10%), observations are nearly independent even when sampling without replacement.

Subsection 3.2.6 Independence considerations in conditional probability

If two processes are independent, then knowing the outcome of one should provide no information about the other. We can show this is mathematically true using conditional probabilities.

Let \(X\) and \(Y\) represent the outcomes of rolling two dice. (a) What is the probability that the first die, \(X\text{,}\) is 1? (b) What is the probability that both \(X\) and \(Y\) are 1? (c) Use the formula for conditional probability to compute \(P(Y =\) 1 \(| X =\) 1\()\text{.}\) (d) What is \(P(Y=1)\text{?}\) Is this different from the answer from part (c)? Explain. 26 Brief solutions: (a) \(1/6\text{.}\) (b) \(1/36\text{.}\) (c) \(\frac{P(Y = 1 \text { and } X=1)}{P(X=1)} = \frac{1/36}{1/6} = 1/6\text{.}\) (d) The probability is the same as in part (c): \(P(Y=1)=1/6\text{.}\) The probability that \(Y=1\) was unchanged by knowledge about \(X\text{,}\) which makes sense as \(X\) and \(Y\) are independent.

We can show in Example 3.2.28(c) that the conditioning information has no influence by using the Multiplication Rule for independence processes:

\begin{align*} P(Y=1 | X=1) \amp =\amp \frac{P(Y=1 \text{ and } X=1)}{P(X=1)}\\ \amp =\amp \frac{P(Y=1)\times \color{oiGB}P(X=1)}{\color{oiGB}P(X=1)}\\ \amp =\amp P(Y=1 ) \end{align*}

Ron is watching a roulette table in a casino and notices that the last five outcomes were black. He figures that the chances of getting black six times in a row is very small (about \(1/64\)) and puts his paycheck on red. What is wrong with his reasoning? 27 He has forgotten that the next roulette spin is independent of the previous spins. Casinos do employ this practice; they post the last several outcomes of many betting games to trick unsuspecting gamblers into believing the odds are in their favor. This is called the gambler's fallacy.

Subsection 3.2.7 Checking for independent and mutually exclusive events

If \(A\) and \(B\) are independent events, then the probability of \(A\) being true is unchanged if \(B\) is true. Mathematically, this is written as

\begin{align*} P(A|B) \amp = P(A) \end{align*}

The General Multiplication Rule states that \(P(A\text{ and } B)\) equals \(P(A | B)\times P(B)\text{.}\) If \(A\) and \(B\) are independent events, we can replace \(P(A|B)\) with \(P(A)\) and the following multiplication rule applies:

\begin{align*} P(A\text{ and } B) \amp = P(A)\times P(B) \end{align*}
TIP:Checking whether two events are independent

When checking whether two events \(A\) and \(B\) are independent, verify one of the following equations holds (there is no need to check both equations):

\begin{align*} P(A|B) \amp = P(A)\amp P(A\text{ and } B) \amp = P(A)\times P(B) \end{align*}

If the equation that is checked holds true (the left and right sides are equal), \(A\) and \(B\) are independent. If the equation does not hold, then \(A\) and \(B\) are dependent.

Are teenager college attendance and parent college degrees independent or dependent? Table 3.2.31 may be helpful.

Solution

We'll use the first equation above to check for independence. If the teen and parents variables are independent, it must be true that

\begin{align*} P(\text{teen college} \|\ \text{parent degree} ) \amp = P(\text{teen college} ) \end{align*}

Using Table 3.2.31, we check whether equality holds in this equation.

\begin{align*} P(\text{teen college} \ |\ \text{parent degree} ) \amp \overset{?}{=} P(\text{teen college} )\\ 0.83 \amp \neq 0.56 \end{align*}

The value 0.83 came from a probability calculation using Table 3.2.31: \(\frac{231}{280} \approx 0.83\text{.}\) Because the sides are not equal, teenager college attendance and parent degree are dependent. That is, we estimate the probability a teenager attended college to be higher if we know that one of the teen's parents has a college degree.

parents
degree not Total
teen college 231 214 445
not 49 298 347
Total 280 512 792
Table 3.2.31 Contingency table summarizing the family_college data set.

Use the second equation in the box above to show that teenager college attendance and parent college degrees are dependent. 28 We check for equality in the following equation:

\begin{align*} P(\text{teen college, parent degree} )\amp \overset{?}{=} P(\text{teen college} )\times P(\text{parent degree} )\\ \frac{231}{792}=0.292 \amp \neq \frac{445}{792}\times \frac{280}{792}=0.199 \end{align*}
These terms are not equal, which confirms what we learned in Guided Practice 3.2.30: teenager college attendance and parent college degrees are dependent.

If \(A\) and \(B\) are mutually exclusive events, then \(A\) and \(B\) cannot occur at the same time. Mathematically, this is written as

\begin{align*} P(A \text{ and } B) \amp = 0 \end{align*}

The General Addition Rule states that \(P(A\text{ or } B) \text{ equals } P(A) + P(B) - P(A\text{ and } B)\text{.}\) If \(A\) and \(B\) are mutually exclusive events, we can replace \(P(A \text{ and } B)\) with 0 and the following addition rule applies:

\begin{align*} P(A\text{ or } B) \amp = P(A) + P(B) \end{align*}
TIP: Checking whether two events are mutually exclusive (disjoint)

If \(A\) and \(B\) are mutually exclusive events, then they cannot occur at the same time. If asked to determine if events \(A\) and \(B\) are mutually exclusive, verify one of the following equations holds (there is no need to check both equations):

\begin{align*} P(A \text{ and } B) \amp = 0\amp P(A\text{ or } B) \amp = P(A) + P(B) \end{align*}

If the equation that is checked holds true (the left and right sides are equal), \(A\) and \(B\) are mutually exclusive. If the equation does not hold, then \(A\) and \(B\) are not mutually exclusive.

Are teen college attendance and parent college degrees mutually exclusive?

Solution

Looking in the table, we see that there are 231 instances where both the teenager attended college and parents have a degree, indicating the probability of both events occurring is greater than 0. Since we have found an example where both of these events happen together, these two events are not mutually exclusive. We could more formally show this by computing the probability both events occur at the same time:

\begin{gather*} P(\text{teen college, parent degree} ) = \frac{231}{792}\neq 0 \end{gather*}

Since this probability is not zero, teenager college attendance and parent college degrees are not mutually exclusive.

TIP: Mutually exclusive and independent are different

If two events are mutually exclusive, then if one is true, the other cannot be true. This implies the two events are in some way connected, meaning they must be dependent.

If two events are independent, then if one occurs, it is still possible for the other to occur, meaning the events are not mutually exclusive.

Caution: Dependent events need not be mutually exclusive.

If two events are dependent, we cannot simply conclude they are mutually exclusive. For example, the college attendance of teenagers and a college degree by one of their parents are dependent, but those events are not mutually exclusive.

Subsection 3.2.8 Tree diagrams

Tree diagrams are a tool to organize outcomes and probabilities around the structure of the data. They are most useful when two or more processes occur in a sequence and each process is conditioned on its predecessors.

The smallpox data fit this description. We see the population as split by inoculation: yes and no. Following this split, survival rates were observed for each group. This structure is reflected in the tree diagram shown in Figure 3.2.34. The first branch for inoculation is said to be the primary branch while the other branches are secondary.

Figure 3.2.34 A tree diagram of the smallpox data set.

Tree diagrams are annotated with marginal and conditional probabilities, as shown in Figure 3.2.34. This tree diagram splits the smallpox data by inoculation into the yes and no groups with respective marginal probabilities 0.0392 and 0.9608. The secondary branches are conditioned on the first, so we assign conditional probabilities to these branches. For example, the top branch in Figure 3.2.34 is the probability that lived conditioned on the information that inoculated. We may (and usually do) construct joint probabilities at the end of each branch in our tree by multiplying the numbers we come across as we move from left to right. These joint probabilities are computed using the General Multiplication Rule:

\begin{align*} P(\text{inoculated and lived} ) \amp = P(\text{inoculated} )\times P(\text{lived} \ |\ \text{inoculated} )\\ \amp = 0.0392\times 0.9754\\ \amp =0.0382 \end{align*}

What is the probability that a randomly selected person who was inoculated died?

Solution

This is equivalent to \(P(\text{died} \ |\ \text{inoculated} )\text{.}\) This conditional probability can be found in the second branch as 0.0246.

What is the probability that a randomly selected person lived?

Solution

There are two ways that a person could have lived: be inoculated and live OR not be inoculated and live. To find this probability, we sum the two disjoint probabilities:

\begin{gather*} P(\text{lived} ) = 0.0392 \times 0.9745 + 0.9608 \times 0.8589 = 0.03824 + 0.82523 = 0.86347 \end{gather*}

After an introductory statistics course, 78% of students can successfully construct tree diagrams. Of those who can construct tree diagrams, 97% passed, while only 57% of those students who could not construct tree diagrams passed.

  1. Organize this information into a tree diagram.

  2. What is the probability that a student who was able to construct tree diagrams did not pass?

  3. What is the probability that a randomly selected student was able to successfully construct tree diagrams and passed?

  4. What is the probability that a randomly selected student passed?

 29 a. The tree diagram is shown below.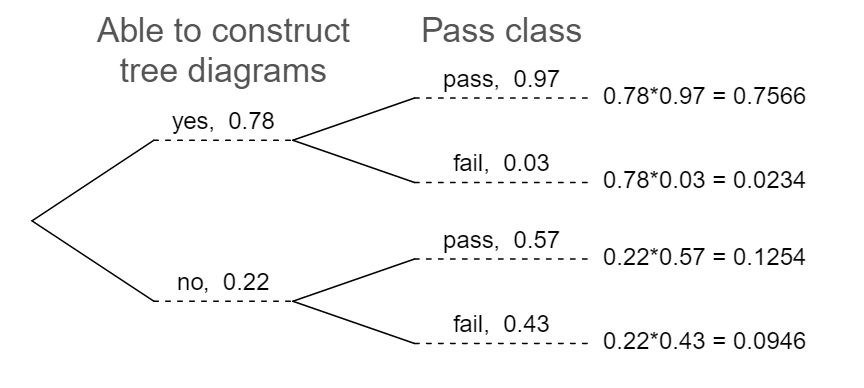

b. \(P(\)not pass \(|\) able to construct tree diagram\() = 0.03\text{.}\) c. \(P(\)able to construct tree diagrams and passed\() = P(\)able to construct tree diagrams\() \times P(\)passed \(|\) able to construct tree diagrams\() = 0.78 \times 0.97 = 0.7566\text{.}\) d. \(P(\)passed\() = 0.7566 + 0.1254 = 0.8820\text{.}\)

Subsection 3.2.9 Bayes' Theorem

In many instances, we are given a conditional probability of the form

\begin{gather*} P(\text{ statement about variable 1 } \ |\ \text{ statement about variable 2 } ) \end{gather*}

but we would really like to know the inverted conditional probability:

\begin{gather*} P(\text{ statement about variable 2 } \ |\ \text{ statement about variable 1 } ) \end{gather*}

For example, instead of wanting to know \(P(\)lived \(|\) inoculated\()\text{,}\) we might want to know \(P(\)inoculated \(|\) lived\()\text{.}\) This is more challenging because it cannot be read directly from the tree diagram. In these instances we use Bayes' Theorem. Let's begin by looking at a new example.

In Canada, about 0.35% of women over 40 will develop breast cancer in any given year. A common screening test for cancer is the mammogram, but this test is not perfect. In about 11% of patients with breast cancer, the test gives a false negative: it indicates a woman does not have breast cancer when she does have breast cancer. Similarly, the test gives a false positive in 7% of patients who do not have breast cancer: it indicates these patients have breast cancer when they actually do not. 30 The probabilities reported here were obtained using studies reported at http://www.breastcancer.org and https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1173421/. If we tested a random woman over 40 for breast cancer using a mammogram and the test came back positive — that is, the test suggested the patient has cancer — what is the probability that the patient actually has breast cancer?

Solution

We are given sufficient information to quickly compute the probability of testing positive if a woman has breast cancer (\(1.00 - 0.11 = 0.89\)). However, we seek the inverted probability of cancer given a positive test result:

\begin{gather*} P(\text{ has BC } \ |\ \text{ mammogram\(^+\) } ) \end{gather*}

Here, “has BC” is an abbreviation for the patient actually having breast cancer, and “mammogram\(^+\)” means the mammogram screening was positive, which in this case means the test suggests the patient has breast cancer. (Watch out for the non-intuitive medical language: a positive test result suggests the possible presence of cancer in a mammogram screening.) We can use the conditional probability formula from the previous section: \(P(A|B) = \frac{P(A \text{ and } B)}{P(B)}\text{.}\) Our conditional probability can be found as follows:

\begin{align*} P(\text{ has BC \(|\) mammogram\(^+\) } ) \amp = \frac{P(\text{ has BC and mammogram\(^+\) } )}{P(\text{ mammogram\(^+\) } )} \end{align*}

The probability that a mammogram is positive is as follows.

\begin{gather*} P(\text{ mammogram\(^+\) } )=P(\text{ has BC and mammogram\(^+\) } ) + P(\text{ no BC and mammogram\(^+\) } ) \end{gather*}

A tree diagram is useful for identifying each probability and is shown in Figure 3.2.39. Using the tree diagram, we find that

\begin{align*} P(\amp \text{ has BC \(|\) mammogram\(^+\) } )\\ \amp = \frac{P(\text{ has BC and mammogram\(^+\) } )}{P(\text{ has BC and mammogram\(^+\) } ) + P(\text{ no BC and mammogram\(^+\) } )}\\ \amp = \frac{0.0035(0.89)}{0.0035(0.89)+0.9965(0.07)}\\ \amp = \frac{0.00312}{0.07288}\approx 0.0428 \end{align*}

That is, even if a patient has a positive mammogram screening, there is still only a 4% chance that she has breast cancer.

Figure 3.2.39 Tree diagram for Guided Practice 3.2.38, computing the probability a random patient who tests positive on a mammogram actually has breast cancer.

Guided Practice 3.2.38 highlights why doctors often run more tests regardless of a first positive test result. When a medical condition is rare, a single positive test isn't generally definitive.

Consider again the last equation of Guided Practice 3.2.38. Using the tree diagram, we can see that the numerator (the top of the fraction) is equal to the following product:

\begin{gather*} P(\text{ has BC and mammogram\(^+\) } ) = P(\text{ mammogram\(^+\) } | \text{ has BC } )P(\text{ has BC } ) \end{gather*}

The denominator — the probability the screening was positive — is equal to the sum of probabilities for each positive screening scenario:

\begin{align*} P(\text{mammogram\(^+\)} ) \amp = P(\text{mammogram\(^+\) and no BC} ) + P(\text{mammogram\(^+\) and has BC} ) \end{align*}

In the example, each of the probabilities on the right side was broken down into a product of a conditional probability and marginal probability using the tree diagram.

\begin{align*} P(\text{ mammogram\(^+\) } ) \amp = P(\text{ mammogram\(^+\) and no BC } ) + P(\text{ mammogram\(^+\) and has BC } )\\ \amp = P(\text{ mammogram\(^+\) } | \text{ no BC } )P(\text{ no BC } )\\ \amp \qquad\qquad + P(\text{ mammogram\(^+\) } | \text{ has BC } )P(\text{ has BC } ) \end{align*}

We can see an application of Bayes' Theorem by substituting the resulting probability expressions into the numerator and denominator of the original conditional probability.

\begin{align*} \amp P(\text{ has BC } | \text{ mammogram\(^+\) } )\\ \amp \qquad= \frac{P(\text{ mammogram\(^+\) } | \text{ has BC } )P(\text{ has BC } )} {P(\text{ mammogram\(^+\) } | \text{ no BC } )P(\text{ no BC } ) + P(\text{ mammogram\(^+\) } | \text{ has BC } )P(\text{ has BC } )} \end{align*}
Bayes' Theorem: inverting probabilities

Consider the following conditional probability for variable 1 and variable 2:

\begin{gather*} P(\text{ outcome \(A_1\) of variable 1 } | \text{ outcome \(B\) of variable 2 } ) \end{gather*}

Bayes' Theorem states that this conditional probability can be identified as the following fraction:

\begin{gather} \frac{P(B | A_1) P(A_1)} {P(B | A_1) P(A_1) + P(B | A_2) P(A_2) + \cdots + P(B | A_k) P(A_k)}\label{bayes}\tag{3.2.5} \end{gather}

where \(A_2\text{,}\) \(A_3\text{,}\) ..., and \(A_k\) represent all other possible outcomes of the first variable.

Bayes' Theorem is just a generalization of what we have done using tree diagrams. The formula need not be memorized, since it can always be derived using a tree diagram:

  • The numerator identifies the probability of getting both \(A_1\) and \(B\text{.}\)

  • The denominator is the overall probability of getting \(B\text{.}\) Traverse each branch of the tree diagram that ends with event \(B\text{.}\) Add up the required products.

Jose visits campus every Thursday evening. However, some days the parking garage is full, often due to college events. There are academic events on 35% of evenings, sporting events on 20% of evenings, and no events on 45% of evenings. When there is an academic event, the garage fills up about 25% of the time, and it fills up 70% of evenings with sporting events. On evenings when there are no events, it only fills up about 5% of the time. If Jose comes to campus and finds the garage full, what is the probability that there is a sporting event? Use a tree diagram to solve this problem. 31 The tree diagram, with three primary branches, is shown below. We want

\begin{align*} P(\amp \text{ sporting event } | \text{ garage full } )\\ \amp = \frac{P(\text{ sporting event and garage full } )}{P(\text{ garage full } )}\\ \amp =\frac{0.14}{0.0875 + 0.14 + 0.0225} = 0.56. \end{align*}
If the garage is full, there is a 56% probability that there is a sporting event.

The last several exercises offered a way to update our belief about whether there is a sporting event, academic event, or no event going on at the school based on the information that the parking lot was full. This strategy of updating beliefs using Bayes' Theorem is actually the foundation of an entire section of statistics called Bayesian statistics. While Bayesian statistics is very important and useful, we will not have time to cover it in this book.