Take a second look at Guided Practice 3.3.6. We asked many probability questions regarding this scenario that could be solved using the binomial formula. Instead of looking at it piecewise, we could describe the entire distribution of possible values and their corresponding probabilities. Since there are 4 smoking friends, there are several possible outcomes for the number who might develop a severe lung condition in their lifetime: 0, 1, 2, 3, 4. We can make a distribution table as we did previously. Recall that the probability that a random smoker will develop a severe lung condition in her lifetime is about \(0.3\text{.}\)
| \(x_i\) | \(p_i\) |
| 0 | \({4\choose 0}(0.3)^0(0.7)^{4} = 0.240\) |
| 1 | \({4\choose 1}(0.3)^1(0.7)^{3} = 0.412\) |
| 2 | \({4\choose 2}(0.3)^2(0.7)^{2} = 0.265\) |
| 3 | \({4\choose 3}(0.3)^3(0.7)^{1} = 0.076\) |
| 4 | \({4\choose 4}(0.3)^4(0.7)^{0} = 0.008\) |
Since this is a probability distribution we could find the mean and standard deviation of it using the formulas from Chapter 3. Those formulas require a lot of calculations, so it is fortunate that there are shortcuts for the mean and the standard deviation of a binomial random variable.
For a binomial distribution with parameters \(n\) and \(p\text{,}\) where \(n\) is the number of trials and \(p\) is the probability of a success, the mean and standard deviation of the number of observed successes are
If the probability that a random smoker will develop a severe lung condition in his or her lifetime is \(0.3\) and you have 40 smoking friends, about how many would you expect to develop such a condition? What is the standard deviation of the number of people who would develop such a condition? Equation (4.4.1) may be useful.
We are asked to determine the expected number (the mean) and the standard deviation, both of which can be directly computed from the formulas in Equation (4.4.1), as shown below. The exact distribution is shown in Figure 4.4.5.
The binomial formula is cumbersome when the sample size (\(n\)) is large, particularly when we consider a range of observations. Suppose we wanted to find the probability that at least 25 of 40 smoking friends will develop a severe lung condition. We would need to use the binomial formula with \(k=25\text{,}\) \(k=26\text{,}\) \(k=27\text{,}\) ..., \(k=40\text{.}\) That's a lot of work! In some cases we may use the normal distribution as an easier and faster way to estimate binomial probabilities. While a normal approximation for the distribution in Figure 4.4.3 would not be appropriate, it would not be too bad for the distribution in Figure 4.4.5.
Approximately 20% of the US population smokes cigarettes. A local government believed their community had a lower smoker rate and commissioned a survey of 400 randomly selected individuals. The survey found that only 60 of the 400 participants smoke cigarettes. If the true proportion of smokers in the community was really 20%, what is the probability of observing 60 or fewer smokers in a sample of 400 people?
We leave the usual verification that the four conditions for the binomial model are valid as an exercise.
The question posed is equivalent to asking, what is the probability of observing \(k=0\text{,}\) 1, ..., 59, or 60 smokers in a sample of \(n=400\) when \(p=0.20\text{?}\) We can compute these 61 different probabilities and add them together to find the answer:
If the true proportion of smokers in the community is \(p=0.20\text{,}\) then the probability of observing 60 or fewer smokers in a sample of \(n=400\) is less than 0.0061.
The computations in Example 4.4.6 are tedious and long. In general, we should avoid such work if an alternative method exists that is faster, easier, and still accurate. Recall that calculating probabilities of a range of values is much easier in the normal model. We might wonder, is it reasonable to use the normal model in place of the binomial distribution? Surprisingly, yes, if certain conditions are met.
Here we consider the binomial model when the probability of a success is \(p=0.10\text{.}\) Figure 4.4.8 shows four hollow histograms for simulated samples from the binomial distribution using four different sample sizes: \(n=10\text{,}\) 30, 100, 300. What happens to the shape of the distributions as the sample size increases? What distribution does the last hollow histogram resemble? 1 The distribution is transformed from a blocky and skewed distribution into one that rather resembles the normal distribution in last hollow histogram
The binomial distribution with probability of success \(p\) is nearly normal when the sample size \(n\) is sufficiently large that \(np\ge 10\) and \(n(1-p)\ge 10\text{.}\) The approximate normal distribution has parameters corresponding to the mean and standard deviation of the binomial distribution:
The normal approximation may be used when computing the range of many possible successes. For instance, we may apply the normal distribution to the setting described in Example 4.4.6.
Use the normal approximation to estimate the probability of observing 60 or fewer smokers in a sample of 400, if the true proportion of smokers is \(p=0.20\text{.}\)
As in Example 4.4.6, we leave it to the reader to show that the binomial model is reasonable for this context. However, we will verify that both \(np\) and \(n(1-p)\) are at least 10 so we can apply the normal model:
With these conditions checked, we may use the normal approximation in place of the binomial distribution with the following mean and standard deviation:
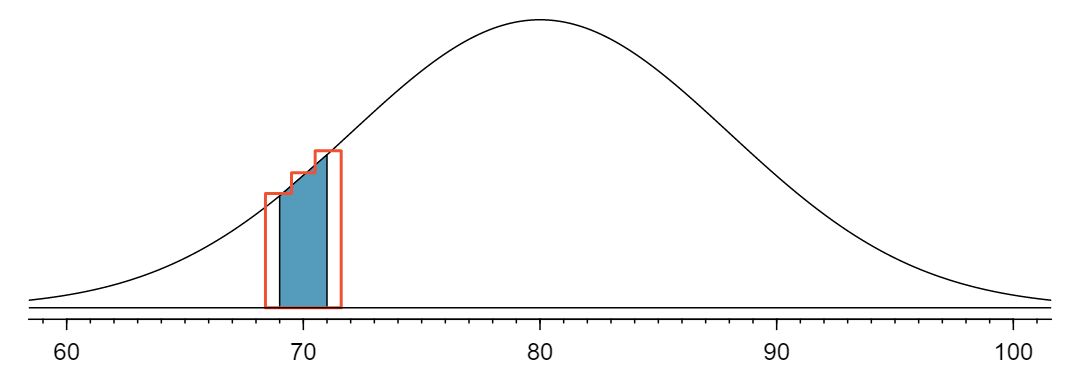
We want to find the probability of observing 60 or fewer smokers using this model. We know that this probability will be small because 60 is more than 2 standard deviations below the mean:
Next, we compute the Z-score as \(Z=\frac{60 - 80}{8} = -2.5\) to find the shaded area in the picture: \(P(Z \lt -2.5) = 0.0062\text{.}\) This probability of 0.0062 using the normal approximation is remarkably close to the true probability of 0.0061 from the binomial distribution!
The normal approximation to the binomial distribution tends to perform poorly when estimating the probability of a small range of counts, even when the conditions are met.
Suppose we wanted to compute the probability of observing 69, 70, or 71 smokers in 400 when \(p=0.20\text{.}\) With such a large sample, we might be tempted to apply the normal approximation and use the range 69 to 71. However, we would find that the binomial solution and the normal approximation notably differ:
We can identify the cause of this discrepancy using Figure 4.4.10, which shows the areas representing the binomial probability (outlined) and normal approximation (shaded). Notice that the width of the area under the normal distribution is 0.5 units too slim on both sides of the interval. The binomial distribution is a discrete distribution, and the each bar is centered over an integer value. Looking closely at Figure 4.4.10, we can see that the bar corresponding to 69 begins at 68.5 and ends at 69.5, the bar corresponding to 70 begins at 69.5 and ends at 70.5, etc.
The normal approximation to the binomial distribution for intervals of values is usually improved if cutoff values for the lower end of a shaded region are reduced by 0.5 and the cutoff value for the upper end are increased by 0.5. This correction is called the continuity correction and accounts for the fact that the binomial distribution is discrete.
Use the method described to find a more accurate estimate for the probability of observing 69, 70, or 71 smokers in 400 randomly selected people when \(p=0.20\text{.}\)
Instead of standardizing 69 and 71, we will standardize 68.5 and 71.5:
The probability 0.0687 is much closer to the true value of 0.0703 than the previous estimate of 0.0476 we calculated using normal approximation without the continuity correction.
It is always possible to apply the continuity correction when finding a normal approximation to the binomial distribution. However, when \(n\) is very large or when the interval is wide, the benefit of the modification is limited since the added area becomes negligible compared to the overall area being calculated.
