Advanced High School Statistics: First Edition

1 True or false

Determine if the statements below are true or false, and explain your reasoning.

1. If a fair coin is tossed many times and the last eight tosses are all heads, then the chance that the next toss will be heads is somewhat less than 50%. Answer

   False. These are independent trials.

2. Drawing a face card (jack, queen, or king) and drawing a red card from a full deck of playing cards are mutually exclusive events. Answer

   False. There are red face cards.

3. Drawing a face card and drawing an ace from a full deck of playing cards are mutually exclusive events. Answer

   True. A card cannot be both a face card and an ace.

2 Roulette wheel

The game of roulette involves spinning a wheel with 38 slots: 18 red, 18 black, and 2 green. A ball is spun onto the wheel and will eventually land in a slot, where each slot has an equal chance of capturing the ball.

1. You watch a roulette wheel spin 3 consecutive times and the ball lands on a red slot each time. What is the probability that the ball will land on a red slot on the next spin?

2. You watch a roulette wheel spin 300 consecutive times and the ball lands on a red slot each time. What is the probability that the ball will land on a red slot on the next spin?

3. Are you equally confident of your answers to parts (a) and (b)? Why or why not?

.jpg

3 Four games, one winner

Below are four versions of the same game. Your archnemisis gets to pick the version of the game, and then you get to choose how many times to flip a coin: 10 times or 100 times. Identify how many coin flips you should choose for each version of the game. It costs $1 to play each game. Explain your reasoning.

1. If the proportion of heads is larger than 0.60, you win $1. Answer

   10 tosses. Fewer tosses mean more variability in the sample fraction of heads, meaning there's a better chance of getting at least 60% heads.

2. If the proportion of heads is larger than 0.40, you win $1. Answer

   100 tosses. More flips means the observed proportion of heads would often be closer to the average, 0.50, and therefore also above 0.40.

3. If the proportion of heads is between 0.40 and 0.60, you win $1. Answer

   100 tosses. With more flips, the observed proportion of heads would often be closer to the average, 0.50.

4. If the proportion of heads is smaller than 0.30, you win $1. Answer

   10 tosses. Fewer flips would increase variability in the fraction of tosses that are heads.

4 Backgammon

Backgammon is a board game for two players in which the playing pieces are moved according to the roll of two dice. Players win by removing all of their pieces from the board, so it is usually good to roll high numbers. You are playing backgammon with a friend and you roll two 6s in your first roll and two 6s in your second roll. Your friend rolls two 3s in his first roll and again in his second row. Your friend claims that you are cheating, because rolling double 6s twice in a row is very unlikely. Using probability, show that your rolls were just as likely as his.

5 Coin flips

If you flip a fair coin 10 times, what is the probability of

1. getting all tails? Answer

   \(0.5^{10}\) = 0.00098.

2. getting all heads? Answer

   \(0.5^{10}\) = 0.00098.

3. getting at least one tails? Answer

   \(P\)(at least one tails) = \(1 - P\)(no tails) = \(1 - (0.5^{10}) \approx 1 - 0.001 = 0.999\text{.}\)

6 Dice rolls

If you roll a pair of fair dice, what is the probability of

1. getting a sum of 1?

2. getting a sum of 5?

3. getting a sum of 12?

7 Swing voters

A 2012 Pew Research survey asked 2,373 randomly sampled registered voters their political affiliation (Republican, Democrat, or Independent) and whether or not they identify as swing voters. 35% of respondents identified as Independent, 23% identified as swing voters, and 11% identified as both.¹Pew Research Center, With Voters Focused on Economy, Obama Lead Narrows, data collected between April 4-15, 2012.

1. Are being Independent and being a swing voter disjoint, i.e. mutually exclusive? Answer

   No, there are voters who are both politically Independent and also swing voters.

2. Draw a Venn diagram summarizing the variables and their associated probabilities. Answer

   Venn diagram below:

   
3. What percent of voters are Independent but not swing voters? Answer

   24%.

4. What percent of voters are Independent or swing voters? Answer

   Add up the corresponding disjoint sections in the Venn diagram: \(0.24 + 0.11 + 0.12 = 0.47\text{.}\) Alternatively, use the General Addition Rule: \(0.35 + 0.23 - 0.11 = 0.47\text{.}\)

5. What percent of voters are neither Independent nor swing voters? Answer

   \(1 - 0.47 = 0.53\text{.}\)

6. Is the event that someone is a swing voter independent of the event that someone is a political Independent? Answer

   \(P\)(Independent) \(\times\) \(P\)(swing) = \(0.35\times0.23 = 0.08\text{,}\) which does not equal P(Independent and swing) = 0.11, so the events are dependent. If you stated that this difference might be due to sampling variability in the survey, that answer would also be reasonable (we'll dive into this topic more in later chapters).

8 Poverty and language

The American Community Survey is an ongoing survey that provides data every year to give communities the current information they need to plan investments and services. The 2010 American Community Survey estimates that 14.6% of Americans live below the poverty line, 20.7% speak a language other that English at home, and 4.2% fall into both categories.²U.S. Census Bureau, 2010 American Community Survey 1-Year Estimates, Characteristics of People by Language Spoken at Home

1. Are living below the poverty line and speaking a language other than English at home disjoint?

2. Draw a Venn diagram summarizing the variables and their associated probabilities.

3. What percent of Americans live below the poverty line and only speak English at home?

4. What percent of Americans live below the poverty line or speak a language other than English at home?

5. What percent of Americans live above the poverty line and only speak English at home?

6. Is the event that someone lives below the poverty line independent of the event that the person speaks a language other than English at home?

9 Disjoint vs. independent

In parts (a) and (b), identify whether the events are disjoint, independent, or neither (events cannot be both disjoint and independent).

1. You and a randomly selected student from your class both earn A's in this course. Answer

   If the class is not graded on a curve, they are independent. If graded on a curve, then neither independent nor disjoint (unless the instructor will only give one A, which is a situation we will ignore in parts (b) and (c)).

2. You and your class study partner both earn A's in this course. Answer

   They are probably not independent: if you study together, your study habits would be related, which suggests your course performances are also related.

3. If two events can occur at the same time, must they be dependent? Answer

   No. See the answer to part (a) when the course is not graded on a curve. More generally: if two things are unrelated (independent), then one occurring does not preclude the other from occurring.

10 Guessing on an exam

In a multiple choice exam, there are 5 questions and 4 choices for each question (a, b, c, d). Nancy has not studied for the exam at all and decides to randomly guess the answers. What is the probability that:

1. the first question she gets right is the \(5^{th}\) question?

2. she gets all of the questions right?

3. she gets at least one question right?

11 Educational attainment of couples

The table below shows the distribution of education level attained by US residents by gender based on data collected during the 2010 American Community Survey.³U.S. Census Bureau, 2010 American Community Survey 1-Year Estimates, Educational Attainment.

1. What is the probability that a randomly chosen man has at least a Bachelor's degree? Answer

   \(0.16 + 0.09 = 0.25\text{.}\)

2. What is the probability that a randomly chosen woman has at least a Bachelor's degree? Answer

   \(0.17 + 0.09 = 0.26\text{.}\)

3. What is the probability that a man and a woman getting married both have at least a Bachelor's degree? Note any assumptions you must make to answer this question. Answer

   Assuming that the education level of the husband and wife are independent: \(0.25 \times 0.26 = 0.065\text{.}\) You might also notice we actually made a second assumption: that the decision to get married is unrelated to education level.

4. If you made an assumption in part (c), do you think it was reasonable? If you didn't make an assumption, double check your earlier answer and then return to this part. Answer

   The husband/wife independence assumption is probably not reasonable, because people often marry another person with a comparable level of education. We will leave it to you to think about whether the second assumption noted in part (c) is reasoanble.

12 School absences

Data collected at elementary schools in DeKalb County, GA suggest that each year roughly 25% of students miss exactly one day of school, 15% miss 2 days, and 28% miss 3 or more days due to sickness.⁴S.S. Mizan et al. "Absence, Extended Absence, and Repeat Tardiness Related to Asthma Status among Elementary School Children". In: Journal of Asthma 48.3 (2011), pp. 228-234.

1. What is the probability that a student chosen at random doesn't miss any days of school due to sickness this year?

2. What is the probability that a student chosen at random misses no more than one day?

3. What is the probability that a student chosen at random misses at least one day?

4. If a parent has two kids at a DeKalb County elementary school, what is the probability that neither kid will miss any school? Note any assumption you must make to answer this question.

5. If a parent has two kids at a DeKalb County elementary school, what is the probability that both kids will miss some school, i.e. at least one day? Note any assumption you make.

6. If you made an assumption in part (d) or (e), do you think it was reasonable? If you didn't make any assumptions, double check your earlier answers.

13 Grade distributions

Each row in the table below is a proposed grade distribution for a class. Identify each as a valid or invalid probability distribution, and explain your reasoning.

14 Health and health coverage, Part I

The Behavioral Risk Factor Surveillance System (BRFSS) is an annual telephone survey designed to identify risk factors in the adult population and report emerging health trends. The following table summarizes two variables for the respondents: health status and health coverage, which describes whether each respondent had health insurance.⁵Office of Surveillance, Epidemiology, and Laboratory Services Behavioral Risk Factor Surveillance System, DEAD LINK? BRFSS 2010 Survey Data

1. If we draw one individual at random, what is the probability that the respondent has excellent health and doesn't have health coverage?

2. If we draw one individual at random, what is the probability that the respondent has excellent health or doesn't have health coverage?

15 Joint and conditional probabilities

P(A) = 0.3, P(B) = 0.7

1. Can you compute P(A and B) if you only know P(A) and P(B)? Answer

   No, but we could if A and B are independent.

2. Assuming that events A and B arise from independent random processes, LIST ISSUE what is P(A and B)? Answer 1

   0.21.

   what is P(A or B)? Answer 2

   \(0.3+0.7-0.21=0.79\text{.}\)

   what is P(A\(|\)B)? Answer 3

   Same as \(P(A)\text{:}\) 0.3.

3. If we are given that P(A and B) = 0.1, are the random variables giving rise to events A and B independent? Answer

   No, because 0.1 \(\ne\) 0.21, where 0.21 was the value computed under independence from part (a).

4. If we are given that P(A and B) = 0.1, what is P(A\(|\)B)? Answer

   \(P(\)A\(|\)B\() = 0.1 / 0.7 = 0.143\text{.}\)

16 PB & J

Suppose 80% of people like peanut butter, 89% like jelly, and 78% like both. Given that a randomly sampled person likes peanut butter, what's the probability that he also likes jelly?

17 Global warming

A 2010 Pew Research poll asked 1,306 Americans “From what you've read and heard, is there solid evidence that the average temperature on earth has been getting warmer over the past few decades, or not?”. The table below shows the distribution of responses by party and ideology, where the counts have been replaced with relative frequencies.⁶CITE

1. Are being the earth is warming and being a liberal Democrat mutually exclusive? Answer

   No, these events are not mutually exclusive, there are people who believe the earth is warming and are liberal Democrats.

2. What is the probability that a randomly chosen respondent believes the earth is warming or is a liberal Democrat? Answer

   \(0.60 + 0.20 - 0.18 = 0.62\text{.}\)

3. What is the probability that a randomly chosen respondent believes the earth is warming given that he is a liberal Democrat? Answer

   \(0.18/0.20 = 0.90\text{.}\)

4. What is the probability that a randomly chosen respondent believes the earth is warming given that he is a conservative Republican? Answer

   \(0.11/0.33 \approx 0.33\text{.}\)

5. Does it appear that whether or not a respondent believes the earth is warming is independent of their party and ideology? Explain your reasoning. Answer

   No, otherwise the final answers of parts (b) and (c) would have been equal

6. What is the probability that a randomly chosen respondent is a moderate/liberal Republican given that he does not believe that the earth is warming? Answer

   \(0.06/0.34 \approx 0.18\text{.}\)

18 Health and health coverage, Part II

Health coverage part I Introduced a contingency table summarizing the relationship between health status and health coverage for a sample of 20,000 Americans. In the table below, the counts have been replaced by relative frequencies (probability estimates).

1. Are being in excellent health and having health coverage mutually exclusive?

2. What is the probability that a randomly chosen individual has excellent health?

3. What is the probability that a randomly chosen individual has excellent health given that he has health coverage?

4. What is the probability that a randomly chosen individual has excellent health given that he doesn't have health coverage?

5. Do having excellent health and having health coverage appear to be independent?

19 Burger preferences

A 2010 SurveyUSA poll asked 500 Los Angeles residents, “What is the best hamburger place in Southern California? Five Guys Burgers? In-N-Out Burger? Fat Burger? Tommy's Hamburgers? Umami Burger? Or somewhere else?” The distribution of responses by gender is shown below.⁷SurveyUSA, Results of SurveyUSA News Poll #17718, data collected on December 2, 2010

1. Are being female and liking Five Guys Burgers mutually exclusive? Answer

   No, these events are not mutually exclusive, there are females who like Five Guys Burgers.

2. What is the probability that a randomly chosen male likes In-N-Out the best? Answer

   \(162/248 = 0.65\text{.}\)

3. What is the probability that a randomly chosen female likes In-N-Out the best? Answer

   \(181/252 = 0.72\)

4. What is the probability that a man and a woman who are dating both like In-N-Out the best? Note any assumption you make and evaluate whether you think that assumption is reasonable. Answer

   Under the assumption of a dating choices being independent of hamburger preference, which on the surface seems reasonable: \(0.65 \times 0.72 = 0.468\text{.}\)

5. What is the probability that a randomly chosen person likes Umami best or that person is female? Answer

   \((252 + 6 - 1)/500 = 0.514\)

20 Assortative mating

Assortative mating is a nonrandom mating pattern where individuals with similar genotypes and/or phenotypes mate with one another more frequently than what would be expected under a random mating pattern. Researchers studying this topic collected data on eye colors of 204 Scandinavian men and their female partners. The table below summarizes the results. For simplicity, we only include heterosexual relationships in this exercise.⁸B. Laeng et al. \Why do blue-eyed men prefer women with the same eye color?"In: Behavioral Ecology and Sociobiology 61.3 (2007), pp. 371-384.

1. What is the probability that a randomly chosen male respondent or his partner has blue eyes?

2. What is the probability that a randomly chosen male respondent with blue eyes has a partner with blue eyes?

3. What is the probability that a randomly chosen male respondent with brown eyes has a partner with blue eyes? What about the probability of a randomly chosen male respondent with green eyes having a partner with blue eyes?

4. Does it appear that the eye colors of male respondents and their partners are independent? Explain your reasoning.

21 Urns and marbles, Part I

Imagine you have an urn containing 5 red, 3 blue, and 2 orange marbles in it.

1. What is the probability that the first marble you draw is blue? Answer

   0.3.

2. Suppose you drew a blue marble in the first draw. If drawing with replacement, what is the probability of drawing a blue marble in the second draw? Answer

   0.3.

3. Suppose you instead drew an orange marble in the first draw. If drawing with replacement, what is the probability of drawing a blue marble in the second draw? Answer

   0.3.

4. If drawing with replacement, what is the probability of drawing two blue marbles in a row? Answer

   \(0.3\times0.3=0.09\text{.}\)

5. When drawing with replacement, are the draws independent? Explain. Answer

   Yes, the population that is being sampled from is identical in each draw.

22 Socks in a drawer

In your sock drawer you have 4 blue, 5 gray, and 3 black socks. Half asleep one morning you grab 2 socks at random and put them on. Find the probability you end up wearing

1. 2 blue socks

2. no gray socks

3. at least 1 black sock

4. a green sock

5. matching socks

23 Urns and marbles, Part II

Imagine you have an urn containing 5 red, 3 blue, and 2 orange marbles.

1. Suppose you draw a marble and it is blue. If drawing without replacement, what is the probability the next is also blue? Answer

   2/9.

2. Suppose you draw a marble and it is orange, and then you draw a second marble without replacement. What is the probability this second marble is blue? Answer

   \(3/9=1/3\text{.}\)

3. If drawing without replacement, what is the probability of drawing two blue marbles in a row? Answer

   \((3/10)\times(2/9) \approx 0.067\text{.}\)

4. When drawing without replacement, are the draws independent? Explain. Answer

   No. In this small population of marbles, removing one marble meaningfully changes the probability of what might be drawn next.

24 Books on a bookshelf

The table below shows the distribution of books on a bookcase based on whether they are nonfiction or fiction and hardcover or paperback.

1. Find the probability of drawing a hardcover book first then a paperback fiction book second when drawing without replacement.

2. Determine the probability of drawing a fiction book first and then a hardcover book second, when drawing without replacement.

3. Calculate the probability of the scenario in part (b), except this time complete the calculations under the scenario where the first book is placed back on the bookcase before randomly drawing the second book.

4. The final answers to parts (b) and (c) are very similar. Explain why this is the case.

25 Student outfits

In a classroom with 24 students, 7 students are wearing jeans, 4 are wearing shorts, 8 are wearing skirts, and the rest are wearing leggings. If we randomly select 3 students without replacement, what is the probability that one of the selected students is wearing leggings and the other two are wearing jeans? Note that these are mutually exclusive clothing options.

26 The birthday problem

Suppose we pick three people at random. For each of the following questions, ignore the special case where someone might be born on February 29th, and assume that births are evenly distributed throughout the year.

1. What is the probability that the first two people share a birthday?

2. What is the probability that at least two people share a birthday?

27 Drawing box plots

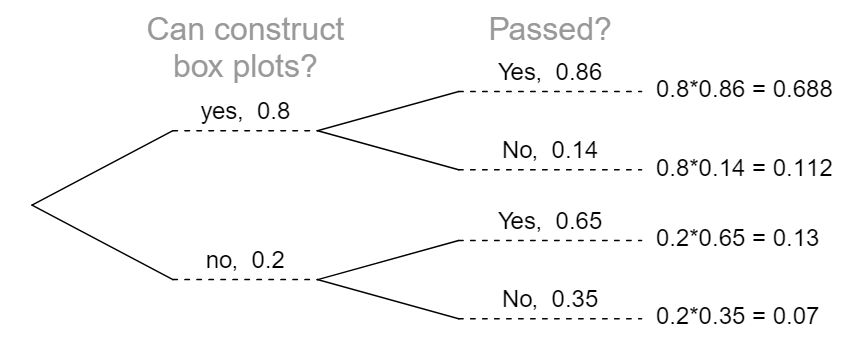
After an introductory statistics course, 80% of students can successfully construct box plots. Of those who can construct box plots, 86% passed, while only 65% of those students who could not construct box plots passed.

1. Construct a tree diagram of this scenario. Answer

   The tree diagram:

   
2. Calculate the probability that a student is able to construct a box plot if it is known that he passed. Answer

   \(P(\text{\scriptsize canconstruct} | \text{\scriptsize pass}) = \frac{P(\text{\scriptsize canconstructandpass})}{P(\text{\scriptsize pass})}\) \(= \frac{0.8 \times 0.86}{0.8 \times 0.86+0.2 \times 0.65} = \frac{0.688}{0.818} \approx 0.84\text{.}\)

28 Predisposition for thrombosis

A genetic test is used to determine if people have a predisposition for thrombosis, which is the formation of a blood clot inside a blood vessel that obstructs the flow of blood through the circulatory system. It is believed that 3% of people actually have this predisposition. The genetic test is 99% accurate if a person actually has the predisposition, meaning that the probability of a positive test result when a person actually has the predisposition is 0.99. The test is 98% accurate if a person does not have the predisposition. What is the probability that a randomly selected person who tests positive for the predisposition by the test actually has the predisposition?

29 HIV in Swaziland

Swaziland has the highest HIV prevalence in the world: 25.9% of this country's population is infected with HIV.⁹Source: CIA Factbook, Country Comparison: HIV/AIDS - Adult Prevalence Rate.The ELISA test is one of the first and most accurate tests for HIV. For those who carry HIV, the ELISA test is 99.7% accurate. For those who do not carry HIV, the test is 92.6% accurate. If an individual from Swaziland has tested positive, what is the probability that he carries HIV?

First draw a tree diagram:

Then compute the probability: \(P(HIV | +) = \frac{P(HIVand+)}{P(+)} = \frac{0.259 \times 0.997}{0.259 \times 0.997 + 0.741 \times 0.074}= \frac{0.2582}{0.3131} = 0.8247\text{.}\)

30 Exit poll

Edison Research gathered exit poll results from several sources for the Wisconsin recall election of Scott Walker. They found that 53% of the respondents voted in favor of Scott Walker. Additionally, they estimated that of those who did vote in favor for Scott Walker, 37% had a college degree, while 44% of those who voted against Scott Walker had a college degree. Suppose we randomly sampled a person who participated in the exit poll and found that he had a college degree. What is the probability that he voted in favor of Scott Walker?¹⁰New York Times, Wisconsin recall exit polls.

31 It's never lupus

Lupus is a medical phenomenon where antibodies that are supposed to attack foreign cells to prevent infections instead see plasma proteins as foreign bodies, leading to a high risk of blood clotting. It is believed that 2% of the population suffer from this disease. The test is 98% accurate if a person actually has the disease. The test is 74% accurate if a person does not have the disease. There is a line from the Fox television show House that is often used after a patient tests positive for lupus: “It's never lupus.” Do you think there is truth to this statement? Use appropriate probabilities to support your answer.

A tree diagram of the situation:

\(P(\text{lupus} | \text{positive}) = \frac{P(\text{\text{lupusandpositive}})}{P(\text{positive})} = \frac{0.0196}{0.0196 + 0.2548} = 0.0714\text{.}\) Even when a patient tests positive for lupus, there is only a 7.14% chance that he actually has lupus. While House is not exactly right -- it is possible that the patient has lupus -- his implied skepticism is warranted.

32 Twins

About 30% of human twins are identical, and the rest are fraternal. Identical twins are necessarily the same sex — half are males and the other half are females. One-quarter of fraternal twins are both male, one-quarter both female, and one-half are mixes: one male, one female. You have just become a parent of twins and are told they are both girls. Given this information, what is the probability that they are identical?

33 Exploring combinations

The formula for the number of ways to arrange \(n\) objects is \(n! = n\times(n-1)\times \cdots \times 2 \times 1\text{.}\) This exercise walks you through the derivation of this formula for a couple of special cases.

A small company has five employees: Anna, Ben, Carl, Damian, and Eddy. There are five parking spots in a row at the company, none of which are assigned, and each day the employees pull into a random parking spot. That is, all possible orderings of the cars in the row of spots are equally likely.

1. On a given day, what is the probability that the employees park in alphabetical order? Answer

   \(\stackrel{Anna}{1/5}\times\stackrel{Ben}{1/4}\times\stackrel{Carl}{1/3}\times\stackrel{Damian}{1/2}\times\stackrel{Eddy}{1/1} = 1/5!=1/120\text{.}\)

2. If the alphabetical order has an equal chance of occurring relative to all other possible orderings, how many ways must there be to arrange the five cars? Answer

   Since the probabilities must add to 1, there must be \(5!=120\) possible orderings.

3. Now consider a sample of 8 employees instead. How many possible ways are there to order these 8 employees' cars? Answer

   \(8!=\text{40,320}\text{.}\)

34 Male children

While it is often assumed that the probabilities of having a boy or a girl are the same, the actual probability of having a boy is slightly higher at 0.51. Suppose a couple plans to have 3 kids.

1. Use the binomial model to calculate the probability that two of them will be boys.

2. Write out all possible orderings of 3 children, 2 of whom are boys. Use these scenarios to calculate the same probability from part (a) but using the Addition Rule for disjoint events. Confirm that your answers from parts (a) and (b) match.

3. If we wanted to calculate the probability that a couple who plans to have 8 kids will have 3 boys, briefly describe why the approach from part (b) would be more tedious than the approach from part (a).

35 Underage drinking, Part I

The Substance Abuse and Mental Health Services Administration estimated that 70% of 18-20 year olds consumed alcoholic beverages in 2008.¹¹SAMHSA, Office of Applied Studies, National Survey on Drug Use and Health, 2007 and 2008.

1. Suppose a random sample of ten 18-20 year olds is taken. Is the use of the binomial distribution appropriate for calculating the probability that exactly six consumed alcoholic beverages? Explain. Answer

   Yes. The conditions are satisfied: independence, fixed number of trials, either success or failure for each trial, and probability of success being constant across trials.

2. Calculate the probability that exactly 6 out of 10 randomly sampled 18-20 year olds consumed an alcoholic drink. Answer

   0.200.

3. What is the probability that exactly 4 out of the ten 18-20 year olds have not consumed an alcoholic beverage? Answer

   0.200.

4. What is the probability that at most 2 out of 5 randomly sampled 18-20 year olds have consumed alcoholic beverages? Answer

   \(0.0024 + 0.0284 + 0.1323 = 0.1631\text{.}\)

5. What is the probability that at least 1 out of 5 randomly sampled 18-20 year olds have consumed alcoholic beverages? Answer

   \(1-0.0024 = 0.9976\text{.}\)

36 Chickenpox, Part I

The National Vaccine Information Center estimates that 90% of Americans have had chickenpox by the time they reach adulthood.¹²National Vaccine Information Center, Chickenpox, The Disease & The Vaccine Fact Sheet

1. Suppose we take a random sample of 100 American adults. Is the use of the binomial distribution appropriate for calculating the probability that exactly 97 had chickenpox before they reached adulthood? Explain.

2. Calculate the probability that exactly 97 out of 100 randomly sampled American adults had chickenpox during childhood.

3. What is the probability that exactly 3 out of a new sample of 100 American adults have not had chickenpox in their childhood?

4. What is the probability that at least 1 out of 10 randomly sampled American adults have had chickenpox?

5. What is the probability that at most 3 out of 10 randomly sampled American adults have not had chickenpox?

37 Smog check, Part I

Suppose 16% of cars fail pollution tests (smog checks) in California. We would like to estimate the probability that an entire fleet of seven cars would pass using a simulation. We assume each car is independent. We only want to know if the entire fleet passed, i.e. none of the cars failed. What is wrong with each of the following simulations to represent whether an entire (simulated) fleet passed?

1. Flip a coin seven times where each toss represents a car. A head means the car passed and a tail means it failed. If all cars passed, we report PASS for the fleet. If at least one car failed, we report FAIL. Answer

   P(pass) = 0.5

2. Read across a random number table starting at line 5. If a number is a 0 or 1, let it represent a failed car. Otherwise the car passes. We report PASS if all cars passed and FAIL otherwise. Answer

   P(pass) = 0.2

3. Read across a random number table, looking at two digits for each simulated car. If a pair is in the range [00-16], then the corresponding car failed. If it is in [17-99], the car passed. We report PASS if all cars passed and FAIL otherwise. Answer

   P(pass) = 0.17

38 Left-handed

Studies suggest that approximately 10% of the world population is left-handed. Use ten simulations to answer each of the following questions. For each question, describe your simulation scheme clearly.

1. What is the probability that at least one out of eight people are left-handed?

2. On average, how many people would you have to sample until the first person who is left-handed?

3. On average, how many left-handed people would you expect to find among a random sample of six people?

39 Smog check, Part II

Consider the fleet of seven cars in Exercise 3.7.37. Remember that 16% of cars fail pollution tests (smog checks) in California, and that we assume each car is independent.

1. Write out how to calculate the probability of the fleet failing, i.e. at least one of the cars in the fleet failing, via simulation. Answer

   Starting at row 3 of the random number table, we will read across the table two digits at a time. If the random number is between 00-15, the car will fail the pollution test. If the number is between 16-99, the car will pass the test. (Answers may vary.)

2. Simulate 5 fleets. Based on these simulations, estimate the probability at least one car will fail in a fleet. Answer

   Fleet 1: 18-52-97-32-85-95-29 \(\rightarrow\) P-P-P-P-P-P-P \(\rightarrow\) fleet passes \Fleet 2: 14-96-06-67-17-49-59 \(\rightarrow\) F-P-F-P-P-P-P \(\rightarrow\) fleet fails \Fleet 3: 05-33-67-97-58-11-81 \(\rightarrow\) F-P-P-P-P-F-P \(\rightarrow\) fleet fails \Fleet 4: 23-81-83-21-71-08-50 \(\rightarrow\) P-P-P-P-P-F-P \(\rightarrow\) fleet fails \Fleet 5: 82-84-39-31-83-14-34 \(\rightarrow\) P-P-P-P-P-F-P \(\rightarrow\) fleet fails

3. Compute the probability at least one car fails in a fleet of seven. Answer

   4 / 5 = 0.80

40 To catch a thief

Suppose that at a retail store, \(1/5^{th}\) of all employees steal some amount of merchandise. The stores would like to put an end to this practice, and one idea is to use lie detector tests to catch and fire thieves. However, there is a problem: lie detectors are not 100% accurate. Suppose it is known that a lie detector has a failure rate of 25%. A thief will slip by the test 25% of the time and an honest employee will only pass 75% of the time.

1. Describe how you would simulate whether an employee is honest or is a thief using a random number table. Write your simulation very carefully so someone else can read it and follow the directions exactly.

2. Using a random number table, simulate 20 employees working at this store and determine if they are honest or not. Make sure to record the random digits assigned to each employee as you will refer back to these in part (c).

3. Determine the result of the lie detector test for each simulated employee from part (b) using a new simulation scheme.

4. How many of these employees are “honest and passed” and how many are “honest and failed”?

5. How many of these employees are “thief and passed” and how many are “thief and failed”?

6. Suppose the management decided to fire everyone who failed the lie detector test. What percent of fired employees were honest? What percent of not fired employees were thieves?

41 College smokers

At a university, 13% of students smoke.

1. Calculate the expected number of smokers in a random sample of 100 students from this university. Answer

   If 13% of the students smoke, then we expect about \(0.13 \times 100 = 13\) to smoke in the sample.

2. The university gym opens at 9am on Saturday mornings. One Saturday morning at 8:55am there are 27 students outside the gym waiting for it to open. Should you use the same approach from part (a) to calculate the expected number of smokers among these 27 students? Answer

   No, since this is not a random sample of students, so it may not be representative with respect to smoking behavior.

42 Card game

Consider the following card game with a well-shuffled deck of cards. If you draw a red card, you win nothing. If you get a spade, you win $5. For any club, you win $10 plus an extra $20 for the ace of clubs.

1. Create a probability model for the amount you win at this game. Also, find the expected winnings for a single game and the standard deviation of the winnings.

2. What is the maximum amount you would be willing to pay to play this game? Explain.

43 Another card game

In a new card game, you start with a well-shuffled full deck and draw 3 cards without replacement. If you draw 3 hearts, you win $50. If you draw 3 black cards, you win $25. For any other draws, you win nothing.

1. Create a probability model for the amount you win at this game, and find the expected winnings. Also compute the standard deviation of this distribution. Answer

   TABLE ISSUE The table below summarizes the probability model:

2. If the game costs $5 to play, what would be the expected value and standard deviation of the net profit (or loss)? (Hint: profit = winnings \(-\) cost; \(X-5\)) Answer

   \(E(X - 5) = E(X) - 5 = 3.59 - 5 = -1.41\text{.}\) The standard deviation is the same as the standard deviation of \(X\text{:}\) $9.64.

3. If the game costs $5 to play, should you play this game? Explain. Answer

   No. The expected earnings is negative, so on average you would lose money playing the game.

44 Is it worth it?

Andy is always looking for ways to make money fast. Lately, he has been trying to make money by gambling. Here is the game he is considering playing: The game costs $2 to play. He draws a card from a deck. If he gets a number card (2-10), he wins nothing. For any face card (jack, queen or king), he wins $3. For any ace, he wins $5, and he wins an extra $20 if he draws the ace of clubs.

1. Create a probability model and find Andy's expected profit per game.

2. Would you recommend this game to Andy as a good way to make money? Explain.

45 Portfolio return

A portfolio's value increases by 18% during a financial boom and by 9% during normal times. It decreases by 12% during a recession. What is the expected return on this portfolio if each scenario is equally likely?

46 A game of roulette

The game of roulette involves spinning a wheel with 38 slots: 18 red, 18 black, and 2 green. A ball is spun onto the wheel and will eventually land in a slot, where each slot has an equal chance of capturing the ball. Gamblers can place bets on red or black. If the ball lands on their color, they double their money. If it lands on another color, they lose their money. Suppose you bet $1 on red. What's the expected value and standard deviation of your winnings?

47 A game of roulette, Part II

Exercise 3.7.46 describes winnings on a game of roulette.

1. Suppose you play roulette and bet $3 on a single round. What is the expected value and standard deviation of your total winnings? Answer

   Expected: -$0.16. Variance: 8.95. SD: $2.99.

2. Suppose you bet $1 in three different rounds. What is the expected value and standard deviation of your total winnings? Answer

   Expected: -$0.16. SD: $1.73.

3. How do your answers to parts (a) and (b) compare? What does this say about the riskiness of the two games? Answer

   Expected values are the same, but the SDs differ. The SD from the game with tripled winnings/losses is larger, since the three independent games might go in different directions (e.g. could win one game and lose two games). So the three independent games is lower risk, but in this context it just means we are likely to lose a more stable amount since the expected value is still negative.

48 Baggage fees

An airline charges the following baggage fees: $25 for the first bag and $35 for the second. Suppose 54% of passengers have no checked luggage, 34% have one piece of checked luggage and 12% have two pieces. We suppose a negligible portion of people check more than two bags.

1. Build a probability model, compute the average revenue per passenger, and compute the corresponding standard deviation.

2. About how much revenue should the airline expect for a flight of 120 passengers? With what standard deviation? Note any assumptions you make and if you think they are justified.

49 Dodgers vs. Padres

You and your friend decide to bet on the Major League Baseball game happening one evening between the Los Angeles Dodgers and the San Diego Padres. Suppose current statistics indicate that the Dodgers have a 0.46 probability of winning this game against the Padres. If your friend bets you $5 that the Dodgers will win, how much would you need to bet on the Padres to make this a fair game?

50 Selling on Ebay

Marcie has been tracking the following two items on Ebay:

• A textbook that sells for an average of $110 with a standard deviation of $4.

• Mario Kart for the Nintendo Wii, which sells for an average of $38 with a standard deviation of $5.

1. Marcie wants to sell the video game and buy the textbook. How much net money (profits - losses) would she expect to make or spend? Also compute the standard deviation of how much she would make or spend.

2. Lucy is selling the textbook on Ebay for a friend, and her friend is giving her a 10% commission (Lucy keeps 10% of the revenue). How much money should she expect to make? With what standard deviation?

51 Cost of breakfast

Sally gets a cup of coffee and a muffin every day for breakfast from one of the many coffee shops in her neighborhood. She picks a coffee shop each morning at random and independently of previous days. The average price of a cup of coffee is $1.40 with a standard deviation of 30 cents ($0.30), the average price of a muffin is $2.50 with a standard deviation of 15 cents, and the two prices are independent of each other.

1. What is the mean and standard deviation of the amount she spends on breakfast daily? Answer

   Expected: $3.90. SD: $0.34.

2. What is the mean and standard deviation of the amount she spends on breakfast weekly (7 days)? Answer

   Expected: $27.30. SD: $0.89. If you computed part (b) using part (a), you should have obtained an SD of $0.90.

52 Ice cream

Ice cream usually comes in 1.5 quart boxes (48 fluid ounces), and ice cream scoops hold about 2 ounces. However, there is some variability in the amount of ice cream in a box as well as the amount of ice cream scooped out. We represent the amount of ice cream in the box as \(X\) and the amount scooped out as \(Y\text{.}\) Suppose these random variables have the following means, standard deviations, and variances:

1. An entire box of ice cream, plus 3 scoops from a second box is served at a party. How much ice cream do you expect to have been served at this party? What is the standard deviation of the amount of ice cream served?

2. How much ice cream would you expect to be left in the box after scooping out one scoop of ice cream? That is, find the expected value of \(X-Y\text{.}\) What is the standard deviation of the amount left in the box?

3. Using the context of this exercise, explain why we add variances when we subtract one random variable from another.

53 Cat weights

The histogram shown below represents the weights (in kg) of 47 female and 97 male cats.¹³W. N. Venables and B. D. Ripley. Modern Applied Statistics with S. Fourth Edition. www.stats.ox.ac.uk/pub/MASS4. New York: Springer, 2002.

1. What fraction of these cats weigh less than 2.5 kg? Answer

   Approximate answers are OK. Answers are only estimates based on the sample. (a) \((29+32)/144 = 0.42\text{.}\)

2. What fraction of these cats weigh between 2.5 and 2.75 kg? Answer

   \(21/144 = 0.15\text{.}\)

3. What fraction of these cats weigh between 2.75 and 3.5 kg? Answer

   \((26+12+15)/144 = 0.37\text{.}\)

54 Income and gender

The relative frequency table below displays the distribution of annual total personal income (in 2009 inflation-adjusted dollars) for a representative sample of 96,420,486 Americans. These data come from the American Community Survey for 2005-2009. This sample is comprised of 59% males and 41% females.¹⁴U.S. Census Bureau, 2005-2009 American Community Survey.

1. Describe the distribution of total personal income.

2. What is the probability that a randomly chosen US resident makes less than $50,000 per year?

3. What is the probability that a randomly chosen US resident makes less than $50,000 per year and is female? Note any assumptions you make.

4. The same data source indicates that 71.8% of females make less than $50,000 per year. Use this value to determine whether or not the assumption you made in part (c) is valid.