Section 8.5 Transformations for nonlinear data
Subsection 8.5.1 Untransformed
Consider the scatterplot and residual plot in Figure 8.5.2. The regression output is also provided. Would a linear model be a good model for the data shown?
First, we can note the \(R^2\) value is fairly large. However, this alone does not mean that the model is good. Another model might be much better. When assessing the appropriateness of a linear model, we should look at the residual plot. The U pattern in the residual plot tells us the original data is curved. If we inspect the two plots, we can see that for small and large values of \(x\) we systematically underestimate \(y\text{,}\) whereas for middle values of \(x\text{,}\) we systematically overestimate \(y\text{.}\) Because of this, the model is not appropriate, and we should not carry out a linear regression \(t\)-test because the conditions for inference are not met. However, we might be able to use a transformation to linearize the data.

The regression equation is: y = -52.3564 + 2.7842 x Predictor Coef SE Coef T P Constant -52.3564 7.2757 -7.196 3e-08 x 2.7842 0.1768 15.752 < 2e-16 S = 13.76 R-Sq = 88.26% R-Sq(adj) = 87.91%
Subsection 8.5.2 Transformed
Regression analysis is easier to perform on linear data. When data are nonlinear, we sometimes transform the data in a way that makes the resulting relationship linear. The most common transformation is log (or ln) of the \(y\) values. Sometimes we also apply a transformation to the \(x\) values. We generally use the residuals as a way to evaluate whether the transformed data are more linear. If so, we can say that a better model has been found.
Example 8.5.3
Using the regression output for the transformed data, write the new linear regression equation
\(\widehat{log(y)} = 1.723 +0.053 x\)
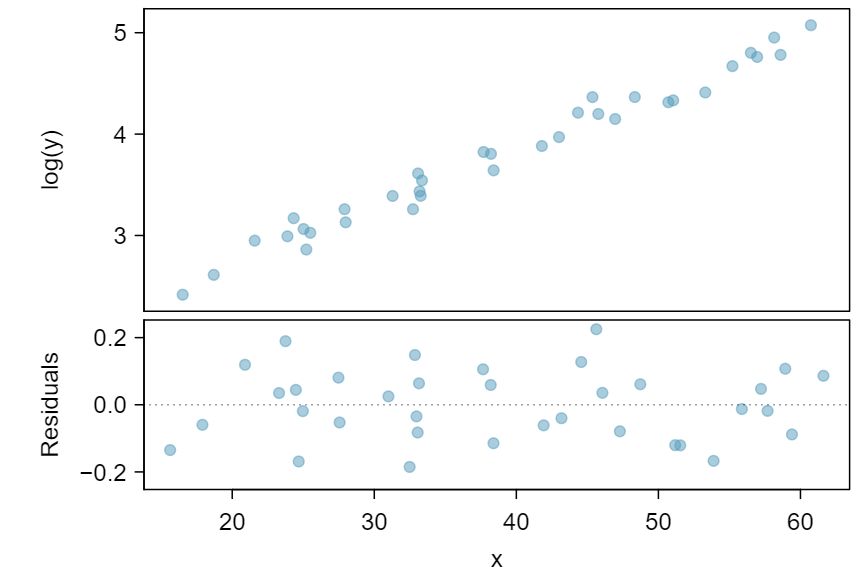
The regression equation is:
log(y) = 1.722540 + 0.052985 x
Predictor Coef SE Coef T P
Constant 1.722540 0.056731 30.36 < 2e-16
x 0.052985 0.001378 38.45 < 2e-16
S = 0.1073 R-Sq = 97.82% R-Sq(adj) = 97.75%
Guided Practice 8.5.5
Which of the following statements are true? There may be more than one. 1 Part (a) is false since there is a nonlinear (curved) trend in the data. Part (b) is true. Since the transformed data shows a stronger linear trend, it is a better fit, i.e. Part (c) is false, and Part (d) is true.
There is an apparent linear relationship between \(x\) and \(y\text{.}\)
There is an apparent linear relationship between \(x\) and \(\widehat{log(y)}\text{.}\)
The model provided by Regression I (\(\hat{y} = -52.3564 + 2.7842 x\)) yields a better fit.
The model provided by Regression II (\(\widehat{log(y)} = 1.723 +0.053 x\)) yields a better fit.
