Section2.1Variables and Evaluating Expressions
¶A key sign that you are moving on from arithmetic to algebra is if you are using variables, discussed in this section. Any combination of numbers and variables using mathematical operations is called a mathematical expression. Some expressions are simple, and some are complicated. Some expressions are abstract, whereas some have context and meaning. One example of a simple expression with context is \(220 - a\text{,}\) which has one variable, \(a\text{,}\) and is the expression for the maximum heart rate of a person who is \(a\) years old.
Along with variables, and expressions, mathematical equations and inequalities are very important in algebra. In this section, we'll focus on expressions, and the remainder of this chapter is devoted to equations and inequalities.
Subsection2.1.1Introduction to Variables
When we want to represent an unknown or changing numerical quantity, we use a variable to do so. For example, if you'd like to analyze the gas mileage of various cars, you could let the symbol “\(g\)” represent a car's gas mileage. The mileage might be 25 mpg, 30 mpg, or some other quantity. If we agree to use mpg for the units of measure, \(g\) might be a place holder for \(25\text{,}\) \(30\text{,}\) or some other number. Since we are using a variable and not a specific number, we can analyze gas mileage for Honda Civics at the same time we analyze gas mileage for Ford Explorers.
When using variables to stand for actual physical quantities, it's good practice to use letters that clearly correspond to the quantity they represent. For example, it's wise to use \(g\) to represent gas mileage. This helps the people who might read your work in the future to understand it better.
At the same time you identify what variable you would like to use, it is very important to identify what units of measurement will go along with that variable, and clearly tell your reader this. For example, suppose you are working with \(g=25\text{.}\) A car whose gas mileage is 25 mpg is very different from a car whose gas mileage is 25 kpg (kilometer per gallon). So it would be important to state that \(g\) represents gas mileage in miles per gallon.
Checkpoint2.1.3
Remark2.1.4
Note that unless an algebra problem specifies which letter(s) to use, we have a choice as to which letter we choose to represent our variable(s). However without any context to a problem, \(x\text{,}\) \(y\text{,}\) and \(z\) are the most common letters used as variables, and you may see these variables (especially \(x\)) a lot.
Also note that the units we use are often determined indirectly by other quantitative information given in an algebra problem. For example, if we're told that a car has used so many gallons of gas after traveling so many miles, then it suggests we should measure gas mileage in mpg.
Subsection2.1.2Mathematical Expressions
A mathematical expression is any combination of variables and numbers using arithmetic operations. The following are all examples of mathematical expressions:
\begin{equation*}
x+1\qquad 2\ell+2w\qquad\frac{\sqrt{x}}{y+1}\qquad nRT
\end{equation*}
Note that this definition of “mathematical expression” does not include anything with signs like these in them: \(=\text{,}\) \(\lt\text{,}\) \(\leq\text{,}\) etc.
Example2.1.5
The expression:
\begin{equation*}
\frac{5}{9}(F - 32)
\end{equation*}
can be used to convert from degrees Fahrenheit to degrees Celsius. To do this, we need a Fahrenheit temperature, \(F\text{.}\) Then we can evaluate the expression. This means replacing its variable(s) with specific numbers and calculating the result. In this case, we can replace \(F\) with a specific number.
Let's convert the temperature 89 °F to the Celsius scale by evaluating the expression.
\begin{align*}
\frac{5}{9}(F - 32) \amp= \frac{5}{9}(\substitute{89} - 32)\\
\amp= \frac{5}{9}(57)\\
\amp= \frac{285}{9}\approx 31.67
\end{align*}
This shows us that 89 °F is equivalent to approximately 31.67 °C.
Warning2.1.6Vocabulary Usage
The steps in Example 2.1.5 are not considered to be “solving an equation,” which is language you might be tempted to use. Instead, this process was “evaluating an expression.” There is a special algebra meaning for words like “solve” and “solution” that will come soon.
In Example 2.1.5, we did use equals signs, but that was so we could assert that one expression equals another expression, which equals another expression, and so on. In the end, this example showed us that \(\frac{5}{9}(F - 32)\) evaluates to \(\approx31.67\) when \(F\) is \(89\text{.}\) It did not “solve” anything in a technical mathematical sense.
Checkpoint2.1.7
Try evaluating the temperature expression for yourself.
Example2.1.8Target heart rate
According to the American Heart Association, maximum heart rate in beats per minute (bpm) is given by \(220 - a\text{,}\) where \(a\) is age in years.
Determine the maximum heart rate for someone who is \(31\) years old.
Target heart rate for moderate exercise is \(50\%\) to \(70\%\) of maximum heart rate. If we want to reach \(65\%\) of an individual's maximum heart rate during moderate exercise, we'd use the expression \(0.65(220-a)\text{,}\) where \(a\) is their age in years. Determine the target heart rate at this \(65\%\) level for someone who is \(31\) years old.
Solution
Both of these parts ask us to evaluate an expression.
-
Since \(a\) is defined to be age in years, we will evaluate this expression by substituting \(a\) with \(31\text{:}\)
\begin{align*} 220-a \amp= 220-\substitute{31}\\ \amp= 189 \end{align*}This tells us that the maximum heart rate for someone who is \(31\) years old is \(189\) bpm.
-
We'll again substitute \(a\) with \(31\text{,}\) but this time using the target heart rate expression:
\begin{align*} 0.65(220-a) \amp= 0.65(220-\substitute{31})\\ \amp= 0.65(189)\\ \amp=122.85 \end{align*}This tells us that the target heart rate for someone who is \(31\) years old undertaking moderate exercise is \(122.85\) bpm.
Checkpoint2.1.9
Example2.1.10Geometry
An expression for the area of a trapezoid (shown in Figure 2.1.11) is \(\frac{1}{2}(a+b)h\text{,}\) where \(a\) and \(b\) are the parallel side lengths and \(h\) is the height. This expression is valid if \(a\text{,}\) \(b\text{,}\) and \(h\) are all measured in centimeters, inches, or any other unit for length. The result will be measured in square units, such as cm2 or in2.
Determine the area of a trapezoid for which \(a=3\,\text{cm}\text{,}\) \(b=5\,\text{cm}\text{,}\) and \(h=2\,\text{cm}\text{.}\)
Solution
Replacing each variable with the given value:
\begin{align*}
\frac{1}{2}(a+b)h \amp= \frac{1}{2}(\substitute{3\text{ cm}}+\substitute{5\text{ cm}})(\substitute{2\text{ cm}})\\
\amp= \frac{1}{2}(8\text{ cm})(2\text{ cm})\\
\amp=8\text{ cm}^2
\end{align*}
The area of this trapezoid is 8 cm2.
Checkpoint2.1.12Rising Rents
Subsection2.1.3Evaluating Expressions with Exponents, Absolute Value, and Radicals
Mathematical expressions will often have exponents, absolute value bars, and radicals. This does not change the basic approach to evaluating them.
Example2.1.13Cylinder Volume
The volume \(V\text{,}\) in cm3, of a cylinder with height \(h\) and radius \(r\text{,}\) both in cm, is given by \(V=\pi r^2h\text{.}\) Assume that a can of tuna has a radius of 4 cm and a height of 2 cm.
Calculate the volume of this can in terms of \(\pi\text{.}\)
Calculate the volume of this can and round the answer to four significant digits. Use the \(\pi\) button on your calculator, or use \(\pi\approx3.1415927\text{.}\)
Solution
-
Substitute \(r=4\) and \(h=2\) into the expression \(\pi r^2h\text{,}\) we have:
\begin{align*} V=\pi r^2h\amp=\pi(\substitute{4\text{ cm}})^2(\substitute{2\text{ cm}})\\ \amp=\pi (16\text{ cm}^2)(2\text{ cm})\\ \amp=\pi(32\text{ cm}^3)\\ \amp=32\pi\text{ cm}^3 \end{align*}The volume of this can is 32\(\pi\) cm3.
-
For this part, we substitute \(\pi\approx3.1415927\) into out first result, \(32\pi\text{,}\) and we have:
\begin{align*} V=32\pi\amp\approx 32(\substitute{3.1415927})\\ \amp\approx 100.5309\ldots\\ \amp\approx\overbrace{100.5}^{\text{four}}309\ldots \end{align*}The volume of this can is about 100.5 cm3.
Example2.1.14Tsunami Speed
The speed of a tsunami (in meters per second) can be modeled by \(\sqrt{9.8d}\text{,}\) where \(d\) is the depth of the tsunami (in meters). Determine the speed of a tsunami that has a depth of 30 m to four significant digits.
Solution
Using \(d=30\text{,}\) we find:
\begin{align*}
\sqrt{9.8d} \amp= \sqrt{9.8(\substitute{30})}\\
\amp=\sqrt{294}\\
\amp\approx \overbrace{17.14}^{\text{four}}6428\ldots
\end{align*}
The speed of tsunami with a depth of 30 m is about 17.15 m⁄s.
Checkpoint2.1.15Tent Height
Checkpoint2.1.16Mortgage Payments
Subsection2.1.4Evaluating Expressions with Negative Numbers
When we substitute negative numbers into an expression, it's important to use parentheses around them. Let's look at some examples.
Example2.1.17
Evaluate \(x^2\) if \(x=-2\text{.}\)
We substitute:
\begin{align*}
x^2\amp=(\substitute{-2})^2\\
\amp=4
\end{align*}
If we don't use parentheses, we would have:
\begin{align*}
x^2\amp=-2^2\amp\text{incorrect!}\\
\amp=-4
\end{align*}
The original expression takes \(x\) and squares it. With \(-2^2=-4\text{,}\) the number \(-2\) is not being squared. Since the exponent has higher priority than the negation, it's just the number \(2\) that is being squared. With \((-2)^2=4\) the number \(-2\) is being squared, which is what we would want given the expression \(x^2\text{.}\)
So it is wise to always use some parentheses when substituting in any negative number.
Checkpoint2.1.18
SubsectionExercises
Evaluating Expressions
1
Evaluate \({x-1}\) for \(x = 7\text{.}\)
2
Evaluate \({x-9}\) for \(x = 10\text{.}\)
3
Evaluate \({5-x}\) for \(x = -9\text{.}\)
4
Evaluate \({-2-x}\) for \(x = -7\text{.}\)
5
Evaluate \({-10x-3}\) for \(x = -4\text{.}\)
6
Evaluate \({4x+9}\) for \(x = -2\text{.}\)
7
Evaluate \({5A}\) for \(A = -3\text{.}\)
8
Evaluate \({8B}\) for \(B = -10\text{.}\)
9
Evaluate \({-9\!\left(r+3\right)}\) for \(r = 3\text{.}\)
10
Evaluate \({-4\!\left(t+10\right)}\) for \(t = -4\text{.}\)
11
Evaluate \({-7C-4a}\) for \(C = 4\) and \(a = 2\text{.}\)
12
Evaluate \({-6a+7A}\) for \(a = -1\) and \(A = -2\text{.}\)
13
Evaluate \(\displaystyle{{\frac{-3}{r}-\frac{3}{b}}}\) for \(r = 8\) and \(b = -2\text{.}\)
14
Evaluate \(\displaystyle{{\frac{-4}{a}-\frac{4}{C}}}\) for \(a = 9\) and \(C = -3\text{.}\)
15
Evaluate \(\displaystyle{{\frac{8y-5}{6y}}}\) for \(y=1\text{.}\)
16
Evaluate \(\displaystyle{{\frac{2r-8}{6r}}}\) for \(r=-6\text{.}\)
17
Evaluate \(\displaystyle{{\frac{B+5C-10}{7B+10C}}}\) for \(B=1\) and \(C=-10\text{.}\)
18
Evaluate \(\displaystyle{{\frac{-6m-8A-5}{-5m-5A}}}\) for \(m=9\) and \(A=5\text{.}\)
19
Evaluate the expression \({t^{2}}\text{:}\)
When \(t=3\text{,}\) \(\displaystyle{{t^{2}}=}\)
When \(t=-4\text{,}\) \(\displaystyle{{t^{2}}=}\)
20
Evaluate the expression \({t^{2}}\text{:}\)
When \(t=8\text{,}\) \(\displaystyle{{t^{2}}=}\)
When \(t=-8\text{,}\) \(\displaystyle{{t^{2}}=}\)
21
Evaluate the expression \({x^{3}}\text{:}\)
When \(x=3\text{,}\) \(\displaystyle{{x^{3}}=}\)
When \(x=-2\text{,}\) \(\displaystyle{{x^{3}}=}\)
22
Evaluate the expression \({x^{3}}\text{:}\)
When \(x=2\text{,}\) \(\displaystyle{{x^{3}}=}\)
When \(x=-4\text{,}\) \(\displaystyle{{x^{3}}=}\)
23
Evaluate the following expressions.
Evaluate \({5y^{2}}\) when \(y=2\text{.}\) \(\displaystyle{{5y^{2}}=}\)
Evaluate \({\left(5y\right)^{2}}\) when \(y=2\text{.}\) \(\displaystyle{{\left(5y\right)^{2}}=}\)
24
Evaluate the following expressions.
Evaluate \({3y^{2}}\) when \(y=2\text{.}\) \(\displaystyle{{3y^{2}}=}\)
Evaluate \({\left(3y\right)^{2}}\) when \(y=2\text{.}\) \(\displaystyle{{\left(3y\right)^{2}}=}\)
25
Evaluate the following expressions.
Evaluate \({r^{2}x^{3}}\) when \(r=-3\) and \(x=-1\text{.}\) \(\displaystyle{{r^{2}x^{3}}=}\)
Evaluate \({r^{3}x^{2}}\) when \(r=-3\) and \(x=-1\text{.}\) \(\displaystyle{{r^{3}x^{2}}=}\)
26
Evaluate the following expressions.
Evaluate \({r^{2}y^{3}}\) when \(r=-1\) and \(y=-4\text{.}\) \(\displaystyle{{r^{2}y^{3}}=}\)
Evaluate \({r^{3}y^{2}}\) when \(r=-1\) and \(y=-4\text{.}\) \(\displaystyle{{r^{3}y^{2}}=}\)
27
Evaluate the following expressions.
-
Evaluate \({\left(-r\right)^{2}}\) when \(r=-2\text{.}\)
\(\displaystyle{{\left(-r\right)^{2}}=}\)
-
Evaluate \({\left(-r\right)^{3}}\) when \(r=-2\text{.}\)
\(\displaystyle{{\left(-r\right)^{3}}=}\)
28
Evaluate the following expressions.
-
Evaluate \({\left(-2t\right)^{2}}\) when \(t=-1\text{.}\)
\(\displaystyle{{\left(-2t\right)^{2}}=}\)
-
Evaluate \({\left(-2t\right)^{3}}\) when \(t=-1\text{.}\)
\(\displaystyle{{\left(-2t\right)^{3}}=}\)
29
Evaluate the following expressions.
-
Evaluate \({-4t^{2}r}\) when \(t=-2\) and \(r=-1\text{.}\)
\(\displaystyle{{-4t^{2}r}=}\)
-
Evaluate \({\left(-4t\right)^{2}r}\) when \(t=-2\) and \(r=-1\text{.}\)
\(\displaystyle{{\left(-4t\right)^{2}r}=}\)
30
Evaluate the following expressions.
-
Evaluate \({-2x^{2}y}\) when \(x=-1\) and \(y=-5\text{.}\)
\(\displaystyle{{-2x^{2}y}=}\)
-
Evaluate \({\left(-2x\right)^{2}y}\) when \(x=-1\) and \(y=-5\text{.}\)
\(\displaystyle{{\left(-2x\right)^{2}y}=}\)
31
Evaluate each of the following expressions if \(x=4,\) \(y=4,\) \(z=-4.\)
\(x+12=\)
\(x+3y+z=\)
\((x-12)+3(y+z)=\)
\(100x+yz=\)
32
Evaluate each of the following expressions if \(x=4,\) \(y=7,\) \(z=-6.\)
\(x+12=\)
\(x+3y+z=\)
\((x-12)+3(y+z)=\)
\(100x+yz=\)
33
Evaluate the expression \(\displaystyle \frac{1}{7} \big( x + 2 \big)^2 - 4\) when \(x = -9\text{.}\)
34
Evaluate the expression \(\displaystyle \frac{1}{3} \big( x + 3 \big)^2 - 9\) when \(x = -6\text{.}\)
35
Evaluate the expression \(\displaystyle \frac{1}{2} h \big( B + b \big)\) when \(h = 10, \ B = 6, \ b = 3.\)
36
Evaluate the expression \(\displaystyle \frac{1}{2} h \big( B + b \big)\) when \(h = 10, \ B = 4, \ b = 5.\)
37
Evaluate the expression \(-16t^{2}+64t+128\) when \(t=5\text{.}\)
38
Evaluate the expression \(-16t^{2}+64t+128\) when \(t=4\text{.}\)
39
Evaluate each algebraic expression for the given value(s):
\(\displaystyle\frac{y^3 + \sqrt{x-2}}{|2 x - y|}\text{,}\) for \(x = 51\) and \(y = 7\text{:}\)
40
Evaluate each algebraic expression for the given value(s):
\(\displaystyle\frac{y^3 + \sqrt{x-2}}{|5 x - y|}\text{,}\) for \(x = 11\) and \(y = -3\text{:}\)
41
Evaluate each algebraic expression for the given value(s):
\(\displaystyle\frac{\sqrt{x}}{y}-\frac{y}{x}\text{,}\) for \(x = 16\) and \(y = 6\text{:}\)
42
Evaluate each algebraic expression for the given value(s):
\(\displaystyle\frac{y}{3 x} - \frac{\sqrt{x}}{2 y}\text{,}\) for \(x = 4\) and \(y = -3\text{:}\)
43
Evaluate
\begin{equation*}
\displaystyle\frac{y_2 - y_1}{x_2 - x_1}
\end{equation*}
for \(x_1 = 14\text{,}\) \(x_2 = -6\text{,}\) \(y_1 = 13\text{,}\) and \(y_2 = -13\text{:}\)
44
Evaluate
\begin{equation*}
\displaystyle\frac{y_2 - y_1}{x_2 - x_1}
\end{equation*}
for \(x_1 = 4\text{,}\) \(x_2 = -1\text{,}\) \(y_1 = 12\text{,}\) and \(y_2 = 1\text{:}\)
45
Evaluate
\begin{equation*}
\displaystyle \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\end{equation*}
for \(x_1 = -5\text{,}\) \(x_2 = -17\text{,}\) \(y_1 = -6\text{,}\) and \(y_2 = -11\text{:}\)
46
Evaluate
\begin{equation*}
\displaystyle \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\end{equation*}
for \(x_1 = 9\text{,}\) \(x_2 = 18\text{,}\) \(y_1 = -7\text{,}\) and \(y_2 = 5\text{:}\)
47
Evaluate the algebraic expression \(-7 a + b\) for \(a = {\frac{9}{5}}\) and \(b = {\frac{1}{7}}\text{.}\)
48
Evaluate the algebraic expression \(-8 a + b\) for \(a = {\frac{1}{2}}\) and \(b = {\frac{5}{3}}\text{.}\)
49
Evaluate each algebraic expression for the given value(s):
\(\displaystyle\frac{2+4|x-y|}{x+5 y}\text{,}\) for \(x = 12\) and \(y = 10\text{:}\)
50
Evaluate each algebraic expression for the given value(s):
\(\displaystyle\frac{3+3|x-y|}{x+3 y}\text{,}\) for \(x = 13\) and \(y = -13\text{:}\)
Area Formulas
51
A rectangle’s area can be calculated by the formula \(A=LW\text{,}\) where \(A\) stands for area, \(L\) for length and \(W\) for width.
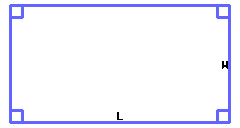
A rectangle’s perimeter can be calculated by the formula \(P=2(L+W)\text{,}\) where \(P\) stands for perimeter, \(L\) for length and \(W\) for width.
Use the formulas to calculate the rectangle’s area and perimeter. Its length is \({15\ {\rm m}}\) and its width is \({8\ {\rm m}}\text{.}\)
Area =
Perimeter =
52
A rectangle’s area can be calculated by the formula \(A=LW\text{,}\) where \(A\) stands for area, \(L\) for length and \(W\) for width.
A rectangle’s perimeter can be calculated by the formula \(P=2(L+W)\text{,}\) where \(P\) stands for perimeter, \(L\) for length and \(W\) for width.
Use the formulas to calculate the rectangle’s area and perimeter. Its length is \({15\ {\rm m}}\) and its width is \({11\ {\rm m}}\text{.}\)
Area =
Perimeter =
53
A triangle’s area can be calculated by the formula \(A=\frac{1}{2}bh\text{,}\) where \(A\) stands for area, \(b\) for base and \(h\) for height.
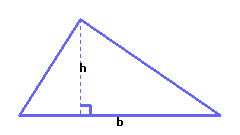
Find the triangle’s area if \(b={21\ {\rm ft}}\) and \(h={10\ {\rm ft}}\text{.}\)
Area =
54
A triangle’s area can be calculated by the formula \(A=\frac{1}{2}bh\text{,}\) where \(A\) stands for area, \(b\) for base and \(h\) for height.
Find the triangle’s area if \(b={22\ {\rm ft}}\) and \(h={8\ {\rm ft}}\text{.}\)
Area =
55
The formula
\(\displaystyle{A=\frac{1}{2}\,r\,n\,s}\)
gives the area of a regular polygon with side length \(s\text{,}\) number of sides \(n\) and, apothem \(r\text{.}\) (The apothem is the distance from the center of the polygon to one of its sides.)
What is the area of a regular pentagon with \(s= {84\ {\rm in}}\) and \(r={36\ {\rm in}}\text{?}\)
The area is .
56
The formula
\(\displaystyle{A=\frac{1}{2}\,r\,n\,s}\)
gives the area of a regular polygon with side length \(s\text{,}\) number of sides \(n\) and, apothem \(r\text{.}\) (The apothem is the distance from the center of the polygon to one of its sides.)
What is the area of a regular \(80\)-gon with \(s= {93\ {\rm in}}\) and \(r={32\ {\rm in}}\text{?}\)
The area is .
57
A trapezoid’s area can be calculated by the formula \(A=\frac{1}{2}(b_1+b_2)h\text{,}\) where \(A\) stands for area, \(b_1\) for the first base’s length, \(b_2\) for the second base’s length, and \(h\) for height.
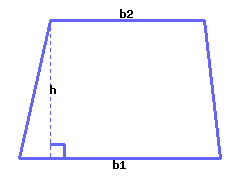
Use the formulas to calculate the trapezoid’s area. Its first base’s length is \({13\ {\rm m}}\text{,}\) its second base’s length is \({10\ {\rm m}}\) and its height is \({9\ {\rm m}}\text{.}\)
Area =
58
A trapezoid’s area can be calculated by the formula \(A=\frac{1}{2}(b_1+b_2)h\text{,}\) where \(A\) stands for area, \(b_1\) for the first base’s length, \(b_2\) for the second base’s length, and \(h\) for height.
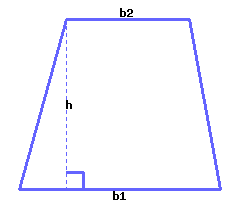
Use the formulas to calculate the trapezoid’s area. Its first base’s length is \({13\ {\rm m}}\text{,}\) its second base’s length is \({8\ {\rm m}}\) and its height is \({11\ {\rm m}}\text{.}\)
Area =
59
A circle’s circumference formula is \(C=2\pi r\text{,}\) where \(C\) stands for circumference and \(r\) for radius. And a circle’s area formula is \(A=\pi r^2\text{,}\) where \(A\) stands for area and \(r\) for radius.
Use those two formulas to answer the following questions about a circle with radius \({4\ {\rm m}}\text{.}\)
This circle’s circumference, in terms of \(\pi\text{,}\) is .
This circle’s circumference, rounded to the hundredth place, is .
This circle’s area, in terms of \(\pi\text{,}\) is .
This circle’s area, rounded to the hundredth place, is .
60
A circle’s circumference formula is \(C=2\pi r\text{,}\) where \(C\) stands for circumference and \(r\) for radius. And a circle’s area formula is \(A=\pi r^2\text{,}\) where \(A\) stands for area and \(r\) for radius.
Use those two formulas to answer the following questions about a circle with radius \({5\ {\rm m}}\text{.}\)
This circle’s circumference, in terms of \(\pi\text{,}\) is .
This circle’s circumference, rounded to the hundredth place, is .
This circle’s area, in terms of \(\pi\text{,}\) is .
This circle’s area, rounded to the hundredth place, is .
Volume Formulas
61
The formula \(V=\frac{1}{3}\cdot s^2\cdot h\) gives the volume of a right square pyramid.
What is the volume of a right square pyramid with \(s= {51\ {\rm in}}\) and \(h={58\ {\rm in}}\text{?}\)
The volume is .
62
The formula \(V=\frac{1}{3}\cdot s^2\cdot h\) gives the volume of a right square pyramid.
What is the volume of a right square pyramid with \(s= {60\ {\rm in}}\) and \(h={23\ {\rm in}}\text{?}\)
The volume is .
63
The volume of a rectangular prism can be calculated by the formula \(V=LWH\text{,}\) where \(V\) stands for volume, \(L\) for the base’s length, \(W\) for the base’s width, and \(H\) for the prism’s height.
Use the formula to calculate a rectangular prism’s volume, if its base’s length is \({14\ {\rm in}}\text{,}\) its base’s width is \({9\ {\rm in}}\text{,}\) and its height is \({13\ {\rm in}}\text{.}\)
Its volume is .
64
The volume of a rectangular prism can be calculated by the formula \(V=LWH\text{,}\) where \(V\) stands for volume, \(L\) for the base’s length, \(W\) for the base’s width, and \(H\) for the prism’s height.
Use the formula to calculate a rectangular prism’s volume, if its base’s length is \({14\ {\rm in}}\text{,}\) its base’s width is \({7\ {\rm in}}\text{,}\) and its height is \({8\ {\rm in}}\text{.}\)
Its volume is .
65
A cylinder’s volume can be calculated by the formula \(V=\pi r^2h\text{,}\) where \(V\) stands for volume, \(r\) for the base radius and \(h\) for the cylinder’s height.
Use the formula to calculate the cylinder’s volume if its base’s radius is \({6\ {\rm m}}\text{,}\) and its height is \({9\ {\rm m}}\text{.}\)
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
66
A cylinder’s volume can be calculated by the formula \(V=\pi r^2h\text{,}\) where \(V\) stands for volume, \(r\) for the base radius and \(h\) for the cylinder’s height.
Use the formula to calculate the cylinder’s volume if its base’s radius is \({5\ {\rm m}}\text{,}\) and its height is \({10\ {\rm m}}\text{.}\)
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
Evaluating Expressions in Context
67
The formula
\(\displaystyle{y=\frac{1}{2}\,a\,t^2 +v_0\,t + y_0}\)
gives the vertical position of an object, at time \(t\text{,}\) thrown with an initial velocity \(v_0\text{,}\) from an initial position \(y_0\) in a place where the acceleration of gravity is \(a\text{.}\) The acceleration of gravity on earth is \({-9.8\ {\textstyle\frac{\rm\mathstrut m}{\rm\mathstrut s^{2}}}}\text{.}\) It is negative, because we consider the upward direction as positive in this situation, and gravity pulls down.
What is the height of a baseball thrown with an initial velocity of \(v_0={57\ {\textstyle\frac{\rm\mathstrut m}{\rm\mathstrut s}}}\text{,}\) from an initial position of \(y_0= {75\ {\rm m}}\text{,}\) and at time \(t={5\ {\rm s}}\text{?}\)
Five seconds after the baseball was thrown, it was high in the air.
68
The formula
\(\displaystyle{y=\frac{1}{2}\,a\,t^2 +v_0\,t + y_0}\)
gives the vertical position of an object, at time \(t\text{,}\) thrown with an initial velocity \(v_0\text{,}\) from an initial position \(y_0\) in a place where the acceleration of gravity is \(a\text{.}\) The acceleration of gravity on earth is \({-9.8\ {\textstyle\frac{\rm\mathstrut m}{\rm\mathstrut s^{2}}}}\text{.}\) It is negative, because we consider the upward direction as positive in this situation, and gravity pulls down.
What is the height of a baseball thrown with an initial velocity of \(v_0={63\ {\textstyle\frac{\rm\mathstrut m}{\rm\mathstrut s}}}\text{,}\) from an initial position of \(y_0= {57\ {\rm m}}\text{,}\) and at time \(t={11\ {\rm s}}\text{?}\)
Eleven seconds after the baseball was thrown, it was high in the air.
69
To convert a temperature measured in degrees Fahrenheit to degrees Celsius, there is a formula:
\(\displaystyle{ C={\frac{5}{9}\!\left(F-32\right)} }\)
where \(C\) represents the temperature in degrees Celsius and \(F\) represents the temperature in degrees Fahrenheit.
If a temperature is \(50 {^\circ}\text{F}\text{,}\) what is that temperature measured in Celsius?
70
To convert a temperature measured in degrees Fahrenheit to degrees Celsius, there is a formula:
\(\displaystyle{ C={\frac{5}{9}\!\left(F-32\right)} }\)
where \(C\) represents the temperature in degrees Celsius and \(F\) represents the temperature in degrees Fahrenheit.
If a temperature is \(59 {^\circ}\text{F}\text{,}\) what is that temperature measured in Celsius?
71
A formula for converting hours into seconds is
\(\displaystyle{S = 3600H}\)
where \(H\) is a number of hours, and \(S\) is the corresponding number of seconds. Use the formula to find the number of seconds that corresponds to four hours.
seconds corresponds to four hours.
72
A formula for converting hours into seconds is
\(\displaystyle{S = 3600H}\)
where \(H\) is a number of hours, and \(S\) is the corresponding number of seconds. Use the formula to find the number of seconds that corresponds to sixteen hours.
seconds corresponds to sixteen hours.
73
The percentage of births in the U.S. delivered via C-section can be given by the following formula for the years since 1996.
\(\displaystyle{p = 0.8(y-1996)+21}\)
In this formula \(y\) is a year after 1996 and \(p\) is the percentage of births delivered via C-section for that year. What percentage of births in the U.S. were delivered via C-section in the year 2011?
of births in the U.S. were delivered via C-section in the year 2011.
74
The percentage of births in the U.S. delivered via C-section can be given by the following formula for the years since 1996.
\(\displaystyle{p = 0.8(y-1996)+21}\)
In this formula \(y\) is a year after 1996 and \(p\) is the percentage of births delivered via C-section for that year. What percentage of births in the U.S. were delivered via C-section in the year 2012?
of births in the U.S. were delivered via C-section in the year 2012.
75
Target heart rate for moderate exercise is \(50\%\) to \(70\%\) of maximum heart rate. If we want to represent a certain percent of an individual’s maximum heart rate, we’d use the formula
\(\displaystyle{\text{rate}=p(220-a)}\)
where \(p\) is the percent, and \(a\) is age in years. Determine the target heart rate at \(51\%\) level for someone who is \(53\) years old. Round your answer to an integer.
The target heart rate at \(51\%\) level for someone who is \(53\) years old is beats per minute.
76
Target heart rate for moderate exercise is \(50\%\) to \(70\%\) of maximum heart rate. If we want to represent a certain percent of an individual’s maximum heart rate, we’d use the formula
\(\displaystyle{\text{rate}=p(220-a)}\)
where \(p\) is the percent, and \(a\) is age in years. Determine the target heart rate at \(53\%\) level for someone who is \(32\) years old. Round your answer to an integer.
The target heart rate at \(53\%\) level for someone who is \(32\) years old is beats per minute.
77
The diagonal length (\(D\)) of a rectangle with side lengths \(L\) and \(W\) is given by:
\(\displaystyle{ D=\sqrt{L^2+W^2} }\)
Determine the diagonal length of rectangles with \(L={12\ {\rm ft}}\) and \(W={9\ {\rm ft}}\text{.}\)
The diagonal length of rectangles with \(L={12\ {\rm ft}}\) and \(W={9\ {\rm ft}}\) is .
78
The diagonal length (\(D\)) of a rectangle with side lengths \(L\) and \(W\) is given by:
\(\displaystyle{ D=\sqrt{L^2+W^2} }\)
Determine the diagonal length of rectangles with \(L={9\ {\rm ft}}\) and \(W={12\ {\rm ft}}\text{.}\)
The diagonal length of rectangles with \(L={9\ {\rm ft}}\) and \(W={12\ {\rm ft}}\) is .
79
The height inside a camping tent when you are \(d\) feet from the edge of the tent is given by
\(\displaystyle{h={-1.8\!\left|d-5.4\right|+6}}\)
where \(h\) stands for height in feet. Determine the height when you are:
-
\({7.1\ {\rm ft}}\) from the edge.
The height inside a camping tent when you \({7.1\ {\rm ft}}\) from the edge of the tent is
-
\({3.5\ {\rm ft}}\) from the edge.
The height inside a camping tent when you \({3.5\ {\rm ft}}\) from the edge of the tent is
80
The height inside a camping tent when you are \(d\) feet from the edge of the tent is given by
\(\displaystyle{h={-1.3\!\left|d-5.8\right|+6}}\)
where \(h\) stands for height in feet. Determine the height when you are:
-
\({10.4\ {\rm ft}}\) from the edge.
The height inside a camping tent when you \({10.4\ {\rm ft}}\) from the edge of the tent is
-
\({2\ {\rm ft}}\) from the edge.
The height inside a camping tent when you \({2\ {\rm ft}}\) from the edge of the tent is