Section1.7Notation for Intervals
¶If you say
\begin{equation*}
(\text{age of a voter})\geq18
\end{equation*}
and have a particular voter in mind, what is that person's age? There's no way to know for sure. Maybe they are \(18\text{,}\) but maybe they are older. It's helpful to visualize the possibilities with a number line, as in Figure 1.7.1.
The shaded portion of the number line in Figure 1.7.1 is a mathematical interval. For now, that just means a collection of certain numbers. In this case, it's all the numbers \(18\) and above.
It's one thing to say \((\text{age of a voter})\geq18\text{,}\) and another thing to discuss all the shaded numbers in the interval in Figure 1.7.1. In mathematics,
\begin{equation*}
(\text{age of a voter})\geq18
\end{equation*}
is saying that there is one age under consideration and all we know is that it's 18 or larger. It's subtle, but this is not the same thing as the collection of all numbers that are \(18\) or larger. Mathematics has two common ways to write down these kinds of collections.
Definition1.7.2Set-Builder Notation
Set-builder notation attempts to directly say the condition that numbers in the interval satisfy. In general, write set-builder notation like:
\begin{equation*}
\left\{x\mid\text{condition on }x\right\}
\end{equation*}
and read it out loud as “the set of all \(x\) such that ….” For example,
\begin{equation*}
\left\{x\mid x\geq18\right\}
\end{equation*}
is read out loud as “the set of all \(x\) such that \(x\) is greater than or equal to \(18\text{.}\)” The breakdown is as follows.
| \(\highlight{\{}\lowlight{x\mid x\geq18}\highlight{\}}\) | the set of |
| \(\lowlight{\{}\highlight{x}\lowlight{{}\mid x\geq18\}}\) | all \(x\) |
| \(\lowlight{\{x}\highlight{{}\mid{}}\lowlight{x\geq18\}}\) | such that |
| \(\lowlight{\{x\mid{}}\highlight{x\geq18}\lowlight{\}}\) | \(x\) is greater than or equal to \(18\) |
Definition1.7.3Interval Notation
Interval notation tries to just say the numbers where the interval starts and stops. For example, in Figure 1.7.1, the interval starts at \(18\text{.}\) To the right, the interval extends forever and has no end, so we use the \(\infty\) symbol (meaning "infinity"). This particular interval is denoted:
\begin{equation*}
[18,\infty)
\end{equation*}
Why use “\([\)” on one side and “\()\)” on the other? The square bracket tells us that \(18\) is part of the interval and the round parenthesis tells us that \(\infty\) is not part of the interval. 1 And how could it be, since \(\infty\) is not even a number?
In general there are four types of infinite intervals. Take note of the different uses of round parentheses and square brackets.
Checkpoint1.7.8Interval and Set-Builder Notation from Number Lines
SubsectionExercises
1
For each interval expressed in the number lines, give the interval notation and set-builder notation.
-
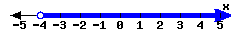
In set-builder notation:
In interval notation:
-
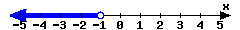
In set-builder notation:
In interval notation:
-
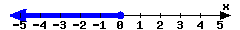
In set-builder notation:
In interval notation:
2
For each interval expressed in the number lines, give the interval notation and set-builder notation.
-
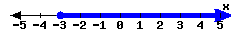
In set-builder notation:
In interval notation:
-
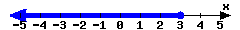
In set-builder notation:
In interval notation:
-
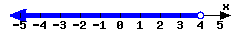
In set-builder notation:
In interval notation:
3
Here is a graph of an interval.
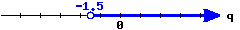
Write this inequality in set-builder notation:
Write this inequality in interval notation:
4
Here is a graph of an interval.
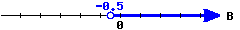
Write this inequality in set-builder notation:
Write this inequality in interval notation:
5
Here is a graph of an interval.
Write this inequality in set-builder notation:
Write this inequality in interval notation:
6
Here is a graph of an interval.
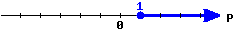
Write this inequality in set-builder notation:
Write this inequality in interval notation:
7
Here is a graph of an interval.
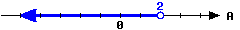
Write this inequality in set-builder notation:
Write this inequality in interval notation:
8
Here is a graph of an interval.
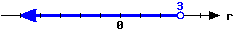
Write this inequality in set-builder notation:
Write this inequality in interval notation:
9
Here is a graph of an interval.
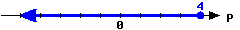
Write this inequality in set-builder notation:
Write this inequality in interval notation:
10
Here is a graph of an interval.
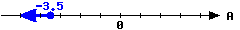
Write this inequality in set-builder notation:
Write this inequality in interval notation:
Convert set-builder notation to interval notation.
11
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {{x}} \leq -6 \} }\)
The interval notation is .
12
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {{x}} \leq -4 \} }\)
The interval notation is .
13
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {{x}} \geq -2 \} }\)
The interval notation is .
14
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {{x}} \geq 1 \} }\)
The interval notation is .
15
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid{{x}} \lt 3 \} }\)
The interval notation is .
16
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid{{x}} \lt 5 \} }\)
The interval notation is .
17
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {{x}} \gt 8 \} }\)
The interval notation is .
18
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {{x}} \gt 10 \} }\)
The interval notation is .
19
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {-9} \gt {x} \} }\)
The interval notation is .
20
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {-6} \gt {x} \} }\)
The interval notation is .
21
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {-4} \geq {x} \} }\)
The interval notation is .
22
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {-2} \geq {x} \} }\)
The interval notation is .
23
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x\mid{1} \leq {x} \} }\)
The interval notation is .
24
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x\mid{3} \leq {x} \} }\)
The interval notation is .
25
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {5} \lt {x} \} }\)
The interval notation is .
26
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {8} \lt {x} \} }\)
The interval notation is .
27
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \left\{ x \mid {{{\frac{10}{7}}}} \lt {x} \right\} }\)
The interval notation is
28
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \left\{ x \mid {{{\frac{1}{4}}}} \lt {x} \right\} }\)
The interval notation is
29
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \left\{ x \mid {{x}} \leq {-{\frac{2}{7}}} \right\} }\)
The interval notation is
30
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \left\{ x \mid {{x}} \leq {-{\frac{4}{7}}} \right\} }\)
The interval notation is
31
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid {x} \leq 0 \} }\)
The interval notation is .
32
Change the following inequality from set-builder notation to interval notation:
\(\displaystyle{ \{ x \mid 0 \lt {x} \} }\)
The interval notation is .