Skip to main content
\(\require{cancel}\newcommand{\abs}[1]{\left\lvert#1\right\rvert} \newcommand{\point}[2]{\left(#1,#2\right)} \newcommand{\highlight}[1]{{\color{blue}{{#1}}}} \newcommand{\lighthigh}[1]{{\color{magenta}{{#1}}}} \newcommand{\unhighlight}[1]{{\color{black}{{#1}}}} \newcommand{\lowlight}[1]{{\color{lightgray}{#1}}} \newcommand{\attention}[1]{\mathord{\overset{\downarrow}{#1}}} \newcommand{\substitute}[1]{{\color{blue}{{#1}}}} \newcommand{\addright}[1]{{\color{blue}{{{}+#1}}}} \newcommand{\addleft}[1]{{\color{blue}{{#1+{}}}}} \newcommand{\subtractright}[1]{{\color{blue}{{{}-#1}}}} \newcommand{\multiplyright}[2][\cdot]{{\color{blue}{{{}#1#2}}}} \newcommand{\multiplyleft}[2][\cdot]{{\color{blue}{{#2#1{}}}}} \newcommand{\divideunder}[2]{\frac{#1}{{\color{blue}{{#2}}}}} \newcommand{\divideright}[1]{{\color{blue}{{{}\div#1}}}} \newcommand{\cancelhighlight}[1]{{\color{blue}{{\cancel{#1}}}}} \newcommand{\apple}{\text{🍎}} \newcommand{\banana}{\text{🍌}} \newcommand{\pear}{\text{🍐}} \newcommand{\cat}{\text{🐱}} \newcommand{\dog}{\text{🐶}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Section1.8Chapter Review

Subsection1.8.1Review of Arithmetic with Negative Numbers

Adding Real Numbers with the Same Sign

When adding two numbers with the same sign, we can ignore the signs, and simply add the numbers as if they were both positive.

Examples

  1. \(5+2=7\)

  2. \(-5+(-2)=-7\)

Adding Real Numbers with Opposite Signs

When adding two numbers with opposite signs, we find those two numbers' difference. The sum has the same sign as the number with the bigger value. If those two numbers have the same value, the sum is \(0\text{.}\)

Examples

  1. \(5+(-2)=3\)

  2. \((-5)+2=-3\)

Subtracting a Positive Number

When subtracting a positive number, we can change the problem to adding the opposite number, and then apply the methods of adding numbers.

Examples
  1. \begin{align*} 5-2\amp=5+(-2)\\ \amp=3 \end{align*}
  2. \begin{align*} 2-5\amp=2+(-5)\\ \amp=-3 \end{align*}
  3. \begin{align*} -5-2\amp=-5+(-2)\\ \amp=-7 \end{align*}
Subtracting a Negative Number

When subtracting a negative number, we can change those two negative signs to a positive sign, and then apply the methods of adding numbers.

Examples
  1. \begin{align*} 5-(-2)\amp=5+2\\ \amp=7 \end{align*}
  2. \begin{align*} -5-(-2)\amp=-5+2\\ \amp=-3 \end{align*}
  3. \begin{align*} -2-(-5)\amp=-2+5\\ \amp=3 \end{align*}
Multiplication and Division of Real Numbers

When multiplying and dividing real numbers, each pair of negative signs cancel out each other (becoming a positive sign). If there is still one negative sign left, the result is negative; otherwise the result is positive.

Examples

  1. \((6)(-2)=-12\)

  2. \((-6)(2)=-12\)

  3. \((-6)(-2)=12\)

  4. \((-6)(-2)(-1)=-12\)

  5. \((-6)(-2)(-1)(-1)=12\)

  6. \(\frac{12}{-2}=-6\)

  7. \(\frac{-12}{2}=-6\)

  8. \(\frac{-12}{-2}=6\)

Powers

When we raise a negative number to a certain power, apply the rules of multiplying real numbers: each pair of negative signs cancel out each other.

Examples
  1. \begin{align*} (-2)^2\amp=(-2)(-2)\\ \amp=4 \end{align*}
  2. \begin{align*} (-2)^3\amp=(-2)(-2)(-2)\\ \amp=-8 \end{align*}
  3. \begin{align*} (-2)^4\amp=(-2)(-2)(-2)(-2)\\ \amp=16 \end{align*}
Difference between \((-a)^n\) and \(-a^n\)

For the exponent expression \(2^3\text{,}\) the number \(2\) is called the base, and the number \(3\) is called the exponent. The base of \((-a)^n\) is \(-a\text{,}\) while the base of \(-a^n\) is \(a\text{.}\) This makes a difference in the result when the power is an even number.

Examples
  1. \begin{align*} (-4)^2\amp=(-4)(-4)\\ \amp=16 \end{align*}
  2. \begin{align*} -4^2\amp=-(4)(4)\\ \amp=-16 \end{align*}
  3. \begin{align*} (-4)^3\amp=(-4)(-4)(-4)\\ \amp=-64 \end{align*}
  4. \begin{align*} -4^3\amp=-(4)(4)(4)\\ \amp=-64 \end{align*}

Subsection1.8.2Fraction Arithmetic Review

Multiplying Fractions

When multiplying two fractions, we simply multiply their numerators and denominators. To avoid big numbers, we should reduce fractions before multiplying. If one number is an integer, we can change the integer to a fraction with a denominator of \(1\text{.}\) For example, \(2=\frac{2}{1}\text{.}\)

\begin{align*} \frac{1}{2}\cdot\frac{3}{4}\amp=\frac{1\cdot3}{2\cdot4}\\ \amp=\frac{3}{8} \end{align*}
Dividing Fractions

When dividing two fractions, we “flip” the second number, and then do multiplication.

\begin{align*} \frac{1}{2}\div\frac{4}{3}\amp=\frac{1}{2}\cdot\frac{3}{4}\\ \amp=\frac{3}{8} \end{align*}
Adding/Subtracting Fractions

Before adding/subtracting fractions, we need to change each fraction's denominator to the same number, called the common denominator. Then, we add/subtract the numerators, and the denominator remains the same.

\begin{align*} \frac{1}{2}-\frac{1}{3}\amp=\frac{1\highlight{\cdot3}}{2\highlight{\cdot3}}-\frac{1\highlight{\cdot2}}{3\highlight{\cdot2}}\\ \amp=\frac{3}{6}-\frac{2}{6}\\ \amp=\frac{1}{6} \end{align*}

Subsection1.8.3Absolute Value and Square Root Review

Absolute Value

The absolute value of a number is the distance from that number to \(0\) on the number line. An absolute value is always positive or \(0\text{.}\)

  1. \(\abs{2}=2\)

  2. \(\abs{-\frac{1}{2}}=\frac{1}{2}\)

  3. \(\abs{0}=0\)

Square Root

The symbol \(\sqrt{b}\) has meaning when \(b\geq0\text{.}\) It means the positive number that can be squared to result in \(b\text{.}\)

  1. \(\sqrt{9}=3\)

  2. \(\sqrt{2}=1.414\ldots\)

  3. \(\sqrt{\frac{9}{16}}=\frac{3}{4}\)

  4. \(\sqrt{-1}\text{ is undefined}\)

Subsection1.8.4Order of Operations Review

Order of Operations

When evaluating an expression with multiple operations, we must follow the order of operations:

  1. (P)arentheses and other grouping symbols

  2. (E)xponentiation

  3. (M)ultiplication, (D)ivision, and Negation

  4. (A)ddition and (S)ubtraction

\begin{align*} 4-2\left( 3-(2-4)^2 \right)\amp=4-2\left( 3-(\overbrace{2-4})^2 \right)\\ \amp=4-2\left( 3-\overbrace{(\highlight{-2})^2} \right)\\ \amp=4-2\left( \overbrace{3-\highlight{4}} \right)\\ \amp=4-\overbrace{2\left( \highlight{-1} \right)}\\ \amp=4-\highlight{(-2)}\\ \amp=6 \end{align*}

Subsection1.8.5Types of Numbers Review

Types of Numbers

Real numbers are categorized into the following sets: natural numbers, whole numbers, integers, rational numbers and irrational numbers.

Examples

Here are some examples of numbers from each set of numbers:

Natural Numbers

\(1,251,3462\)

Whole Numbers

\(0,1,42,953\)

Integers

\(-263,-10,0,1,834\)

Rational Numbers

\(\frac{1}{3},-3,1.1,0,0.\overline{73}\)

Irrational Numbers

\(\pi,e,\sqrt{2}\)

Subsection1.8.6Comparison Symbols Review

The following are symbols used to compare numbers.

Symbol Meaning Examples
\(=\)

equals

 \(13=13\qquad\) \(\frac{5}{4}=1.25\)
\(\gt\)

is greater than

 \(13\gt11\) \(\pi\gt3\)
\(\geq\)

is greater than or equal to

 \(13\geq11\) \(3\geq3\)
\(\lt\)

is less than

 \(-3\lt8\) \(\frac{1}{2}\lt\frac{2}{3}\)
\(\leq\)

is less than or equal to

 \(-3\leq8\) \(3\leq3\)
\(\neq\)

is not equal to

 \(10\neq20\) \(\frac{1}{2}\neq1.2\)
Table1.8.1Comparison Symbols

Subsection1.8.7Notation for Intervals Review

The following are some examples of set-builder notation and interval notation.

Graph Set-builder Notation Interval Notation
a number line with a mark at 1; a thick line overlays the number line everywhere to the right of 1, with an arrow pointing right; there is a left bracket at 1 \(\left\{x\mid x\ge1\right\}\) \([1,\infty)\)
a number line with a mark at 1; a thick line overlays the number line everywhere to the right of 1, with an arrow pointing right; there is a left parenthesis at 1 \(\left\{x\mid x\gt1\right\}\) \((1,\infty)\)
a number line with a mark at 1; a thick line overlays the number line everywhere to the left of 1, with an arrow pointing left; there is a right bracket at 1 \(\left\{x\mid x\le1\right\}\) \((-\infty,1]\)
a number line with a mark at 1; a thick line overlays the number line everywhere to the left of 1, with an arrow pointing left; there is a right parenthesis at 1 \(\left\{x\mid x\lt1\right\}\) \((-\infty,1)\)

SubsectionExercises

1

Perform the given addition and subtraction:

  1. \(\displaystyle{ {-14-6+\left(-3\right)}= }\)

  2. \(\displaystyle{ {5-\left(-19\right)+\left(-17\right)}= }\)

2

Multiply the following integers.

  1. \(\displaystyle{ (-1)\cdot(-6)\cdot(-5) = }\)

  2. \(\displaystyle{ 3\cdot(-9)\cdot(-1)= }\)

  3. \(\displaystyle{ (-98)\cdot(-50)\cdot0= }\)

3

Evaluate the following.

  1. \(\displaystyle{ \frac{-27}{-3}= }\)

  2. \(\displaystyle{ \frac{50}{-5}= }\)

  3. \(\displaystyle{ \frac{-25}{5}= }\)

4

Evaluate the following expressions that have integer exponents:

  1. \(\displaystyle{ (-1)^{2}= }\)

  2. \(\displaystyle{ -6^{2}= }\)

5

Evaluate the following expressions that have integer exponents:

  1. \(\displaystyle{ (-4)^{3}= }\)

  2. \(\displaystyle{ -1^{3}= }\)

6

Add these two fractions: \(\displaystyle{-\frac{1}{6} + \frac{9}{10}}\)

7

Subtract one fraction from the other: \(\displaystyle{-\frac{5}{6} - \left(-\frac{3}{10}\right)}\)

8

Carry out the subtraction: \(\displaystyle{ -1 - \frac{13}{2}}\)

9

Multiply these two fractions: \(\displaystyle{-\frac{3}{2} \cdot \frac{11}{9}}\)

10

Multiply the integer with the fraction: \(\displaystyle{-8\cdot \frac{9}{28} }\)

11

Carry out the division: \(\displaystyle{ \frac{7}{12} \div \left(-\frac{2}{15}\right) }\)

12

Carry out the division: \(\displaystyle{16 \div \frac{8}{5} }\)

13

Evaluate the following expressions which involve the absolute value:

  1. \(\displaystyle{ - \lvert 2-9 \rvert = }\)

  2. \(\displaystyle{ \lvert -2-9 \rvert = }\)

  3. \(\displaystyle{ -2 \lvert 9-2 \rvert = }\)

14

Find the square root of the following numbers:

  1. \(\displaystyle{ \sqrt{1} }\) =

  2. \(\displaystyle{ \sqrt{144} }\) =

  3. \(\displaystyle{ \sqrt{9} }\) =

15

Find the square root of the following numbers.

  1. \(\displaystyle{ \sqrt{{{\frac{9}{64}}}} }\) =

  2. \(\displaystyle{ \sqrt{{-{\frac{81}{16}}}} }\) =

16

Evaluate this expression:

\(\displaystyle{ -4^{2}-5[ 1-( 3-4^{3} ) ] = }\)

17

Evaluate this expression:

\(\displaystyle{ \frac{1-(-4)^{3}}{5-10} = }\)

18

Evaluate this expression:

\(\displaystyle{ 6-6\left\lvert -1+(4-7)^{3}\right\rvert = }\)

19

Compare the following integers:

\(-3\)

  • <

  • >

  • =

\(3\)

\(-6\)

  • <

  • >

  • =

\(-3\)

\(-3\)

  • <

  • >

  • =

\(0\)

20

Change the following inequality from set-builder notation to interval notation:

\(\displaystyle{ \{ x \mid {{x}} \gt 5 \} }\)

The interval notation is .

21

Give examples of each type of number. If no such number exists, enter DNE or NONE.

  1. Give an example of a whole number that is not an integer.

  2. Give an example of an integer that is not a whole number.

  3. Give an example of a rational number that is not an integer.

  4. Give an example of a irrational number.

  5. Give an example of a irrational number that is also an integer.

22

Here is a graph of an interval.

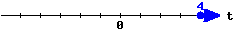
Write this inequality in set-builder notation:

Write this inequality in interval notation: