Section10.2Domain and Range
¶A function is a process for turning input values into output values. Occasionally a function \(f\) will have input values for which the process breaks down.
Subsection10.2.1Domain
Example10.2.2
Let \(P\) be the population of Portland as a function of the year. According to Google 1 https://www.google.com/publicdata/explore?ds=kf7tgg1uo9ude_&met_y=population&hl=en&dl=en#!ctype=l&strail=false &bcs=d&nselm=h&met_y=population&scale_y=lin&ind_y=false&rdim=country&idim=place:4159000&ifdim=country &hl=en_US&dl=en&ind=false we can say that:
But what if we asked to find \(P(1600)\text{?}\) The question doesn't really make sense anymore. The Multnomah tribe lived in villages in the area, but the city of Portland was not incorporated until 1851. We say that \(P(1600)\) is undefined.
Example10.2.3
If \(m\) is a person's mass in kg, let \(w(m)\) be their weight in lb. There is an approximate formula for \(w\text{:}\)
From this formula we can find:
which tells us that a \(50\)-kg person weighs 110 lb, and an \(80\)-kg person weighs 176 lb.
What if we asked for \(w(-100)\text{?}\) In the context of this example, we would be asking for the weight of a person whose mass is -100 kg. This is clearly nonsense. That means that \(w(-100)\) is undefined. Note that the context of the example is telling us that \(w(-100)\) is undefined even though the formula alone might suggest that \(w(-100)=-220\text{.}\)
Example10.2.4
Let \(g\) have the formula
For most \(x\)-values, \(g(x)\) is perfectly computable:
But if we try to compute \(g(7)\text{,}\) we run into an issue of arithmetic.
The expression \(\frac{7}{0}\) is undefined. There is no number that this could equal.
Checkpoint10.2.5
These examples should motivate the following definition.
Definition10.2.6Domain
The domain of a function \(f\) is the collection of all of its valid input values.
Example10.2.7
Referring to the functions from Examples 10.2.2–10.2.4
The domain of \(P\) is all years starting from 1851 and later. It would also be reasonable to say that the domain is actually all years from 1851 up to the current year, since we cannot guarantee that Portland will exist forever.
The domain of \(w\) is all positive real numbers. It is nonsensical to have a person with negative mass or even one with zero mass. While there is some lower bound for the smallest mass a person could have, and also an upper bound for the largest mass a person could have, these boundaries are gray. We can say for sure that non-positive numbers should never be used as inputs for \(w\text{.}\)
The domain of \(g\) is all real numbers except \(7\text{.}\) This is the only number that causes a breakdown in \(g\)'s formula.
Subsection10.2.2Interval, Set, and Set-Builder Notation
Communicating the domain of a function can be wordy. In mathematics, we can communicate the same information using concise notation that is accepted for use almost everywhere. Table 10.2.8 contains example functions from this section and their domains, and demonstrates interval notation for these domains. Basic interval notation is covered in Section 1.7, but some of our examples here go beyond what that section covers.
| Function | Verbal Domain | Number Line Illustration | Interval Notation |
\(P\) from Example 10.2.2 |
all years 1851 and greater |
\([1851,\infty)\) | |
\(w\) from Example 10.2.3 |
all real numbers greater than \(0\) |
\((0,\infty)\) | |
\(g\) from Example 10.2.4 |
all real numbers except \(7\) |
\((-\infty,7)\cup(7,\infty)\) |
Again, basic interval notation is covered in Section 1.7, but one thing appears in Table 10.2.8 that is not explained in that earlier section: the \(\cup\) symbol, which we see in the domain of \(g\text{.}\)
Occasionally there is a need to consider number line pictures such as Figure 10.2.9, where two or more intervals appear.
This picture is trying to tell you to consider numbers that are between \(-5\) and \(1\text{,}\) together with numbers that are between \(4\) and \(7\text{.}\) That word “together” is related to the word “union,” and in math the union symbol, \(\cup\text{,}\) captures this idea. So we can write the numbers in this picture as
(which uses interval notation).
With the domain of \(g\) in Table 10.2.8, the number line picture shows us another “union” of two intervals. They are very close together, but there are still two separated intervals in that picture: \((-\infty,7)\) and \((7,\infty)\text{.}\) Their union is represented by \((-\infty,7)\cup(7,\infty)\text{.}\)
Checkpoint10.2.10
Checkpoint10.2.11
Sometimes we will consider collections of only a short list of numbers. In those cases, we use set notation (first introduced in Section 1.5). With set notation, we have a list of numbers in mind, and we simply list all of those numbers. Curly braces are standard for surrounding the list. Table 10.2.12 illustrates set notation in use.
| Picture of Set | Set Notation |
| \(\{-2,3\}\) | |
| \(\{-5,1,3,5\}\) | |
| \(\{-2\}\cup(5,\infty)\) |
Checkpoint10.2.13
While most collections of numbers that we will encounter can be described using a combination of interval notation and set notation, there is another commonly used notation that is very useful in algebra: set-builder notation, which was introduced in Section 1.7. Set-builder notation also uses curly braces. Set-builder notation provides a template for what a number that is under consideration might look like, and then it gives you restrictions on how to use that template. A very basic example of set-builder notation is
Verbally, this is “the set of all \(x\) such that \(x\) is greater than or equal to \(3\text{.}\)” Table 10.2.14 gives more examples of set-builder notation in use.
| Picture of Set | Set Notation |
| \(\{x\mid -2\lt x \leq3\}\) | |
| \(\{x\mid x\lt1\text{ or }x>3\}\) |
Checkpoint10.2.15
Example10.2.16
What is the domain of the function \(A\text{,}\) where \(A(x)=\frac{2x+1}{x^2-2x-8}\text{?}\)
Note that if you plugged in some value for \(x\text{,}\) the only thing that might go wrong is if the denominator equals \(0\text{.}\) So a bad value for \(x\) would be when
Here, we used a basic factoring technique from Section 7.3. To continue, either
These are the bad \(x\)-values because they lead to division by \(0\) in the formula for \(A\text{.}\) So on a number line, if we wanted to picture the domain of \(A\text{,}\) we would make a sketch like:
So the domain is the union of three intervals: \((-\infty,-2)\cup(-2,4)\cup(4,\infty)\text{.}\)
Example10.2.17
What is the domain of the function \(B\text{,}\) where \(B(x)=\sqrt{7-x}+3\text{?}\)
Note that if you plugged in some value for \(x\text{,}\) the only thing that might go wrong is if the value in the radical is negative. So the good values for \(x\) would be when
So on a number line, if we wanted to picture the domain of \(B\text{,}\) we would make a sketch like:
So the domain is the interval \((-\infty,7]\text{.}\)
There are three main properties of algebraic functions that cause numbers to be excluded from a domain, which are summarized here.
- Denominators
-
Division by zero is undefined. So if a function contains an expression in a denominator, it will only be defined where that expression is not equal to zero.
Example 10.2.16 demonstrates this.
- Square Roots
-
The square root of a negative number is undefined. So if a function contains a square root, it will only be defined when the expression inside that radical is greater than or equal to zero. (This is actually true for any even \(n\)th radical.)
Example 10.2.17 demonstrates this.
- Context
-
Some numbers are nonsensical in context. If a function has real-world context, then this may add additional restrictions on the input values.
Example 10.2.3 demonstrates this.
Subsection10.2.3Range
The domain of a function is the collection of its valid inputs; there is a similar notion for output.
Definition10.2.19Range
The range of a function \(f\) is the collection of all of its possible output values.
Example10.2.20
Let \(f\) be the function defined by the formula \(f(x)=x^2\text{.}\) Finding \(f\)'s domain is straightforward. Any number anywhere can be squared to produce an output, so \(f\) has domain \((-\infty,\infty)\text{.}\) What is the range of \(f\text{?}\)
We would like to describe the collection of possible numbers that \(f\) can give as output. We will use a graphical approach. Figure 10.2.21 displays a graph of \(f\text{,}\) and the visualization that reveals \(f\)'s range.
Output values are the \(y\)-coordinates in a graph. If we “slide the ink” left and right over to the \(y\)-axis to emphasize what the \(y\)-values in the graph are, we have \(y\)-values that start from \(0\) and continue upward forever. Therefore the range is \([0,\infty)\text{.}\)
Warning10.2.22Finding range from a formula
Sometimes it is possible to compute a range without the aid of a graph. However, doing so can often require techniques covered in calculus. Therefore when you are asked to find the range of a function based on its formula, your approach will most often need to be a graphical one.
Example10.2.23
Given the function \(g\) graphed in Figure 10.2.24, find the domain and range of \(g\text{.}\)
To find the domain, we can visualize all of the \(x\)-values that are valid inputs for this function by “sliding the ink” down onto the \(x\)-axis. The arrows at the far left and far right of the curve indicate that whatever pattern we see in the graph continues off to the left and right. Here, we see that the arms of the graph appear to be tapering down to the \(x\)-axis and extending left and right forever. Every \(x\)-value can be used to get an output for the function, so the domain is \((-\infty,\infty)\text{.}\)
If we visualize the possible outputs by “sliding the ink” sideways onto the \(y\)-axis, we find that outputs as high as \(3\) are possible (including \(3\) itself). The outputs appear to get very close to \(0\) when \(x\) is large, but they aren't quite equal to \(0\text{.}\) So the range is \((0,3]\text{.}\)
Checkpoint10.2.27
The examples of finding domain and range so far have all involved either a verbal description of a function, a formula for that function, or a graph of that function. Recall that there is a fourth perspective on functions: a table. In the case of a table, we have very limited information about the function's inputs and outputs. If the table is all that we have, then there are a handful of input values listed in the table for which we know outputs. For any other input, the output is undefined.
Example10.2.28
Consider the function \(k\) given in Table 10.2.29. What is the domain and range of \(k\text{?}\)
| \(x\) | \(k(x)\) |
| \(3\) | \(4\) |
| \(8\) | \(5\) |
| \(10\) | \(5\) |
All that we know about \(k\) is that \(k(3)=4\text{,}\) \(k(8)=5\text{,}\) and \(k(10)=5\text{.}\) Without any other information such as a formula for \(k\) or a context for \(k\) that tells us its verbal description, we must assume that its domain is \(\{3,8,10\}\text{;}\) these are the only valid input for \(k\text{.}\) Similarly, \(k\)'s range is \(\{4,5\}\text{.}\)
Note that we have used set notation, not interval notation, since the answers here were lists of \(x\)-values (for the domain) and \(y\)-values (for the range). Also note that we could graph the information that we have about \(k\) in Figure 10.2.30, and the visualization of “sliding ink” to determine domain and range still works.
SubsectionExercises
Find domain and range using context.
1
Subin bought a used car for \({\$7{,}600}\text{.}\) The car’s value decreases at a constant rate each year. After \(10\) years, the value decreased to \({\$3{,}600}\text{.}\)
Use a function to model the car’s value as the number of years increases. Find this function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
2
Priscilla bought a used car for \({\$8{,}800}\text{.}\) The car’s value decreases at a constant rate each year. After \(7\) years, the value decreased to \({\$6{,}000}\text{.}\)
Use a function to model the car’s value as the number of years increases. Find this function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
3
Assume a car uses gas at a constant rate. After driving \(15\) miles since a full tank of gas was purchased, there was \(11.4\) gallons of gas left; after driving \(70\) miles since a full tank of gas was purchased, there was \(9.2\) gallons of gas left.
Use a function to model the amount of gas in the tank (in gallons). Let the independent variable be the number of miles driven since a full tank of gas was purchased. Find this function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
4
Assume a car uses gas at a constant rate. After driving \(10\) miles since a full tank of gas was purchased, there was \(13.5\) gallons of gas left; after driving \(60\) miles since a full tank of gas was purchased, there was \(11\) gallons of gas left.
Use a function to model the amount of gas in the tank (in gallons). Let the independent variable be the number of miles driven since a full tank of gas was purchased. Find this function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
5
Assume a tree grows at a constant rate. When the tree was planted, it was \(3.4\) feet tall. After \(8\) years, the tree grew to \(6.6\) feet tall.
Use a function to model the tree’s height as years go by. Assume the tree can live \(180\) years, find this function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
6
Assume a tree grows at a constant rate. When the tree was planted, it was \(3.6\) feet tall. After \(10\) years, the tree grew to \(11.6\) feet tall.
Use a function to model the tree’s height as years go by. Assume the tree can live \(160\) years, find this function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
7
Lily inherited a collection of coins when she was \(15\) years old. Ever since, she has been adding into the collection the same number of coins each year. When she was \(20\) years old, there were \(410\) coins in the collection. When she was \(29\) years old, there were \(680\) coins in the collection. At the age of \(55\text{,}\) Lily donated all her coins to a museum.
Use a function to model the number of coins in Lily’s collection, starting in the year she inherited the collection, and ending in the year the collection was donated. Find this function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
8
Virginia inherited a collection of coins when she was \(10\) years old. Ever since, she has been adding into the collection the same number of coins each year. When she was \(19\) years old, there were \(635\) coins in the collection. When she was \(28\) years old, there were \(1040\) coins in the collection. At the age of \(60\text{,}\) Virginia donated all her coins to a museum.
Use a function to model the number of coins in Virginia’s collection, starting in the year she inherited the collection, and ending in the year the collection was donated. Find this function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
9
An object was shot up into the air at an initial vertical speed of \(352\) feet per second. Its height as time passes can be modeled by the quadratic function \(f\text{,}\) where \(f(t)={-16t^{2}+352t}\text{.}\) Here \(t\) represents the number of seconds since the object’s release, and \(f(t)\) represents the object’s height in feet.
Find the function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
10
An object was shot up into the air at an initial vertical speed of \(384\) feet per second. Its height as time passes can be modeled by the quadratic function \(f\text{,}\) where \(f(t)={-16t^{2}+384t}\text{.}\) Here \(t\) represents the number of seconds since the object’s release, and \(f(t)\) represents the object’s height in feet.
Find the function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
11
From a clifftop over the ocean \({439.04\ {\rm m}}\) above sea level, an object was shot straight up into the air with an initial vertical speed of \({90.16\ {\textstyle\frac{\rm\mathstrut m}{\rm\mathstrut s}}}\text{.}\) On its way down it missed the cliff and fell into the ocean. Its height (above sea level) as time passes can be modeled by the quadratic function \(f\text{,}\) where \(f(t)={-4.9t^{2}+90.16t+439.04}\text{.}\) Here \(t\) represents the number of seconds since the object’s release, and \(f(t)\) represents the object’s height (above sea level) in meters.
Find the function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
12
From a clifftop over the ocean \({426.3\ {\rm m}}\) above sea level, an object was shot straight up into the air with an initial vertical speed of \({127.4\ {\textstyle\frac{\rm\mathstrut m}{\rm\mathstrut s}}}\text{.}\) On its way down it missed the cliff and fell into the ocean. Its height (above sea level) as time passes can be modeled by the quadratic function \(f\text{,}\) where \(f(t)={-4.9t^{2}+127.4t+426.3}\text{.}\) Here \(t\) represents the number of seconds since the object’s release, and \(f(t)\) represents the object’s height (above sea level) in meters.
Find the function’s domain and range in this context.
The function’s domain in this context is .
The function’s range in this context is .
13
You will build a rectangular sheep pen next to a river. There is no need to build a fence along the river, so you only need to build three sides. You have a total of \(460\) feet of fence to use. Find the dimensions of the pen such that you can enclose the maximum area.
Use a function to model the area of the rectangular pen, with respect to the length of the width (the two sides perpendicular to the river). Find the function’s domain and range in this context.
The function’s domain is .
The function’s range is .
14
You will build a rectangular sheep pen next to a river. There is no need to build a fence along the river, so you only need to build three sides. You have a total of \(470\) feet of fence to use. Find the dimensions of the pen such that you can enclose the maximum area.
Use a function to model the area of the rectangular pen, with respect to the length of the width (the two sides perpendicular to the river). Find the function’s domain and range in this context.
The function’s domain is .
The function’s range is .
Find domain and range using a graph.
15
A function’s graph is shown below.
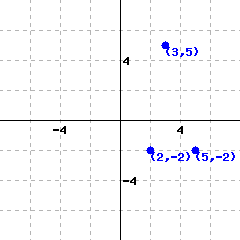
The domain of this function is .
The range of this function is .
16
A function’s graph is shown below.
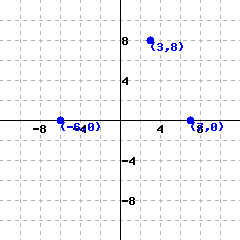
The domain of this function is .
The range of this function is .
17
A function’s graph is shown below.
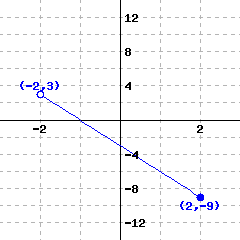
Use interval notation to answer the following questions.
The domain of this function is .
The range of this function is .
18
A function’s graph is shown below.
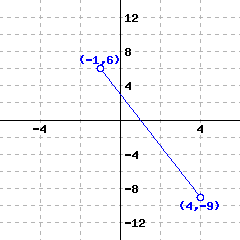
Use interval notation to answer the following questions.
The domain of this function is .
The range of this function is .
19
A function’s graph is shown below.
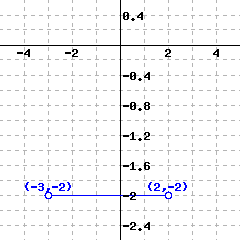
Use interval notation or set notation to answer the following questions.
The domain of this function is .
The range of this function is .
20
A function’s graph is shown below.
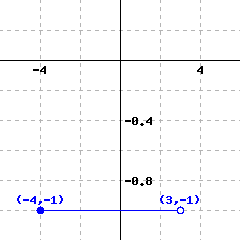
Use interval notation or set notation to answer the following questions.
The domain of this function is .
The range of this function is .
21
A function’s graph is shown below.
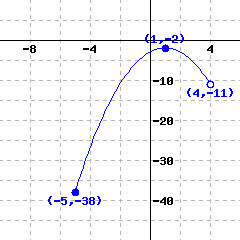
Use interval notation to answer the following questions.
The domain of this function is .
The range of this function is .
22
A function’s graph is shown below.
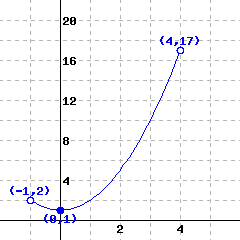
Use interval notation to answer the following questions.
The domain of this function is .
The range of this function is .
23
A function’s graph is shown below.

Note that the function has a horizontal asymptote and a vertical asymptote. Use interval notation to answer the following questions.
The domain of this function is .
The range of this function is .
24
A function’s graph is shown below.
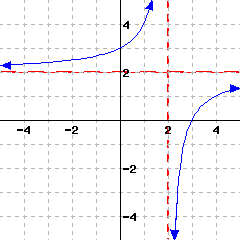
Note that the function has a horizontal asymptote and a vertical asymptote. Use interval notation to answer the following questions.
The domain of this function is .
The range of this function is .
25
A function’s graph is shown below.
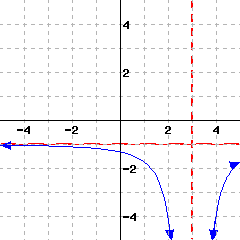
Note that the function has a horizontal asymptote and a vertical asymptote. Use interval notation to answer the following questions.
The domain of this function is .
The range of this function is .
26
A function’s graph is shown below.
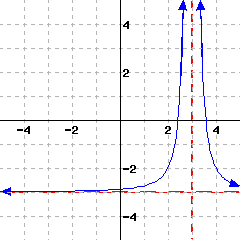
Note that the function has a horizontal asymptote and a vertical asymptote. Use interval notation to answer the following questions.
The domain of this function is .
The range of this function is .
27
Use the graph of \(f\) below to estimate its domain and range.
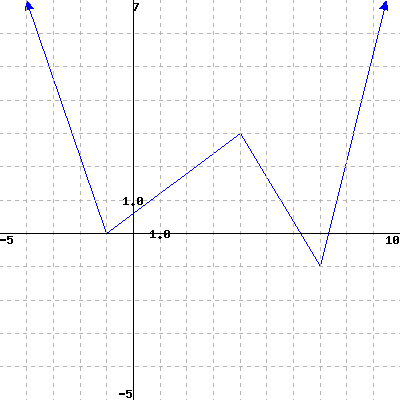
The domain is .
The range is .
28
Use the graph of \(g\) below to estimate its domain and range.
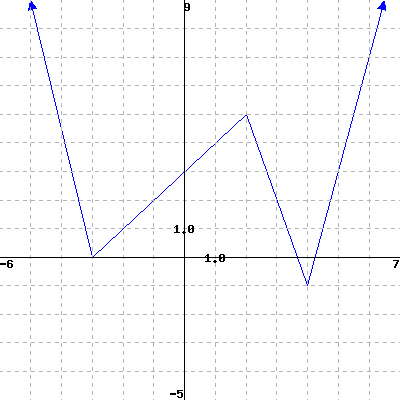
The domain is .
The range is .
29
The graph of function \(f(x)\) is shown below.
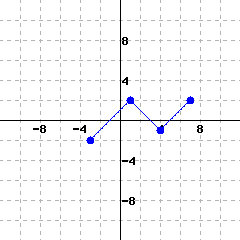
Based on the given graph of \(f(x)\text{,}\) fill in the blanks. If there are more than one answers for a blank, use a comma to separate your answers.
\(f(0)\)=
\(f(\)\()=0\)
The function’s domain, in interval notation, is .
The function’s range, in interval notation, is .
30
The graph of function \(f(x)\) is shown below.
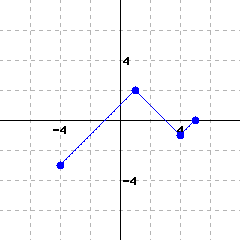
Based on the given graph of \(f(x)\text{,}\) fill in the blanks. If there are more than one answers for a blank, use a comma to separate your answers.
\(f(0)\)=
\(f(\)\()=0\)
The function’s domain, in interval notation, is .
The function’s range, in interval notation, is .
31
The graph of function \(f(x)\) is shown below.

Based on the given graph of \(f(x)\text{,}\) fill in the blanks.
\(f(-1)\)=
The function’s domain, in interval notation, is .
The function’s range, in interval notation, is .
32
The graph of function \(f(x)\) is shown below.
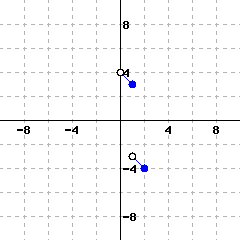
Based on the given graph of \(f(x)\text{,}\) fill in the blanks.
\(f(1)\)=
The function’s domain, in interval notation, is .
The function’s range, in interval notation, is .
33
Use the graph of \(H\) below to estimate its domain and range.
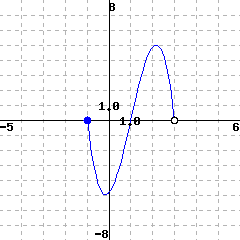
The domain is (in interval notation).
The range is (in interval notation).
34
Use the graph of \(K\) below to estimate its domain and range.
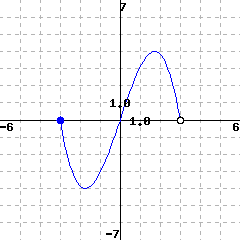
The domain is (in interval notation).
The range is (in interval notation).
35
Use the graph of \(K\) below to estimate its domain and range.
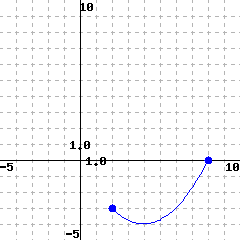
The domain is (in interval notation).
The range is (in interval notation).
36
Use the graph of \(f\) below to estimate its domain and range.
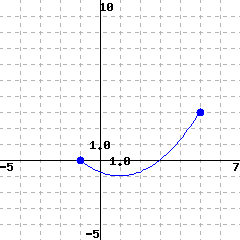
The domain is (in interval notation).
The range is (in interval notation).
37
Use the graph of \(g\) below to estimate its domain and range.
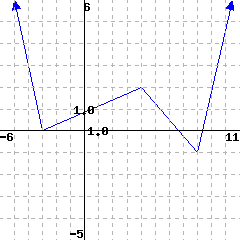
The domain is (in interval notation).
The range is (in interval notation).
38
Use the graph of \(h\) below to estimate its domain and range.
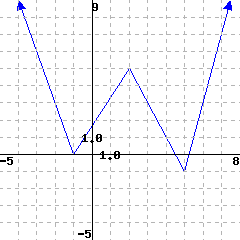
The domain is (in interval notation).
The range is (in interval notation).
39
Use the graph of \(F\) below to estimate its domain and range.
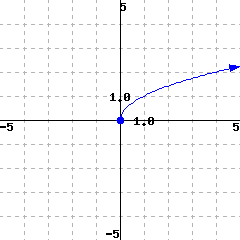
The domain is (in interval notation).
The range is (in interval notation).
40
Use the graph of \(F\) below to estimate its domain and range.
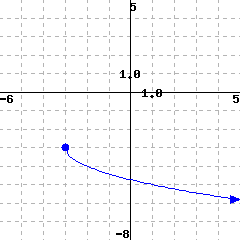
The domain is (in interval notation).
The range is (in interval notation).
41
Use the graph of \(G\) below to estimate its domain and range.
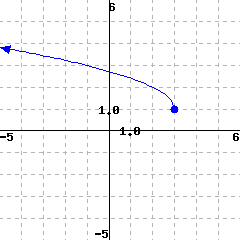
The domain is (in interval notation).
The range is (in interval notation).
42
Use the graph of \(H\) below to estimate its domain and range.

The domain is (in interval notation).
The range is (in interval notation).
Find domain using a function's formula.
43
Find the domain of \(K\) where \(K\!\left(x\right)=-8x-2\text{.}\)
The domain is (in interval notation).
44
Find the domain of \(K\) where \(K\!\left(x\right)=6x+7\text{.}\)
The domain is (in interval notation).
45
Find the domain of \(f\) where \(\displaystyle{f(x)={{\frac{5}{4}}x^{4}}}\text{.}\)
The domain is (in interval notation).
46
Find the domain of \(g\) where \(\displaystyle{g(x)={{\frac{1}{8}}x^{2}}}\text{.}\)
The domain is (in interval notation).
47
Find the domain of \(h\) where \(\displaystyle{h(x)=\lvert {5x-9} \rvert}\text{.}\)
48
Find the domain of \(F\) where \(\displaystyle{F(x)=\lvert {-3x+4} \rvert}\text{.}\)
49
Find the domain of \(\displaystyle{F}\) where \(\displaystyle{F(x)={\frac{8x}{x+10}}}\text{.}\)
The domain is (in interval notation).
50
Find the domain of \(\displaystyle{G}\) where \(\displaystyle{G(x)={\frac{3x}{x-4}}}\text{.}\)
The domain is (in interval notation).
51
Find the domain of \(\displaystyle{H}\) where \(\displaystyle{H(x)={\frac{7x}{4x+3}}}\text{.}\)
The domain is in interval notation.
52
Find the domain of \(\displaystyle{K}\) where \(\displaystyle{K(x)={\frac{2x}{7x-10}}}\text{.}\)
The domain is in interval notation.
53
Find the domain of \(\displaystyle{K}\) where \(\displaystyle{K(x)={\frac{3x+2}{x^{2}-10x+24}}}\text{.}\)
The domain is in interval notation.
54
Find the domain of \(\displaystyle{f}\) where \(\displaystyle{f(x)={-\frac{4x+10}{x^{2}-16x+60}}}\text{.}\)
The domain is in interval notation.
55
Find the domain of \(\displaystyle{g}\) where \(\displaystyle{g(x)={\frac{9x-2}{x^{2}+5x}}}\text{.}\)
The domain is in interval notation.
56
Find the domain of \(\displaystyle{h}\) where \(\displaystyle{h(x)={\frac{2x+7}{x^{2}-x}}}\text{.}\)
The domain is in interval notation.
57
Find the domain of \(\displaystyle{F}\) where \(\displaystyle{F(x)={-\frac{5x+5}{x^{2}-81}}}\text{.}\)
The domain is in interval notation.
58
Find the domain of \(\displaystyle{F}\) where \(\displaystyle{F(x)={\frac{8x+4}{x^{2}-1}}}\text{.}\)
The domain is in interval notation.
59
Find the domain of \(\displaystyle{G}\) where \(\displaystyle{G(x)={\frac{x-9}{49x^{2}-9}}}\text{.}\)
The domain is in interval notation.
60
Find the domain of \(\displaystyle{H}\) where \(\displaystyle{H(x)={-\frac{6x+3}{9x^{2}-16}}}\text{.}\)
The domain is in interval notation.
61
Find the domain of \(\displaystyle{K}\) where \(\displaystyle{K(x)={\frac{8x+9}{x^{2}+1}}}\text{.}\)
The domain is in interval notation.
62
Find the domain of \(\displaystyle{K}\) where \(\displaystyle{K(x)={\frac{6-3x}{x^{2}+2}}}\text{.}\)
The domain is in interval notation.
63
Find the domain of \(f\) where \(f(x)={-\frac{7}{\sqrt{x+5}}}\text{.}\)
64
Find the domain of \(g\) where \(g(x)={\frac{7}{\sqrt{x-7}}}\text{.}\)
65
Find the domain of \(h\) where \(h(x)={\sqrt{6-x}}\text{.}\)
66
Find the domain of \(h\) where \(h(x)={\sqrt{3-x}}\text{.}\)
67
Find the domain of \(F\) where \(F(x)={\sqrt{8+9x}}\text{.}\)
68
Find the domain of \(G\) where \(G(x)={\sqrt{5+17x}}\text{.}\)
69
Using interval notation, the domain of the function \(t\) defined by \(\displaystyle{t(x)=\frac{x+16}{x^2-4}}\)
is
70
Using interval notation, the domain of the function \(C\) defined by \(\displaystyle{C(x)=\frac{x+18}{x^2-225}}\)
is
71
Using interval notation, the domain of the function \(y\) defined by\(\displaystyle{y(x)= \frac{16x - 3}{x^2+ 7 x-98} }\)
is
72
Using interval notation, the domain of the function \(A\) defined by\(\displaystyle{A(x)= \frac{16x - 12}{x^2+ 2 x-8} }\)
is
73
Using interval notation, the domain of the function \(p\) defined by \(\displaystyle{p(x)= \frac{\sqrt{5 + x}}{7 - x}}\)
is
74
Using interval notation, the domain of the function \(a\) defined by \(\displaystyle{a(x)= \frac{\sqrt{7 + x}}{4 - x}}\)
is
75
Answer the following vocabulary questions. Each answer blank may accept several correct options as long as they mean the same thing. Whatever you answer with, correct spelling is important.
The collection of all possible output values from a function is called the of that function.
The collection of all valid input values for a function is called the of that function.
When we write \(y=f(x)\text{,}\) we call \(x\) the variable, and we call \(y\) the variable.
