ORCCA Chapter Review

Section2.9Chapter Review

Subsection2.9.1Variables and Evaluating Expressions Review

Evaluating Expressions

When we evaluate an expression's value, we substitute each variable with its given value.

Example

Evaluate the value of $\frac{5}{9}(F - 32)$ if $F=212\text{.}$

\begin{align*} \frac{5}{9}(F - 32)\amp=\frac{5}{9}(212 - 32)\\ \amp=\frac{5}{9}(180)\\ \amp=100 \end{align*}

Substituting a Negative Number

When we substitute a variable with a negative number, it's important to use parentheses around the number.

Example

Evaluate the following expressions if $x=-3\text{.}$

\begin{align*} x^2\amp=(-3)^2\\ \amp=9 \end{align*}
\begin{align*} x^3\amp=(-3)^3\\ \amp=(-3)(-3)(-3)\\ \amp=-27 \end{align*}
\begin{align*} -x^2\amp=-(-3)^2\\ \amp=-9 \end{align*}
\begin{align*} -x^3\amp=-(-3)^3\\ \amp=-(-27)\\ \amp=27 \end{align*}

Subsection2.9.2Equations and Inequalities as True/False Statements Review

Checking Possible Solutions

Given an equation or an inequality (with one variable), checking if some particular number is a solution is just a matter of replacing the value of the variable with the specified number and determining if the resulting equation/inequality is true or false. This may involve some amount of arithmetic simplification.

Example

Is $-5$ a solution to $2(x+3)-2=4-x\text{?}$

To find out, substitute in $-5$ for $x$ and see what happens.

\begin{align*} 2(x+3)-2\amp=4-x\\ 2(\substitute{(-5)}+3)-2\amp\stackrel{?}{=}4-\substitute{(-5)}\\ 2(\highlight{-2})-2\amp\stackrel{?}{=}\highlight{9}\\ \highlight{-4}-2\amp\stackrel{?}{=}9\\ \highlight{-6}\amp\stackrel{\text{no}}{=}9 \end{align*}

So no, $-5$ is not a solution to $2(x+3)-2=4-x\text{.}$

Subsection2.9.3Solving One-Step Equations Review

Solving One-Step Equations

When we solve linear equations, we use Properties of Equivalent Equations and follow .

Example

Solve for $g$ in $\frac{1}{2}=\frac{2}{3}+g\text{.}$

We will subtract $\frac{2}{3}$ on both sides of the equation:

\begin{align*} \frac{1}{2}\amp=\frac{2}{3}+g\\ \frac{1}{2}\subtractright{\frac{2}{3}}\amp=\frac{2}{3}+g\subtractright{\frac{2}{3}}\\ \frac{3}{6}-\frac{4}{6}\amp=g\\ -\frac{1}{6}\amp=g \end{align*}

We will check the solution by substituting $g$ in the original equation with $-\frac{1}{6}\text{:}$

\begin{align*} \frac{1}{2}\amp=\frac{2}{3}+g\\ \frac{1}{2}\amp\stackrel{?}{=}\frac{2}{3}+\left(\substitute{-\frac{1}{6}}\right)\\ \frac{1}{2}\amp\stackrel{?}{=}\frac{4}{6}+\left(-\frac{1}{6}\right)\\ \frac{1}{2}\amp\stackrel{?}{=}\frac{3}{6}\\ \frac{1}{2}\amp\stackrel{\checkmark}{=}\frac{1}{2} \end{align*}

The solution $-\frac{1}{6}$ is checked and the solution set is $\left\{-\frac{1}{6}\right\}\text{.}$

Subsection2.9.4Solving One-Step Equations and Inequalities Review

Solving One-Step Inequalities

When we solve linear inequalities, we also use Properties of Equivalent Equations with one small complication: When we multiply or divide by the same negative number on both sides of an inequality, the direction reverses!

Example

Solve the inequality $-2x\geq12\text{.}$ State the solution set with both interval notation and set-builder notation.

To solve this inequality, we will divide each side by $-2\text{:}$

\begin{align*} -2x\amp\geq12\\ \divideunder{-2x}{-2}\amp\highlight{{}\leq{}}\divideunder{12}{-2}\amp\amp\text{Note the change in direction.}\\ x\amp\leq-6 \end{align*}

The inequality's solution set in interval notation is $(-\infty,-6]\text{.}$
The inequality's solution set in set-builder notation is $\{x\mid x\leq-6\}\text{.}$

Subsection2.9.5Solving One-Step Equations Involving Percentages Review

Solving One-Step Equations Involving Percentages

An important skill for solving percent-related problems is to boil down a complicated word problem into a simple form like “$2$ is $50\%$ of $4\text{.}$”

Example

What percent of $2346.19$ is $1995.98\text{?}$

Using $P$ to represent the unknown quantity, we write and solve the equation:

\begin{align*} \overbrace{\strut P}^{\text{what percent}}\overbrace{\strut \cdot}^{\text{of}} \overbrace{\strut 2346.19}^{\text{\$2346.19}}\amp\overbrace{\strut =}^{\text{is}}\overbrace{\strut 1995.98}^{\text{\$1995.98}}\\ \divideunder{P\cdot 2346.19}{2346.19}\amp=\divideunder{1995.98}{2346.19}\\ P\amp=0.85073\ldots\\ P\amp\approx85.07\% \end{align*}

In summary, $1995.98$ is approximately $85.07\%$ of $2346.19\text{.}$

Subsection2.9.6Modeling with Equations and Inequalities Review

Modeling with Equations and Inequalities

To set up an equation modeling a real world scenario, the first thing we need to do is identifying what variable we will use. The variable we use will be determined by whatever is unknown in our problem statement. Once we've identified and defined our variable, we'll use the numerical information provided in the equation to set up our equation.

Examples

A bathtub contains 2.5 ft³ of water. More water is being poured in at a rate of 1.75 ft³ per minute. When will the amount of water in the bathtub reach 6.25 ft³?

Since the question being asked in this problem starts with “when,” we immediately know that the unknown is time. As the volume of water in the tub is measured in ft³ per minute, we know that time needs to be measured in minutes. We'll defined $t$ to be the number of minutes that water is poured into the tub. Since each minute there are 1.75 ft³ of water added, we will add the expression $1.75t$ to $2.5$ to obtain the total amount of water. Thus the equation we set up is:

\begin{equation*} 2.5+1.75t=6.25 \end{equation*}

Subsection2.9.7Exponent Rules Review (Multiplication Only)

Rules of Exponents

Let $x,$ and $y$ represent real numbers, variables, or algebraic expressions, and let $m$ and $n$ represent positive integers. Then the following properties hold:

Product of Powers: $x^m\cdot x^n=x^{m+n}$
Power to Power: $(x^m)^n=x^{m\cdot n}$
Product to Power: $(xy)^n = x^n\cdot y^n$

Examples

Simplify the following expressions using the rules of exponents.

\begin{align*} -2t^3\cdot 4t^5\amp=-8t^8\\ 5\left(v^4\right)^2\amp=5v^8\\ -(3u)^2\amp=-9u^4\\ (-3u)^2\amp=9u^4 \end{align*}

Subsection2.9.8Simplifying Expressions Review

Algebraic Properties

Let $a,\text{,}$ $b\text{,}$ and $c$ represent real numbers, variables, or algebraic expressions. Then the following properties hold:

Commutative Property of Multiplication: \begin{equation} a\cdot b=b\cdot a\label{equation-commutative-property-multiplication}\tag{2.9.1} \end{equation}
Associative Property of Multiplication: \begin{equation*} a\cdot(b\cdot c)=(a\cdot b)\cdot c \end{equation*}
Commutative Property of Addition: \begin{equation*} a+b=b+a \end{equation*}
Associative Property of Addition: \begin{equation*} a+(b+c)=(a+b)+c \end{equation*}
Distributive Property: \begin{equation} a(b+c)=ab+ac\label{equation-distributive-property}\tag{2.9.2} \end{equation}

Examples

Use the associative, commutative, and distributive properties to simplify the following expression as much as possible:

\begin{equation*} 5x+9(-2x+3) \end{equation*}

We will remove parentheses by the distributive property, and then combine like terms:

\begin{align*} \amp=5x+9(-2x+3)\\ \amp=5x+9(-2x)+9(3)\\ \amp=5x-18x+27\\ \amp=-13x+27 \end{align*}

SubsectionExercises

1

A trapezoid’s area can be calculated by the formula $A=\frac{1}{2}(b_1+b_2)h\text{,}$ where $A$ stands for area, $b_1$ for the first base’s length, $b_2$ for the second base’s length, and $h$ for height.

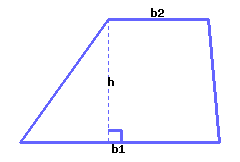
Use the formulas to calculate the trapezoid’s area. Its first base’s length is ${18\ {\rm m}}\text{,}$ its second base’s length is ${9\ {\rm m}}$ and its height is ${11\ {\rm m}}\text{.}$

Area =

2

To convert a temperature measured in degrees Fahrenheit to degrees Celsius, there is a formula:

$\displaystyle{ C={\frac{5}{9}\!\left(F-32\right)} }$

where $C$ represents the temperature in degrees Celsius and $F$ represents the temperature in degrees Fahrenheit.

If a temperature is $14 {^\circ}\text{F}\text{,}$ what is that temperature measured in Celsius?

3

Evaluate the expression ${x^{2}}\text{:}$

When $x=7\text{,}$ $\displaystyle{{x^{2}}=}$
When $x=-6\text{,}$ $\displaystyle{{x^{2}}=}$

4

Evaluate the expression ${y^{3}}\text{:}$

When $y=3\text{,}$ $\displaystyle{{y^{3}}=}$
When $y=-5\text{,}$ $\displaystyle{{y^{3}}=}$

5

Is $-1$ a solution for $x$ in the equation ${2x-1}={4-\left(8+x\right)}\text{?}$ Evaluating the left and right sides gives:

${2x-1}$	$=$	${4-\left(8+x\right)}$
	${}\stackrel{?}{=}{}$

So $-1$

is
is not

a solution to ${2x-1}={4-\left(8+x\right)}\text{.}$

6

Is $2$ a solution for $x$ in the inequality ${-2x^{2}+x}\le{-2x+4}\text{?}$ Evaluating the left and right sides gives:

${-2x^{2}+x}$	$\le$	${-2x+4}$
	${}\stackrel{?}{\le}{}$

So $2$

is
is not

a solution to ${-2x^{2}+x}\le{-2x+4}\text{.}$

7

Solve the equation.

$\displaystyle{ {r+4}={-5} }$

8

Solve the equation.

$\displaystyle{ {6}={-1+t} }$

9

Solve the equation.

$\displaystyle{ {t+{\frac{1}{8}}}={{\frac{7}{8}}} }$

10

Solve the equation.

$\displaystyle{ {56}={-8t} }$

11

Solve the equation.

$\displaystyle{ {{\frac{7}{9}}y}={14} }$

12

The pie chart represents a collector’s collection of signatures from various artists.

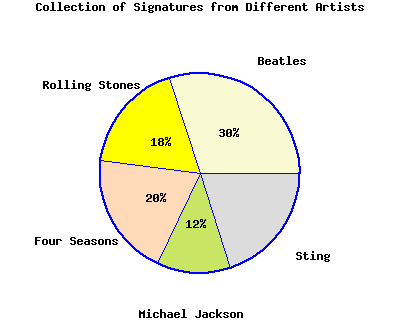
If the collector has a total of $650$ signatures, there are signatures by Sting.

13

A community college conducted a survey about the number of students riding each bus line available. The following bar graph is the result of the survey.

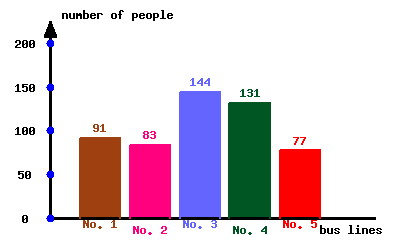
What percent of students ride Bus No. 1?

Fill in the blank with a percent. Round your percent to whole numbers, like $11\%\text{.}$

Approximately of students ride Bus No. 1.

14

The following is a nutrition fact label from a certain macaroni and cheese box.

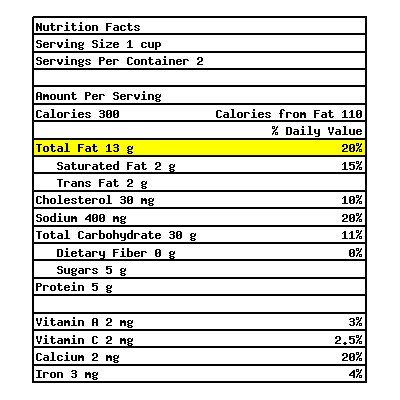
The highlighted row means each serving of macaroni and cheese in this box contains ${13\ {\rm g}}$ of fat, which is $20\%$ of an average person’s daily intake of fat. What’s the recommended daily intake of fat for an average person?

The recommended daily intake of fat for an average person is .

Use g for grams.

15

Ashley used to make $15$ dollars per hour. After she earned her Bachelor’s degree, her pay rate increased to $53$ dollars per hour. What is the percentage increase in Ashley’s salary?

The percentage increase is .

16

After a $20\%$ increase, a town has $720$ people. What was the population before the increase?

Before the increase, the town’s population was .

17

A bicycle for sale costs ${\$258.24}\text{,}$ which includes $7.6\%$ sales tax. What was the cost before sales tax?

Assume the bicycle’s price before sales tax is $p$ dollars. Write an equation to model this scenario. There is no need to solve it.

18

The property taxes on a $1900$-square-foot house are ${\$3{,}534.00}$ per year. Assuming these taxes are proportional, what are the property taxes on a $2300$-square-foot house?

Assume property taxes on a $2300$-square-foot house is $t$ dollars. Write an equation to model this scenario. There is no need to solve it.

19

A swimming pool is being filled with water from a garden hose at a rate of $6$ gallons per minute. If the pool already contains $100$ gallons of water and can hold $184$ gallons, after how long will the pool overflow?

Assume $m$ minutes later, the pool would overflow. Write an equation to model this scenario. There is no need to solve it.

20

Use the distributive property to simplify ${9-5\!\left(4-8y\right)}$ completely.

21

Use the properties of exponents to simplify the expression.

$({-2t^{5}})\cdot({3t^{11}})$

22

Use the properties of exponents to simplify the expression.

$\displaystyle{{\left(-2a\right)^{2}}=}$

$\displaystyle{{-\left(2a\right)^{2}}=}$

23

Find the product of the monomial and the binomial.

${9y^{2}}\left({-9y^{2}-10y}\right)=$

\({2x-1}\)	\(=\)	\({4-\left(8+x\right)}\)
	\({}\stackrel{?}{=}{}\)

\({-2x^{2}+x}\)	\(\le\)	\({-2x+4}\)
	\({}\stackrel{?}{\le}{}\)