Section4.8Horizontal, Vertical, Parallel, and Perpendicular Lines
Ā¶Horizontal and vertical lines have some special features worth our attention. Also if a pair of lines are parallel or perpendicular to each other, we have some interesting things to say about them. This section looks at these geometric features that lines may have.
Subsection4.8.1Horizontal Lines and Vertical Lines
We learned in SectionĀ 4.7 that all lines can be written in standard formĀ (4.7.1). When either \(A\) or \(B\) equal \(0\text{,}\) we end up with a horizontal or vertical line, as we will soon see. Let's take the standard formĀ (4.7.1) line equation, let \(A=0\) and \(B=0\) one at a time and simplify each equation.
\begin{align*}
Ax+By\amp=C\amp Ax+By\amp=C\\
\substitute{0}x+By\amp=C\amp Ax+\substitute{0}y\amp=C\\
By\amp=C\amp Ax\amp=C\\
y\amp=\divideunder{C}{B}\amp x\amp=\divideunder{C}{A}\\
y\amp=k\amp x\amp=h
\end{align*}
At the end we just renamed the constant numbers \(\frac{C}{B}\) and \(\frac{C}{A}\) to \(k\) and \(h\) because of tradition. What is important, is that you view \(h\) and \(k\) (as well as \(A\text{,}\) \(B\text{,}\) and \(C\)) as constants: numbers that have some specific value and don't change in the context of one problem.
Think about just one of these last equations: \(y=k\text{.}\) It says that the \(y\)-value is the same no matter where you are on the line. If you wanted to plot points on this line, you are free to move far to the left or far to the right on the \(x\)-axis, but then you always move up (or down) to make the \(y\)-value equal \(k\text{.}\) What does such a line look like?
Example4.8.6
Let's plot the line with equation \(y=3\text{.}\) (Note that this is the same as \(0x+1y=3\text{.}\))
To plot some points, it doesn't matter what \(x\)-values we use. All that matters is that \(y\) is always \(3\text{.}\)
A line like this is horizontal, parallel to the horizontal axis. All lines with an equation in the form
\begin{equation*}
y=k
\end{equation*}
(or, in standard form, \(0x+By=C\)) are horizontal.
Example4.8.8
Let's plot the line with equation \(x=5\text{.}\) (Note that this is the same as \(1x+0y=5\text{.}\))
The line has \(x=5\text{,}\) so to plot points, we are required to move over to \(x=5\text{.}\) From there, we have complete freedom to move however far we like up or down.
A line like this is vertical, parallel to the vertical axis. All lines with an equation in the form
\begin{equation*}
x=h
\end{equation*}
(or, in standard form, \(Ax+0y=C\)) are vertical.
Example4.8.10Zero Slope
In CheckpointĀ 4.4.22, we learned that a horizontal line's slope is \(0\text{,}\) because the distance doesn't change as time moves on. So the numerator in the slope formulaĀ (4.4.3) is \(0\text{.}\) Now, if we know a line's slope and its \(y\)-intercept, we can use slope-intercept formĀ (4.5.1) to write its equation:
\begin{align*}
y\amp=mx+b\\
y\amp=0x+b\\
y\amp=b
\end{align*}
This provides us with an alternative way to think about equations of horizontal lines. They have a certain \(y\)-intercept \(b\text{,}\) and they have slope \(0\text{.}\)
We use horizontal lines to model scenarios where there is no change in \(y\)-values, like when Tammy stopped for \(12\) hours (she deserved a rest!)
Checkpoint4.8.11Plotting Points
Example4.8.12Undefined Slope
What is the slope of a vertical line? FigureĀ 4.8.13 shows three lines passing through the origin, each steeper than the last. In each graph, you can see a slope triangle that uses a āriseā of \(4\) each time.
If we continued making the line steeper and steeper until it was vertical, the slope triangle would still have a āriseā of \(4\text{,}\) but the ārunā would become smaller and smaller, closer to \(0\text{.}\) And then the slope would be \(m=\frac{4}{\text{very small}}=\text{very large}\text{.}\) So the slope of a vertical line can be thought of as āinfinitely large.ā
If we actually try to compute the slope using the slope triangle when the run is \(0\text{,}\) we would have \(\frac{4}{0}\text{,}\) which is undefined. So we also say that the slope of a vertical line is undefined. Some people say that a vertical line has no slope.
Remark4.8.14
Be careful not to mix up āno slopeā (which means āits slope is undefinedā) with āhas slope \(0\text{.}\)ā If a line has slope \(0\text{,}\) it does have a slope.
Checkpoint4.8.15Plotting Points
Example4.8.16
Let \(x\) represent the price of a new \(60\)-inch television at Target on Black Friday (which was \(\$650\)), and let \(y\) be the number of hours you will watch something on this TV over its lifetime. What is the relationship between \(x\) and \(y\text{?}\)
Well, there is no getting around the fact that \(x=650\text{.}\) As for \(y\text{,}\) without any extra information about your viewing habits, it could theoretically be as low as \(0\) or it could be anything larger than that. If we graph this scenario, we have to graph the equation \(x=650\) which we now know to give a vertical line, and we get FigureĀ 4.8.17.
Theorem4.8.18Summary of Horizontal and Vertical Line Equations
| Horizontal Lines | Vertical Lines |
|
A line is horizontal if and only if its equation can be written
\begin{equation*}
y=k
\end{equation*}
for some constant \(k\text{.}\) |
A line is vertical if and only if its equation can be written
\begin{equation*}
x=h
\end{equation*}
for some constant \(h\text{.}\) |
|
In standard formĀ (4.7.1), any line with equation
\begin{equation*}
0x+By=C
\end{equation*}
is horizontal. |
In standard formĀ (4.7.1), any line with equation
\begin{equation*}
Ax+0y=C
\end{equation*}
is vertical. |
If the line with equation \(y=k\) is horizontal, it has a \(y\)-intercept at \((0,k)\) and has slope \(0\text{.}\) |
If the line with equation \(x=h\) is vertical, it has an \(x\)-intercept at \((h,0)\) and its slope is undefined. Some say it has no slope, and some say the slope is infinitely large. |
|
In slope-intercept formĀ (4.5.1), any line with equation
\begin{equation*}
y=0x+b
\end{equation*}
is horizontal. |
It's impossible to write the equation of a vertical line in slope-intercept formĀ (4.5.1), because vertical lines do not have a defined slope. |
Subsection4.8.2Parallel Lines
Ā¶Example4.8.19
Two trees were planted in the same year, and their growth over time is modeled by the two lines in FigureĀ 4.8.20. Use linear equations to model each tree's growth, and interpret their meanings in this context.
We can see Tree 1's equation is \(y=\frac{2}{3}x+2\text{,}\) and Tree 2's equation is \(y=\frac{2}{3}x+5\text{.}\) Tree 1 was \(2\) feet tall when it was planted, and Tree 2 was \(5\) feet tall when it was planted. Both trees have been growing at the same rate, \(\frac{2}{3}\) feet per year, or \(2\) feet every \(3\) years.
An important observation right now is that those two lines are parallel. Why? For lines with positive slopes, the bigger a line's slope, the steeper the line is slanted. As a result, if two lines have the same slope, they are slanted at the same angle, thus they are parallel.
Fact4.8.21
Any two vertical lines are parallel to each other. For two non-vertical lines, they are parallel if and only if they have the same slope.
Checkpoint4.8.22
Checkpoint4.8.23
Subsection4.8.3Perpendicular Lines
The slopes of two perpendicular lines have a special relationship too.
FigureĀ 4.8.26 walks you through an explanation of this relationship.
The second line in FigureĀ 4.8.26 has slope
\begin{equation*}
\frac{\Delta y}{\Delta x}=\frac{-1}{m}=-\frac{1}{m}\text{.}
\end{equation*}
Fact4.8.27
A vertical line and a horizontal line are perpendicular. For lines that are neither vertical nor horizontal, they are perpendicular if and only if the slope of one is the negative reciprocal of the slope of the other. That is, if one has slope \(m\text{,}\) the other has slope \(-\frac{1}{m}\text{.}\)
Another way to say this is that the product of the slopes of two perpendicular lines is \(-1\) (assuming both of the lines have a slope in the first place).
Not convinced? Here are three pairs of perpendicular lines where we can see if the pattern holds.
Example4.8.31
Line \(A\) passes through \((-2,10)\) and \((3,-10)\text{.}\) Line \(B\) passes through \((-4,-4)\) and \((8,-1)\text{.}\) Determine whether these two lines are parallel, perpendicular or neither.
Solution
We will use the slope formula to find both lines' slopes:
\begin{align*}
\text{Line }A\text{'s slope}\amp=\frac{y_2-y_1}{x_2-x_1}\amp\text{Line }B\text{'s slope}\amp=\frac{y_2-y_1}{x_2-x_1}\\
\amp=\frac{-10-10}{3-(-2)}\amp\amp=\frac{-1-(-4)}{8-(-4)}\\
\amp=\frac{-20}{5}\amp\amp=\frac{3}{12}\\
\amp=-4\amp\amp=\frac{1}{4}
\end{align*}
Their slopes are not the same, so those two lines are not parallel.
The product of their slopes is \((-4)\cdot\frac{1}{4}=-1\text{,}\) which means the two lines are perpendicular.
Checkpoint4.8.32
SubsectionExercises
Creating tables for horizontal and vertical lines.
1
Fill out this table for the equation \(y=2\text{.}\) The first row is an example.
| \(x\) | \(y\) | Points |
| \(-3\) | \(2\) | \(\left(-3,2\right)\) |
| \(-2\) | ||
| \(-1\) | ||
| \(0\) | ||
| \(1\) | ||
| \(2\) |
2
Fill out this table for the equation \(y=4\text{.}\) The first row is an example.
| \(x\) | \(y\) | Points |
| \(-3\) | \(4\) | \(\left(-3,4\right)\) |
| \(-2\) | ||
| \(-1\) | ||
| \(0\) | ||
| \(1\) | ||
| \(2\) |
3
Fill out this table for the equation \(x=-6\text{.}\) The first row is an example.
| \(x\) | \(y\) | Points |
| \(-6\) | \(-3\) | \(\left(-6,-3\right)\) |
| \(-2\) | ||
| \(-1\) | ||
| \(0\) | ||
| \(1\) | ||
| \(2\) |
4
Fill out this table for the equation \(x=-5\text{.}\) The first row is an example.
| \(x\) | \(y\) | Points |
| \(-5\) | \(-3\) | \(\left(-5,-3\right)\) |
| \(-2\) | ||
| \(-1\) | ||
| \(0\) | ||
| \(1\) | ||
| \(2\) |
Determining whether a point is on a horizontal or vertical line.
5
Consider the equation \(y=1\text{.}\)
Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.
\( (-9,1)\)
\( (1,5)\)
\( (7,1)\)
\( (0,9)\)
6
Consider the equation \(y=1\text{.}\)
Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.
\( (8,1)\)
\( (0,7)\)
\( (-3,1)\)
\( (1,3)\)
7
Consider the equation \(x+1=0\text{.}\)
Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.
\( (0,-5)\)
\( (-1,5)\)
\( (1,-1)\)
\( (-1,0)\)
8
Consider the equation \(x+1=0\text{.}\)
Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.
\( (0,-7)\)
\( (-1,5)\)
\( (1,-1)\)
\( (-1,0)\)
Given two points, find the equations of the line connecting them.
9
A line passes through the points \((-3,-9)\) and \((-1,-9)\text{.}\) Find an equation for this line.
An equation for this line is .
10
A line passes through the points \((4,-7)\) and \((3,-7)\text{.}\) Find an equation for this line.
An equation for this line is .
11
A line passes through the points \((-4,0)\) and \((-4,-3)\text{.}\) Find an equation for this line.
An equation for this line is .
12
A line passes through the points \((-2,-3)\) and \((-2,1)\text{.}\) Find an equation for this line.
An equation for this line is .
Given linear graphs, find the equations of horizontal and vertical lines.
13
A lineās graph is given.
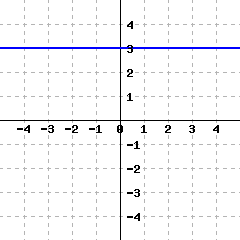
This lineās equation is
14
A lineās graph is given.
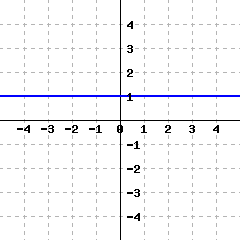
This lineās equation is
15
A lineās graph is given.
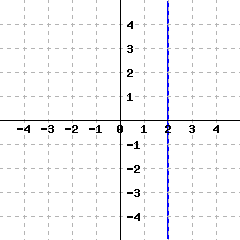
This lineās equation is
16
A lineās graph is given.
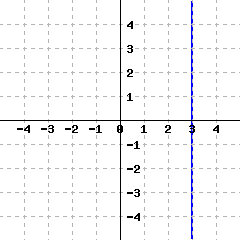
This lineās equation is
Finding the intercepts of horizontal and vertical lines.
17
Find the \(y\)-intercept and \(x\)-intercept of the line given by the equation
\(\displaystyle{x = 10}\)
If a particular intercept does not exist, enter none into all the answer blanks for that row.
| \(x\)-value | \(y\)-value | Location | |
| \(y\)-intercept | |||
| \(x\)-intercept |
18
Find the \(y\)-intercept and \(x\)-intercept of the line given by the equation
\(\displaystyle{x = -9}\)
If a particular intercept does not exist, enter none into all the answer blanks for that row.
| \(x\)-value | \(y\)-value | Location | |
| \(y\)-intercept | |||
| \(x\)-intercept |
19
Find the \(y\)-intercept and \(x\)-intercept of the line given by the equation
\(\displaystyle{y = -7}\)
If a particular intercept does not exist, enter none into all the answer blanks for that row.
| \(x\)-value | \(y\)-value | Location | |
| \(y\)-intercept | |||
| \(x\)-intercept |
20
Find the \(y\)-intercept and \(x\)-intercept of the line given by the equation
\(\displaystyle{y = -4}\)
If a particular intercept does not exist, enter none into all the answer blanks for that row.
| \(x\)-value | \(y\)-value | Location | |
| \(y\)-intercept | |||
| \(x\)-intercept |
Given their equation, graph horizontal and vertical lines.
21
Graph the line \(y=1\text{.}\)
22
Graph the line \(y+5=0\text{.}\)
23
Graph the line \(x=2\text{.}\)
24
Graph the line \(x-3=0\text{.}\)
Finding equations of parallel lines.
25
A line passes through the point \((-3,-9)\text{,}\) and itās parallel to the line \(y=-2\text{.}\) Find an equation for this line.
An equation for this line is .
26
A line passes through the point \((6,4)\text{,}\) and itās parallel to the line \(y=0\text{.}\) Find an equation for this line.
An equation for this line is .
27
A line passes through the point \((-3,-6)\text{,}\) and itās parallel to the line \(x=3\text{.}\) Find an equation for this line.
An equation for this line is .
28
A line passes through the point \((-10,3)\text{,}\) and itās parallel to the line \(x=5\text{.}\) Find an equation for this line.
An equation for this line is .
29
Line \(k\) has the equation \(y={4x+6}\text{.}\)
Line \(\ell\) is parallel to line \(k\text{,}\) but passes through the point \((-5,-18)\text{.}\)
Find an equation for line \(\ell\) in both slope-intercept form and point-slope form.
An equation for \(\ell\) in slope-intercept form is: .
An equation for \(\ell\) in point-slope form is: .
30
Line \(k\) has the equation \(y={5x-3}\text{.}\)
Line \(\ell\) is parallel to line \(k\text{,}\) but passes through the point \((-1,-7)\text{.}\)
Find an equation for line \(\ell\) in both slope-intercept form and point-slope form.
An equation for \(\ell\) in slope-intercept form is: .
An equation for \(\ell\) in point-slope form is: .
31
Line \(k\) has the equation \(y={-{\frac{1}{9}}x+5}\text{.}\)
Line \(\ell\) is parallel to line \(k\text{,}\) but passes through the point \((-27,{7})\text{.}\)
Find an equation for line \(\ell\) in both slope-intercept form and point-slope form.
An equation for \(\ell\) in slope-intercept form is: .
An equation for \(\ell\) in point-slope form is: .
32
Line \(k\) has the equation \(y={-{\frac{2}{7}}x+5}\text{.}\)
Line \(\ell\) is parallel to line \(k\text{,}\) but passes through the point \((14,{-6})\text{.}\)
Find an equation for line \(\ell\) in both slope-intercept form and point-slope form.
An equation for \(\ell\) in slope-intercept form is: .
An equation for \(\ell\) in point-slope form is: .
Determining whether Two Lines Are Parallel or Perpendicular
33
Line \(m\) passes points \((2,-1)\) and \((3,1)\text{.}\)
Line \(n\) passes points \((5,0)\) and \((-5,-20)\text{.}\)
Determine how the two lines are related.
These two lines are
parallel
perpendicular
neither parallel nor perpendicular
34
Line \(m\) passes points \((-18,0)\) and \((18,-16)\text{.}\)
Line \(n\) passes points \((-45,20)\) and \((-18,8)\text{.}\)
Determine how the two lines are related.
These two lines are
parallel
perpendicular
neither parallel nor perpendicular
35
Line \(m\) passes points \((12,-1)\) and \((4,1)\text{.}\)
Line \(n\) passes points \((-4,-26)\) and \((3,2)\text{.}\)
Determine how the two lines are related.
These two lines are
parallel
perpendicular
neither parallel nor perpendicular
36
Line \(m\) passes points \((-14,16)\) and \((-7,10)\text{.}\)
Line \(n\) passes points \((-6,-1)\) and \((18,27)\text{.}\)
Determine how the two lines are related.
These two lines are
parallel
perpendicular
neither parallel nor perpendicular
37
Line \(m\) passes points \((-1,10)\) and \((2,4)\text{.}\)
Line \(n\) passes points \((1,-3)\) and \((3,-1)\text{.}\)
Determine how the two lines are related.
These two lines are
parallel
perpendicular
neither parallel nor perpendicular
38
Line \(m\) passes points \((1,7)\) and \((6,7)\text{.}\)
Line \(n\) passes points \((4,-8)\) and \((0,-8)\text{.}\)
Determine how the two lines are related.
These two lines are
parallel
perpendicular
neither parallel nor perpendicular
39
Line \(m\) passes points \((10,-6)\) and \((10,7)\text{.}\)
Line \(n\) passes points \((3,10)\) and \((3,0)\text{.}\)
Determine how the two lines are related.
These two lines are
parallel
perpendicular
neither parallel nor perpendicular
40
Line \(m\) passes points \((-9,7)\) and \((-9,3)\text{.}\)
Line \(n\) passes points \((1,3)\) and \((1,0)\text{.}\)
Determine how the two lines are related.
These two lines are
parallel
perpendicular
neither parallel nor perpendicular
Find a Line's Equation Perpendicular to a Given Equation
41
Line \(k\) has the equation \(y={-x-10}\text{.}\)
Line \(\ell\) is perpendicular to line \(k\text{,}\) and passes through the point \((1,-1)\text{.}\)
Find an equation for line \(\ell\) in both slope-intercept form and point-slope form.
An equation for \(\ell\) in slope-intercept form is: .
An equation for \(\ell\) in point-slope form is: .
42
Line \(k\) has the equation \(y={-3x-5}\text{.}\)
Line \(\ell\) is perpendicular to line \(k\) and passes through the point \((6,{3})\text{.}\)
Find an equation for \(\ell\) in both slope-intercept form and point-slope forms.
An equation for \(\ell\) in slope-intercept form is: .
An equation for \(\ell\) in point-slope form is: .
43
Line \(k\)ās equation is \(y={{\frac{5}{8}}x+3}\text{.}\)
Line \(\ell\) is perpendicular to line \(k\) and passes through the point \((15,{-23})\text{.}\)
Find an equation for line \(\ell\) in both slope-intercept form and point-slope forms.
An equation for \(\ell\) in slope-intercept form is: .
An equation for \(\ell\) in point-slope form is: .
44
Line \(k\) has the equation \({x+6y}=-12\text{.}\)
Line \(\ell\) is perpendicular to line \(k\) and passes through the point \((5,{31})\text{.}\)
Find line \(\ell\)ās equation in both slope-intercept form and point-slope form.
An equation for \(\ell\) in slope-intercept form is: .
An equation for \(\ell\) in point-slope form is: .