ORCCA Graphs and Vertex Form

Section12.1Graphs and Vertex Form

In this section, we will explore quadratic functions using graphing technology and learn the vertex and factored forms of a parabola. We will also see how parabolas can be shifted horizontally and vertically.

Figure12.1.1Alternative Video Lessons

Subsection12.1.1Exploring Quadratic Functions with Graphing Technology

Graphing technology is very important and useful for applications and for finding points quickly. Let's explore some quadratic functions with graphing technology.

Example12.1.2

Use technology to graph and make a table of the quadratic function \(f\) defined by \(f(x)=2x^2+4x-3\) and find each of the key points or features.

Find the vertex.
Find the vertical intercept or \(y\)-intercept.
Find the horizontal or \(x\)-intercept(s).
Find \(f(-2)\text{.}\)
Solve \(f(x)=3\) using the graph.
Solve \(f(x)\le 3\) using the graph.
State the domain and range of the function.

Solution

The specifics of how to use any one particular technology tool vary. Whether you use an app, a physical calculator, or something else, a table and graph should look like:

\(x\)	\(f(x)\)
\(-2\)	\(-3\)
\(-1\)	\(-5\)
\(0\)	\(-3\)
\(1\)	\(3\)
\(2\)	\(13\)

the graph of the parabola f(x)=2x^2+4x-3, that opens upward, passing through the points listed in the table

Additional features of your technology tool can enhance the graph to help answer these questions. You may be able to make the graph appear like:

the previous graph with all of the key points labeled as described below

The vertex is \((-1,-5)\text{.}\)
The vertical intercept is \((0,-3)\text{.}\)
The horizontal intercepts are approximately \((-2.6,0)\) and \((0.6,0)\text{.}\)
When \(x=-2\text{,}\) \(y=-3\text{,}\) so \(f(-2)=-3\text{.}\)
The solutions to \(f(x)=3\) are the \(x\)-values where \(y=3\text{.}\) We graph the horizontal line \(y=3\) and find the \(x\)-values where the graphs intersect. The solution set is \(\{-3,1\}\text{.}\)
The solutions are all \(x\)-values where the function below (or touching) the line \(y=3\text{.}\) The interval is \([-3,1]\text{.}\)
The domain is \((-\infty,\infty)\) and the range is \([-5,\infty)\text{.}\)

Now we will look at an application with graphing technology and put the points of interest in context.

Example12.1.3

A reduced-gravity aircraft ¹en.wikipedia.org/wiki/Reduced-gravity_aircraft is a fixed-wing airplane that astronauts use for training. The airplane flies up and then down in a parabolic path to simulate the feeling of weightlessness. In one training flight, the pilot will fly about 40–60 parabolic maneuvers.

For the first parabolic maneuver, the altitude of the plane, in feet, at time \(t\text{,}\) in seconds since the maneuver began, is given by \(H(t)=-16t^2+400t+30500\text{.}\)

Determine the starting altitude of the plane for the first maneuver.
What is the altitude of the plane \(10\) seconds into the maneuver?
Determine the maximum altitude of the plane and how long it takes to reach that altitude.
The zero-gravity effect is experienced when the plane begins the parabolic path until it gets back down to \(30{,}500\) feet. Write an inequality to express this and solve it using the graph. Write the times of the zero-gravity effect as an interval and determine how long the astronauts experience weightlessness during each cycle.
Use technology to make a table for \(H\) with \(t\)-values from \(0\) to \(25\) seconds. Use an increment of \(5\) seconds and then use the table to solve \(H(t)=32100\text{.}\)
State the domain and range for this context.

Solution

We can answer the questions based on the information in the graph.

a graph of the parabola y=-16t^2+400t+30500 and the horizontal line y=30500; the parabola opens downward and has a maximum at (12.5, 33000) — Figure12.1.4Graph of \(H(t)=-16t^2+400t+30500\) with \(y=30500\)

The starting altitude is the vertical intercept, which is \((0,30500)\text{.}\) The feeling of weightlessness begins at \(30{,}500\) feet.
After \(10\) seconds, the altitude of the plane is \(32{,}900\) feet.
For the maximum altitude of the plane we look at the vertex, which is approximately \((12.5, 33000)\text{.}\) This tells us that after \(12.5\) seconds the plane will be at its maximum altitude of \(33,000\) feet.
We can write an inequality to describe when the plane is at or above \(30{,}500\) feet and solve it graphically.

\begin{equation*} -16t^2+400t+30500\ge30500\text{.} \end{equation*}

We graph the line \(y=30500\) and find the points of intersection with the parabola. The astronauts experience weightlessness from \(0\) seconds to \(25\) seconds into the maneuver, or \([0,25]\) seconds. They experience weightlessness for 25 seconds in each cycle.
To solve \(H(t)=32100\) using the table, we look for where the \(H\)-values are equal to \(32100\text{.}\) There are two solutions, \(5\) seconds and \(20\) seconds. The solution set is \(\{5,20\}\text{.}\)

\(t\) \(0\) \(5\) \(10\) \(15\) \(20\) \(25\)

\(H(t)\) \(30500\) \(32100\) \(32900\) \(32900\) \(32100\) \(30500\)
When we use graphing technology we see the entire function but in this context the plane is only on a parabolic path from \([0,25]\) seconds, which is the domain, and the range of \([30500,33000]\) feet.

Let's look at the remote-controlled airplane dive from Example 9.3.18. This time we will use technology to answer the questions.

Example12.1.5

The owner of a remote-controlled airplane is going to do a stunt dive where the plane dives toward the ground and back up along a parabolic path. The altitude of the plane is given by the function \(H\) where \(H(t)=0.7t^2-23t+200\text{,}\) for \(0 \le t \le 30\text{.}\) The altitude is measured in feet and the time, \(t\text{,}\) is measured in seconds since the stunt began.

Determine the starting altitude of the plane as the dive begins.
Determine the altitude of the plane after \(5\) seconds.
Will the plane hit the ground, and if so, at what time?
If the plane does not hit the ground, what is the closest it gets to the ground, and at what time?
At what time(s) will the plane have a altitude of \(50\) feet?
State the domain and the range of the function in interval form and in context.

Solution

We have graphed the function and we will find the key information and put it in context.

a graph of the quadratic function with all of the key features labeled that are described below — Figure12.1.6Graph of \(H(t)=0.7t^2-23t+200\)

The starting altitude is the vertical intercept, which is \((0,200)\text{.}\) When the stunt begins, the plane has a altitude of \(200\) feet.
When \(x=5\text{,}\) the \(y\)-value is \(102.5\text{,}\) or \(H(5)=102.5\text{.}\) This means that after \(5\) seconds, the plane is \(102.5\) feet above the ground.
From the graph we can see that the parabola does not touch or cross the \(x\)-axis, which represents the ground. This means the plane does not hit the ground and there are no real solutions to the equation \(H(t)=0\text{.}\)
The lowest point is the vertex, which is approximately \((16.43, 11.07)\text{.}\) The minimum altitude of the plane is about \(11\) feet, which occurs after about \(16.4\) seconds.
We will graph the horizontal line \(y=50\) and look for the points of intersection. The plane will be \(50\) feet above the ground about 9 seconds and 24 seconds after the plane begins the stunt.
The domain for this problem is given in the problem statement because only part of the parabola represents the path of the plane. The domain is \([0,30]\text{.}\) For the range we look at the possible altitudes of the plane and see that it is \([11,200]\text{.}\) The plane is doing this stunt from \(0\) to \(30\) seconds and its height ranges from about \(11\) to \(200\) feet above the ground.

Subsection12.1.2The Vertex Form of a Parabola

We have learned the standard form of quadratic functions, which is \(f(x)=ax^2+bx+c\text{.}\) In this subsection, we will learn another form called the vertex form.

Using graphing technology, we will graph \(f(x)=x^2-6x+7\) and \(g(x)=(x-3)^2-2\) on the same axes.

the graphs of the two parabolas overlap each other completely — Figure12.1.7Graph of \(f(x)=x^2-6x+7\) and \(g(x)=(x-3)^2-2\)

We see only one parabola because these are two different forms of the same function. We can see this if we convert \(g(x)\) into standard form.

\begin{align*} g(x)\amp=(x-3)^2-2\\ g(x)\amp=(x-3)(x-3)-2\\ g(x)\amp=x^2-6x+9-2\\ g(x)\amp=x^2-6x+7 \end{align*}

Now it is clear that \(f\) and \(g\) are the same function.

The formula given for \(g\) is written in vertex form which is very useful because it allows us to read the vertex without doing any calculations. The vertex of the parabola is \((3,-2)\text{.}\) We can see those numbers in \(g(x)=(x-3)^2-2\text{.}\) The \(x\)-value is the solution to \((x-3)=0\text{,}\) and the \(y\)-value is the constant added at the end.

Here are the graphs of three more functions in vertex form. Compare each function with the vertex of its graph.

the graph of a parabola that opens upward and has a vertex at (2,1)

the graph of a wide parabola that opens downward and has a vertex at (-1,3)

the graph of a narrow parabola that opens upward and has a vertex at (-3,-3.5)

Figure12.1.8The graph of \(r(x)=(x-2)^2+1\)

Figure12.1.9The graph of \(s(x)=-\frac{1}{4}(x+1)^2+3\)

Figure12.1.10The graph of \(t(x)=4(x+3)^2-3.5\)

Notice that the \(x\)-coordinate of the vertex has the opposite sign as the value in the function formula. On the other hand, the \(y\)-coordinate of the vertex has the same sign as the value in the function formula. Let's look at an example to understand why. We will substitute \(x=2\) into \(r(x)\) from Figure 12.1.8.

\begin{align*} r(x)\amp=(x-2)^2+1\\ r(\substitute{2})\amp=(\substitute{2}-2)^2+1\\ \amp=(0)^2+1\\ \amp=1 \end{align*}

The \(x\)-value is the solution to \((x-2)=0\text{,}\) which is positive \(2\text{.}\) When we substitute \(\substitute{2}\) for \(x\) we get the value \(y=1\text{.}\) Note that these coordinates create the vertex at \((2,1)\text{.}\) Now we can define the vertex form of a quadratic function.

Fact12.1.11Vertex Form of a Quadratic Function

A quadratic function with the vertex at the point \((h,k)\) is given by \(f(x)=a(x-h)^2+k\text{.}\)

Now you can try reading the vertex of each function.

Example12.1.12

Find the vertex of each quadratic function.

\(r(x)=-2(x+4)^2+10\)
\(s(x)=5(x-1)^2+2\)
\(t(x)=(x-10)^2-5\)
\(u(x)=3(x+7)^2-13\)

Solution

The vertex of \(r(x)=-2(x\highlight{+4})^2\lighthigh{+10}\) is \((\highlight{-4},\lighthigh{10})\text{.}\)
The vertex of \(s(x)=5(x\highlight{-1})^2\lighthigh{+2}\) is \((\highlight{1},\lighthigh{2})\text{.}\)
The vertex of \(t(x)=(x\highlight{-10})^2\lighthigh{-5}\) is \((\highlight{10},\lighthigh{-5})\text{.}\)
The vertex of \(u(x)=3(x\highlight{+7})^2\lighthigh{-13}\) is \((\highlight{-7},\lighthigh{-13})\text{.}\)

Now let's do the reverse. When given the vertex and the value of \(a\text{,}\) we can write the function in vertex form.

Example12.1.13

Write a formula for the quadratic function \(f\) with the given vertex and value of \(a\text{.}\)

Vertex \((-2,8)\text{,}\) \(a=1\)
Vertex \((4,-9)\text{,}\) \(a=-4\)
Vertex \((-3,-1)\text{,}\) \(a=2\)
Vertex \((5,12)\text{,}\) \(a=-3\)

Solution

The vertex form is \(f(x)=(x+2)^2+8\text{.}\)
The vertex form is \(f(x)=-4(x-4)^2-9\text{.}\)
The vertex form is \(f(x)=2(x+3)^2-1\text{.}\)
The vertex form is \(f(x)=-3(x-5)^2+12\text{.}\)

Once we read the vertex we can also state the domain and range. All parabolas have a domain of \((-\infty,\infty)\) because we can put in any value to a quadratic function. The range, however, depends on the \(y\)-value of the vertex and whether the parabola opens upward or downward. When we have a parabola in vertex form we can read the range from the function. Let's look at the graph of \(f(x)=2(x-3)^2-5\) as an example.

the graph of a parabola that opens upward with a vertex of (3,-5) — Figure12.1.14The graph of \(f(x)=2(x-3)^2-5\)

The domain is \((-\infty,\infty)\text{.}\) The graph of \(f\) opens upward so the vertex is the minimum point. The \(y\)-value of \(-5\) is the minimum. The range is \([-5,\infty)\text{.}\)

Example12.1.15

Identify the domain and range of \(g\text{,}\) where \(g(x)=-3(x+1)^2+6\text{.}\)

Solution

the graph of a parabola that opens downward with a vertex of (-1,6) — Figure12.1.16The graph of \(g(x)=-3(x+1)^2+6\)

The domain is \((-\infty,\infty)\text{.}\) The graph of \(g\) opens downward so the vertex is the maximum point. The \(y\)-value of \(6\) is the maximum. The range is \((-\infty,6]\text{.}\)

Example12.1.17

Identify the domain and range of each quadratic function.

\(w(x)=-3(x+10)^2-11\)
\(x(x)=4(x-7)^2+20\)
\(y(x)=-(x-1)^2\)
\(z(x)=3(x+9)^2-4\)

Solution

The domain of \(w\) is \((-\infty,\infty)\text{.}\) The parabola opens downward so the range is \((-\infty,-11]\text{.}\)
The domain of \(x\) is \((-\infty,\infty)\text{.}\) The parabola opens upward so the range is \([20,\infty)\text{.}\)
The domain of \(y\) is \((-\infty,\infty)\text{.}\) The parabola opens downward so the range is \((-\infty,0]\text{.}\)
The domain of \(z\) is \((-\infty,\infty)\text{.}\) The parabola opens upward so the range is \([-4,\infty)\text{.}\)

Subsection12.1.3Horizontal and Vertical Shifts

Let \(f(x)=x^2\) and \(g(x)=(x-4)^2+1\text{.}\) The graph of \(y=f(x)\) has its vertex at the point \((0,0)\text{.}\) Now we will compare this with the graph of \(y=g(x)\) on the same axes.

the graph of two identical parabolas that open upward; one has a vertex at (0,0) and the other one is shifted to the right by 4 units and up by one unit so it's vertex is at (4,1)

Both graphs open upward and have the same shape. Notice that the graph of \(g\) is the same as the graph of \(f\) but is shifted to the right by \(4\) units and up by \(1\) units because its vertex is \((4,1)\text{.}\)

Figure12.1.18The graph of \(f\) and \(g\)

Let's look at another graph. Let \(h(x)=x^2\) and let \(j(x)=-(x+3)^2+4\text{.}\)

the graph of two identical parabolas that open downward; one has a vertex at (0,0) and the other is shifted to the left by 3 units and up by 4 units to have a vertex at (-3,4)

Both parabolas open downward and have the same shape. The graph of \(j\) is the same as the graph of \(h\) but it has been shifted to the left by \(3\) units and up by \(4\) units making its vertex \((-3,4)\text{.}\)

Figure12.1.19The graph of \(h\) and \(j\)

To summarize this, when a quadratic function is written in vertex form, the \(h\)-value is the horizontal shift and the \(k\)-value is the vertical shift.

Now you can try identifying the horizontal and vertical shifts in each function.

Example12.1.20

Identify the horizontal and vertical shifts compared with \(f(x)=x^2\text{.}\)

\(m(x)=(x+7)^2+3\)
\(n(x)=(x-1)^2+6\)
\(o(x)=(x-5)^2-1\)
\(p(x)=(x+3)^2-11\)

Solution

The graph of \(y=m(x)\) is the same as \(y=f(x)\) shifted to the left \(7\) units and up \(3\) units.
The graph of \(y=n(x)\) is the same as \(y=f(x)\) shifted to the right \(1\) unit and up \(6\) units.
The graph of \(y=o(x)\) is the same as \(y=f(x)\) shifted to the right \(5\) units and down \(1\) unit.
The graph of \(y=p(x)\) is the same as \(y=f(x)\) shifted to the left \(3\) units and down \(11\) units.

Subsection12.1.4The Factored Form of a Parabola

There is another form of a parabola, called factored form, which we will explore next. Lets consider the two functions \(q(x)=-x^2+3x+4\) and \(s(x)=-(x-4)(x+1)\text{.}\) Using graphing technology, we will graph \(y=q(x)\) and \(y=s(x)\) on the same axes.

the graph of two identical parabolas that open downward and overlap each other completely — Figure12.1.21Graph of \(q\) and \(s\)

These graphs coincide because the functions are equivalent. We can tell by multiplying out the formula for \(g\) to get back to the formula for \(f\text{.}\)

\begin{align*} g(x)\amp=-(x-4)(x+1)\\ g(x)\amp=-(x^2-3x-4)\\ g(x)\amp=-x^2+3x+4 \end{align*}

Now we can see that \(f\) and \(g\) are really the same function.

Factored form is very useful because we can read the \(x\)-intercepts directly from the function, which in this case are \((4,0)\) and \((-1,0)\text{.}\) We find these by looking for the values that make the factors equal to \(0\text{,}\) so the \(x\)-values have the opposite signs as are shown in the formula. To demonstrate this, we will find the roots by solving \(g(x)=0\text{.}\)

\begin{align*} g(x)\amp=-(x-4)(x+1)\\ \substitute{0}\amp=-(x-4)(x+1) \end{align*}

\begin{align*} x-4\amp=0\amp\text{or}\amp\amp x+1\amp=0\\ x\amp=4\amp\text{or}\amp\amp x\amp=-1 \end{align*}

This shows us that the \(x\)-intercepts are \((4,0)\) and \((-1,0)\text{.}\)

The \(x\)-values of the \(x\)-intercepts are also called zeros or roots. The zeros or roots of the function \(g\) are \(-1\) and \(4\text{.}\)

Fact12.1.22Factored Form of a Quadratic Function

A quadratic function with horizontal intercepts at \((m,0)\) and \((n,0)\) is given by \(f(x)=a(x-m)(x-n)\text{.}\)

Now you can try identifying the horizontal intercepts from each factored form.

Example12.1.23

Write the horizontal intercepts of each function.

\(t(x)=-(x+2)(x-4)\)
\(u(x)=6(x-7)(x-5)\)
\(v(x)=-2(x+1)(x+4)\)
\(w(x)=10(x-8)(x+3)\)

Solution

The horizontal intercepts of \(t\) are \((-2,0)\) and \((4,0)\text{.}\)
The horizontal intercepts of \(u\) are \((7,0)\) and \((5,0)\text{.}\)
The horizontal intercepts of \(v\) are \((-1,0)\) and \((-4,0)\text{.}\)
The horizontal intercepts of \(w\) are \((8,0)\) and \((-3,0)\text{.}\)

Let's summarize the three forms of a quadratic function:

Standard Form: \(f(x)=ax^2+bx+c\text{,}\) with \(y\)-intercept \((0,c)\text{.}\)
Vertex Form: \(f(x)=a(x-h)^2+k\text{,}\) with vertex \((h,k)\text{.}\)
Factored Form: \(f(x)=a(x-m)(x-n)\text{,}\) with \(x\)-intercepts \((m,0)\) and \((n,0)\text{.}\)

SubsectionExercises

Use technology to make a table.

1

Use technology to make a table of values for the function \(F\) defined by \(F(x)={x^{2}-4x+1}\text{.}\)

\(x\)	\(F(x)\)

2

Use technology to make a table of values for the function \(F\) defined by \(F(x)={x^{2}+x-2}\text{.}\)

\(x\)	\(F(x)\)

3

Use technology to make a table of values for the function \(G\) defined by \(G(x)={-x^{2}-x+2}\text{.}\)

\(x\)	\(G(x)\)

4

Use technology to make a table of values for the function \(H\) defined by \(H(x)={-x^{2}+4x-2}\text{.}\)

\(x\)	\(H(x)\)

5

Use technology to make a table of values for the function \(K\) defined by \(K(x)={2x^{2}+2x-5}\text{.}\)

\(x\)	\(K(x)\)

6

Use technology to make a table of values for the function \(K\) defined by \(K(x)={-2x^{2}+3x+1}\text{.}\)

\(x\)	\(K(x)\)

7

Use technology to make a table of values for the function \(f\) defined by \(f(x)={-3x^{2}+7x+27}\text{.}\)

\(x\)	\(f(x)\)

8

Use technology to make a table of values for the function \(g\) defined by \(g(x)={-3x^{2}-6x+37}\text{.}\)

\(x\)	\(g(x)\)

Use technology to make a graph.

9

Use technology to make a graph of \(f\) where \(f(x)=x^2+3x-2\text{.}\)

10

Use technology to make a graph of \(f\) where \(f(x)=x^2-2x-1\text{.}\)

11

Use technology to make a graph of \(f\) where \(f(x)=-x^2+3x+2\text{.}\)

12

Use technology to make a graph of \(f\) where \(f(x)=-x^2+x+2\text{.}\)

13

Use technology to make a graph of \(f\) where \(f(x)=3x^2-6x-5\text{.}\)

14

Use technology to make a graph of \(f\) where \(f(x)=-3x^2-8x+3\text{.}\)

15

Use technology to make a graph of \(f\) where \(f(x)=-3x^2+4x+49\text{.}\)

16

Use technology to make a graph of \(f\) where \(f(x)=2x^2-2x+41\text{.}\)

Use technology to find features of a quadratic function and its graph.

17

Let \(h(x)={-x^{2}+x+4}\text{.}\) Use technology to find the following.

The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .
The domain of \(h\) is .
The range of \(h\) is .
Calculate \(h(1)\text{.}\) .
Solve \(h(x)=-6\text{.}\)
Solve \(h(x)\geq-6\text{.}\)

18

Let \(F(x)={2x^{2}+4x+1}\text{.}\) Use technology to find the following.

The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .
The domain of \(F\) is .
The range of \(F\) is .
Calculate \(F(1)\text{.}\) .
Solve \(F(x)=9\text{.}\)
Solve \(F(x)\leq9\text{.}\)

19

Let \(F(x)={-0.4x^{2}-4.4x-2.6}\text{.}\) Use technology to find the following.

The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .
The domain of \(F\) is .
The range of \(F\) is .
Calculate \(F(-2)\text{.}\) .
Solve \(F(x)=5\text{.}\)
Solve \(F(x)>5\text{.}\)

20

Let \(G(x)={-1.8x^{2}+3.9x-4.6}\text{.}\) Use technology to find the following.

The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .
The domain of \(G\) is .
The range of \(G\) is .
Calculate \(G(1)\text{.}\) .
Solve \(G(x)=-12\text{.}\)
Solve \(G(x)>-12\text{.}\)

21

Let \(H(x)={\frac{x^{2}}{4}+0.1x+5}\text{.}\) Use technology to find the following.

The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .
The domain of \(H\) is .
The range of \(H\) is .
Calculate \(H(5)\text{.}\) .
Solve \(H(x)=8\text{.}\)
Solve \(H(x)>8\text{.}\)

22

Let \(K(x)={\frac{x^{2}}{4}+1.8x-0.1}\text{.}\) Use technology to find the following.

The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .
The domain of \(K\) is .
The range of \(K\) is .
Calculate \(K(-1)\text{.}\) .
Solve \(K(x)=3\text{.}\)
Solve \(K(x)>3\text{.}\)

Use technology to solve quadratic application exercises.

23

An object was launched from the top of a hill with an upward vertical velocity of \(200\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+200t+100}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Find the answer using graphing technology.

The object’s height was feet when it was launched.

24

An object was launched from the top of a hill with an upward vertical velocity of \(60\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+60t+300}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Find the answer using graphing technology.

Use a table to list the object’s height within the first second after it was launched, at an increment of \(0.1\) second. Fill in the blanks. Round your answers to two decimal places when needed.

Time in Seconds	Height in Feet
\(0.1\)
\(0.2\)
\(0.3\)

25

An object was launched from the top of a hill with an upward vertical velocity of \(80\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+80t+200}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Use technology to find the answer.

The object was feet in the air \(5\) seconds after it was launched.

26

An object was launched from the top of a hill with an upward vertical velocity of \(100\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+100t+100}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Find the answer using technology.

seconds after its launch, the object reached its maximum height of feet.

27

An object was launched from the top of a hill with an upward vertical velocity of \(110\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+110t+250}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Find the answer using technology.

seconds after its launch, the object fell to the ground at sea level.

28

An object was launched from the top of a hill with an upward vertical velocity of \(130\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+130t+200}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Find the answer using technology. Round your answers to two decimal places. If there is more than one answer, use a comma to separate them.

The object was \(247\) feet high at the following number of seconds after it was launched: .

29

In a race, a car drove through the starting line at the speed of \(3\) meters per second. It was accelerating at \(3.6\) meters per second squared. Its distance from the starting position can be modeled by the function \(d(t)={1.8t^{2}+3t}\text{.}\) Find the answer using technology.

After seconds, the car was \({394.8}\) meters away from the starting position.

30

In a race, a car drove through the starting line at the speed of \(8\) meters per second. It was accelerating at \(4.1\) meters per second squared. Its distance from the starting position can be modeled by the function \(d(t)={2.05t^{2}+8t}\text{.}\) Find the answer using technology.

After seconds, the car was \({980}\) meters away from the starting position.

31

A farmer purchased \(720\) meters of fencing, and will build a rectangular pen with it. To enclose the largest possible area, what should the pen’s length and width be? Model the pen’s area with a function, and then find its maximum value.

Use a comma to separate your answers.

To enclose the largest possible area, the pen’s length and width should be meters.

32

A farmer purchased \(310\) meters of fencing, and will build a rectangular pen along a river. This implies the pen has only \(3\) fenced sides. To enclose the largest possible area, what should the pen’s length and width be? Model the pen’s area with a function, and then find its maximum value.

To enclose the largest possible area, the pen’s length and width should be meters.

Quadratic Functions in Vertex Form

33

Find the vertex of the graph of

\begin{equation*} y=-9\!\left(x-4\right)^{2}-5 \end{equation*}

34

Find the vertex of the graph of

\begin{equation*} y=-6\!\left(x+3\right)^{2}+3 \end{equation*}

35

Find the vertex of the graph of

\begin{equation*} y=-4\!\left(x-10\right)^{2}-9 \end{equation*}

36

Find the vertex of the graph of

\begin{equation*} y=-2\!\left(x-3\right)^{2}+2 \end{equation*}

37

Find the vertex of the graph of

\begin{equation*} y=0.7\!\left(x+4.1\right)^{2}+8.2 \end{equation*}

38

Find the vertex of the graph of

\begin{equation*} y=3\!\left(x-9.1\right)^{2}-3.6 \end{equation*}

39

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((2,5)\) and has leading coefficient \(a=5\text{.}\)

\(\displaystyle{ f(x) =}\)

40

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((-5,-7)\) and has leading coefficient \(a=7\text{.}\)

\(\displaystyle{ f(x) =}\)

41

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((8,1)\) and has leading coefficient \(a=9\text{.}\)

\(\displaystyle{ f(x) =}\)

42

Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((1,9)\) and has leading coefficient \(a=-8\text{.}\)

\(\displaystyle{ f(x) =}\)

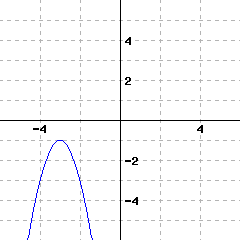
43

A graph of a function \(f\) is given. Use the graph to write a formula for \(f\) in vertex form. You will need to identify the vertex and also one more point on the graph to find the leading coefficient \(a\text{.}\)

\(\displaystyle{ f(x) =}\)

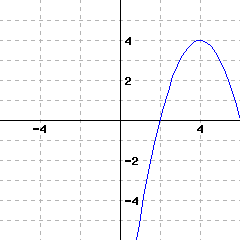
44

\(\displaystyle{ f(x) =}\)

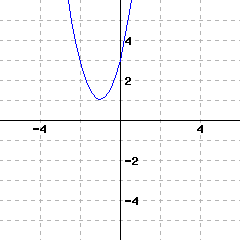
45

\(\displaystyle{ f(x) =}\)

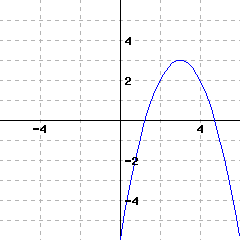
46

\(\displaystyle{ f(x) =}\)

47

Let \(G\) be defined by \(G(x)={\left(x-6\right)^{2}-8}\text{.}\)

What is the domain of \(G\text{?}\)
What is the range of \(G\text{?}\)

48

Let \(H\) be defined by \(H(x)={\left(x+4\right)^{2}-7}\text{.}\)

What is the domain of \(H\text{?}\)
What is the range of \(H\text{?}\)

49

Let \(K\) be defined by \(K(x)={1.3\!\left(x-8\right)^{2}-9}\text{.}\)

What is the domain of \(K\text{?}\)
What is the range of \(K\text{?}\)

50

Let \(K\) be defined by \(K(x)={7.7\!\left(x+3\right)^{2}+4}\text{.}\)

What is the domain of \(K\text{?}\)
What is the range of \(K\text{?}\)

51

Let \(f\) be defined by \(f(x)={-\left(x-5\right)^{2}-1}\text{.}\)

What is the domain of \(f\text{?}\)
What is the range of \(f\text{?}\)

52

Let \(g\) be defined by \(g(x)={-8\!\left(x+6\right)^{2}-6}\text{.}\)

What is the domain of \(g\text{?}\)
What is the range of \(g\text{?}\)

53

Let \(h\) be defined by \(h(x)={7\!\left(x-\left(-1\right)\right)^{2}+\left(-1\right)}\text{.}\)

What is the domain of \(h\text{?}\)
What is the range of \(h\text{?}\)

54

Let \(h\) be defined by \(h(x)={5\!\left(x + {\frac{2}{9}}\right)^{2}+{\frac{1}{6}}}\text{.}\)

What is the domain of \(h\text{?}\)
What is the range of \(h\text{?}\)

55

Let \(F\) be defined by \(F(x)={-2\!\left(x-{\frac{1}{3}}\right)^{2} - {\frac{8}{5}}}\text{.}\)

What is the domain of \(F\text{?}\)
What is the range of \(F\text{?}\)

56

Let \(G\) be defined by \(G(x)={7\!\left(x-{\frac{8}{9}}\right)^{2}+{\frac{1}{3}}}\text{.}\)

What is the domain of \(G\text{?}\)
What is the range of \(G\text{?}\)