1
Find the perimeter and area of the rectangle.
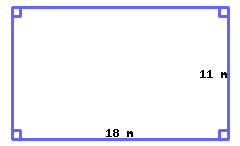
Its perimeter is and its area is .
Perimeter and Area
Find the perimeter and area of the rectangle.

Its perimeter is and its area is .
Find the perimeter and area of a rectangular table top with a length of \({4.1\ {\rm ft}}\) and a width of \({28\ {\rm in}}\text{.}\)
Its perimeter is and its area is .
Find the perimeter and area of the square.

The square’s perimeter is .
The square’s area is .
Find the perimeter and area of the parallelogram.
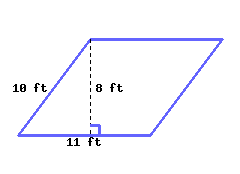
Its perimeter is and its area is .
Find the perimeter and area of the triangle.
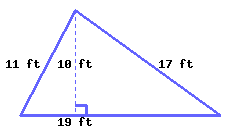
Its perimeter is and its area is .
Find the perimeter and area of the right triangle.
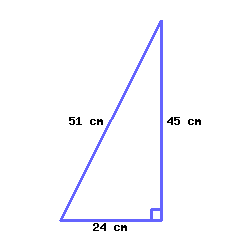
Its perimeter is and its area is .
Find the perimeter and area of the triangle.
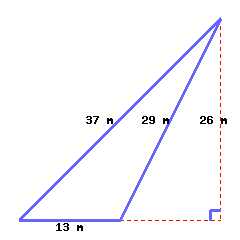
Its perimeter is and its area is .
Find the area of a triangular flag with a base of \({3.5\ {\rm m}}\) and a height of \({70\ {\rm cm}}\text{.}\)
Its area is .
Find the area of the traepzoid.
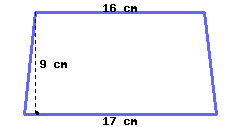
Its area is .
A circle’s radius is \({10\ {\rm m}}\text{.}\)
This circle’s circumference, in terms of \(\pi\text{,}\) is .
This circle’s circumference, rounded to the hundredth place, is .
This circle’s area, in terms of \(\pi\text{,}\) is .
This circle’s area, rounded to the hundredth place, is .
A circle’s diameter is \({4\ {\rm m}}\text{.}\)
This circle’s circumference, in terms of \(\pi\text{,}\) is .
This circle’s circumference, rounded to the hundredth place, is .
This circle’s area, in terms of \(\pi\text{,}\) is .
This circle’s area, rounded to the hundredth place, is .
Find the perimeter and area of this shape.
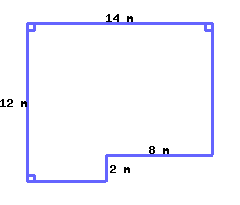
Its perimeter is and its area is .
Find the perimeter and area of this polygon.
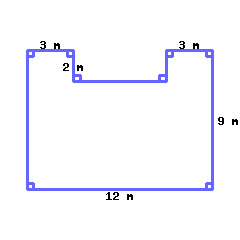
Its perimeter is and its area is .
Find the perimeter and area of this polygon.
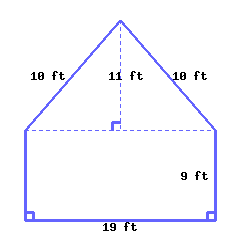
Its perimeter is and its area is .
Find the perimeter and area of this shape, which is a semicircle on top of a rectangle.
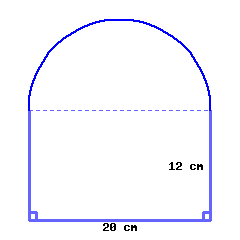
Use decimals in your answers. Don’t leave \(\pi\) as it is.
Its perimeter is and its area is .
Volume
Find the volume of this rectangular prism.
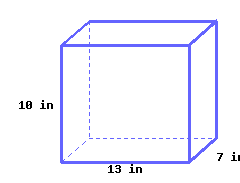
Its volume is .
A cube’s side length is \({8\ {\rm cm}}\text{.}\) Its volume is .
A shoe box’s base is \({1.9\ {\rm ft}}\) by \({9\ {\rm in}}\text{,}\) and its height is \({4.5\ {\rm in}}\text{.}\) Find the shoe box’s volume.
Its volume is .
A cylinder’s base’s radius is \({5\ {\rm m}}\text{,}\) and its height is \({10\ {\rm m}}\text{.}\)
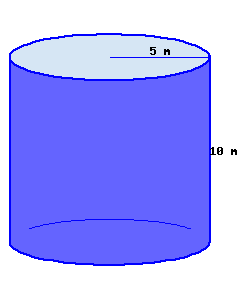
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
A cylinder’s base’s diameter is \({4\ {\rm ft}}\text{,}\) and its height is \({2\ {\rm ft}}\text{.}\)
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
There is a cylindrical tube used to hold scrolls. Its radius is \({6\ {\rm cm}}\text{,}\) and its height is \({1.3\ {\rm m}}\text{.}\) Find the tube’s volume.
Its volume is .