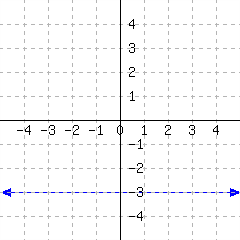ORCCA Horizontal, Vertical, Parallel, and Perpendicular Lines

Section 3.8 Horizontal, Vertical, Parallel, and Perpendicular Lines

Objectives: PCC Course Content and Outcome Guide

MTH 60 CCOG 4.4
MTH 60 CCOG 5.3
MTH 60 CCOG 6.7
MTH 60 CCOG 7.5

Figure 3.8.1. Alternative Video Lessons

The equations of horizontal and vertical lines distinguish them from other line equations enough to merit a special investigation. In addition, pairs of lines that are parallel or perpendicular to each other have interesting features and properties. This section examines the geometric features of these types of lines.

the graph of a horizontal line passing through the point (0,3) — Figure 3.8.2. Horizontal Line

the graph of a vertical line passing through the point (3,0) — Figure 3.8.3. Vertical Line

the graph of two parallel slanted lines — Figure 3.8.4. Two Parallel Lines

the graph of a slanted line and the line that crosses it at a 90 degree angle — Figure 3.8.5. Two Perpendicular Lines

Subsection 3.8.1 Horizontal Lines and Vertical Lines

We learned in Section 3.7 that all lines can be written in standard form (3.7.1). When either $A$ or $B$ equal $0\text{,}$ we end up with a horizontal or vertical line, as we will soon see. Let's take the standard form line equation, $Ax+Bx=C\text{,}$ and one at a time let $A=0$ and $B=0$ and simplify each equation.

\begin{align*} Ax+By\amp=C\amp Ax+By\amp=C\\ \substitute{0}x+By\amp=C\amp Ax+\substitute{0}y\amp=C\\ By\amp=C\amp Ax\amp=C\\ y\amp=\divideunder{C}{B}\amp x\amp=\divideunder{C}{A}\\ y\amp=k\amp x\amp=h \end{align*}

At the end we just renamed the constant numbers $\frac{C}{B}$ and $\frac{C}{A}$ to $k$ and $h$ because of tradition. What is important, is that you view $h$ and $k$ (as well as $A\text{,}$ $B\text{,}$ and $C$) as constants: numbers that have some specific value and don't change in the context of one problem.

Think about one of these equations: $y=k\text{.}$ It says that the $y$-value is the same no matter where you are on the line. If you wanted to plot points on this line, you are free to move far to the left or far to the right on the $x$-axis, but then you always move up (or down) to make the $y$-value equal $k\text{.}$ What does such a line look like?

Example 3.8.6.

Let's plot the line with equation $y=3\text{.}$ (Note that this is the same as $0x+1y=3\text{.}$) To plot some points, it doesn't matter what $x$-values we use. All that matters is that $y$ is always $3\text{.}$

a horizontal line at y=3 — Figure 3.8.7. $y=3$

A line like this is horizontal, parallel to the horizontal axis. All lines with an equation in the form

\begin{equation*} y=k \end{equation*}

(or, in standard form, $0x+By=C$) are horizontal.

Example 3.8.8.

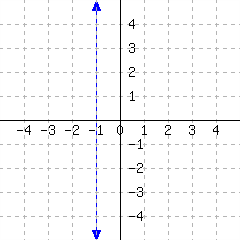
Let's plot the line with equation $x=5\text{.}$ Points on the line always have $x=5\text{,}$ so if we wanted to make a table for plotting points, we are required to make all of the $x$-values be $5\text{.}$ From there, we have complete freedom to let $y$ take any value. Here we take some random $y$-values.

$x$	$y$
$5$	$-6$
$5$	$-2$
$5$	$1$
$5$	$5$

These points are plotted in Figure 3.8.9.

a vertical line at x=5 — Figure 3.8.9. $x=5$

Note that the equation for this line is the same as $x+0y=5\text{.}$ An alternative for making a table is to choose our $y$-values first and substitute them into the equation.

$y$	$x+0y=5\implies x=5$	Ordered Pair
$-6$	$x+0(-6)=5\implies x=5$	$(5,-6)$
$-2$	$x+0(-2)=5\implies x=5$	$(5,-2)$
$1$	$x+0(1)=5\implies x=5$	$(5,1)$
$5$	$x+0(5)=5\implies x=5$	$(5,5)$

In each case no matter what value $y$ is, we find that the equation tells us that $x=5\text{.}$

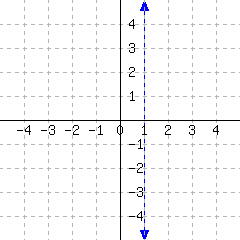
A line like this is vertical, parallel to the vertical axis. All lines with an equation in the form

\begin{equation*} x=h \end{equation*}

(or, in standard form, $Ax+0y=C$) are vertical.

Example 3.8.10. Zero Slope.

In Checkpoint 3.4.17, we learned that a horizontal line's slope is $0\text{,}$ because the distance doesn't change as time moves on. So the numerator in the slope formula (3.4.3) is $0\text{.}$ Now, if we know a line's slope and its $y$-intercept, we can use slope-intercept form (3.5.1) to write its equation:

\begin{align*} y\amp=mx+b\\ y\amp=0x+b\\ y\amp=b \end{align*}

This provides us with an alternative way to think about equations of horizontal lines. They have a certain $y$-intercept $b\text{,}$ and they have slope $0\text{.}$

We use horizontal lines to model scenarios where there is no change in $y$-values, like when Kato stopped for $12$ hours (he deserved a rest)!

Checkpoint 3.8.11. Plotting Points.

Example 3.8.12. Slope of a Vertical Line.

What is the slope of a vertical line? Figure 3.8.13 shows three lines passing through the origin, each steeper than the last. In each graph, you can see a slope triangle that uses a “run” of $1$ unit.

a line with a slope of 1/1=1 — Figure 3.8.13.

a line with a slope of 2/1=2, which is steeper than the first line — Figure 3.8.13.

If we continued making the line steeper and steeper until it was vertical, the slope triangle would still have a “run” of $1\text{,}$ but the “rise” would become larger and larger with no upper limit. The slope would be $m=\frac{\text{very large}}{1}\text{.}$ Actually if the line is vertical, the “rise” segment we've drawn, will never intercept the line. So the slope of a vertical line can be thought of as “infinitely large.” We usually say that the slope of a vertical line is undefined. Some people say that a vertical line has no slope.

Fact 3.8.14.

The slope of a vertical line is undefined.

Remark 3.8.15.

Be careful not to mix up “no slope” (which means “its slope is undefined”) with “has slope $0\text{.}$” If a line has slope $0\text{,}$ it does have a slope.

If you are familiar with NBA basketball, some players wear number $0\text{.}$ That's not the same thing as “not having a number”. This is similar to the situation with having slope $0$ versus not having slope.

Checkpoint 3.8.16. Plotting Points.

Example 3.8.17.

Let $x$ represent the price of a new $60$-inch television at Target on Black Friday (which was $\$650$), and let $y$ be the number of hours you will watch something on this TV over its lifetime. What is the relationship between $x$ and $y\text{?}$

Well, there is no getting around the fact that $x=650\text{.}$ As for $y\text{,}$ without any extra information about your viewing habits, it could theoretically be as low as $0$ or it could be anything larger than that. If we graph this scenario, we have to graph the equation $x=650$ which we now know to give a vertical line, and we get Figure 3.8.18.

eps pdf png svg tex

Figure 3.8.18. New TV: hours watched versus purchase price; negative $y$-values omitted since they make no sense in context

Horizontal Lines	Vertical Lines
A line is horizontal if and only if its equation can be written \begin{equation} y=k \end{equation} for some constant $k\text{.}$	A line is vertical if and only if its equation can be written \begin{equation} x=h \end{equation} for some constant $h\text{.}$
In standard form (3.7.1), any line with equation \begin{equation} 0x+By=C \end{equation} is horizontal.	In standard form (3.7.1), any line with equation \begin{equation} Ax+0y=C \end{equation} is vertical.
If the line with equation $y=k$ is horizontal, it has a $y$-intercept at $(0,k)$ and has slope $0\text{.}$	If the line with equation $x=h$ is vertical, it has an $x$-intercept at $(h,0)$ and its slope is undefined. Some say it has no slope, and some say the slope is infinitely large.
In the slope-intercept form (3.5.1), any line with equation \begin{equation} y=0x+b \end{equation} is horizontal.	It's impossible to write the equation of a vertical line in slope-intercept form (3.5.1), because vertical lines do not have a defined slope.

Figure 3.8.19. Summary of Horizontal and Vertical Line Equations

Subsection 3.8.2 Parallel Lines

Example 3.8.20.

Two trees were planted in the same year, and their growth over time is modeled by the two lines in Figure 3.8.21. Use linear equations to model each tree's growth, and interpret their meanings in this context.

We can see Tree 1's equation is $y=\frac{2}{3}x+2\text{,}$ and Tree 2's equation is $y=\frac{2}{3}x+5\text{.}$ Tree 1 was $2$ feet tall when it was planted, and Tree 2 was $5$ feet tall when it was planted. Both trees have been growing at the same rate, $\frac{2}{3}$ feet per year, or $2$ feet every $3$ years.

This is a Cartesian grid with two parallel lines. Tree 1 has a slope triangle from (0,2) to (3,4) for a slope of 2/3. Tree 2 has a slope triangle from (0,5) to (3.7) for a slope of 2/3. — Figure 3.8.21. Two Trees' Growth Chart

An important observation right now is that those two lines are parallel. Why? For lines with positive slopes, the bigger a line's slope, the steeper the line is slanted. As a result, if two lines have the same slope, they are slanted at the same angle, thus they are parallel.

Fact 3.8.22.

Any two vertical lines are parallel to each other. For two non-vertical lines, they are parallel if and only if they have the same slope.

Checkpoint 3.8.23.

Checkpoint 3.8.24.

Subsection 3.8.3 Perpendicular Lines

The slopes of two perpendicular lines have a special relationship too.

Figure 3.8.25 walks you through an explanation of this relationship.

the graph of two perpendicular lines, where one has a slope of m — (a) Two generic perpendicular lines, where one has slope $m\text{.}$

the previous graph with a slope triangle added; the rise is m and the run is 1 — (a) Two generic perpendicular lines, where one has slope $m\text{.}$

The second line in Figure 3.8.25 has slope

\begin{equation*} \frac{\Delta y}{\Delta x}=\frac{-1}{m}=-\frac{1}{m}\text{.} \end{equation*}

Fact 3.8.26.

A vertical line and a horizontal line are perpendicular. For two lines that are neither vertical nor horizontal, they are perpendicular if and only if the slope of one is the negative reciprocal of the slope of the other. That is, if one has slope $m\text{,}$ the other has slope $-\frac{1}{m}\text{.}$

Another way to say this is that the product of the slopes of two perpendicular lines is $-1$ (assuming both of the lines have a slope in the first place). That is, if there are two perpendicular lines and we let $m_1$ and $m_2$ represent their slopes, then $m_1\cdot m_2=-1\text{.}$

Not convinced? Here are three pairs of perpendicular lines where we can see if the pattern holds.

the graph of lines y=2x-2 and y=-1/2x+2 showing that they are perpendicular lines. — Figure 3.8.27. Graphing $y=2x-2$ and $y=-\frac{1}{2}x+2\text{.}$ Note the relationship between their slopes: $2=-\frac{1}{-\sfrac{1}{2}}$

the graph of lines y=-3x+4 and y=1/3x-3 showing that they are perpendicular. — Figure 3.8.28. Graphing $y=-3x+4$ and $y=\frac{1}{3}x-3\text{.}$ Note the relationship between their slopes: $-3=-\frac{1}{\sfrac{1}{3}}$

the graph of lines y=x and y=-x showing that they are perpendicular — Figure 3.8.29. Graphing $y=x$ and $y=-x\text{.}$ Note the relationship between their slopes: $1=-\frac{1}{-1}$

Example 3.8.30.

Line $A$ passes through $(-2,10)$ and $(3,-10)\text{.}$ Line $B$ passes through $(-4,-4)$ and $(8,-1)\text{.}$ Determine whether these two lines are parallel, perpendicular or neither.

Explanation

We will use the slope formula to find both lines' slopes:

\begin{align*} \text{Line }A\text{'s slope}\amp=\frac{y_2-y_1}{x_2-x_1}\amp\text{Line }B\text{'s slope}\amp=\frac{y_2-y_1}{x_2-x_1}\\ \amp=\frac{-10-10}{3-(-2)}\amp\amp=\frac{-1-(-4)}{8-(-4)}\\ \amp=\frac{-20}{5}\amp\amp=\frac{3}{12}\\ \amp=-4\amp\amp=\frac{1}{4} \end{align*}

Their slopes are not the same, so those two lines are not parallel.

The product of their slopes is $(-4)\cdot\frac{1}{4}=-1\text{,}$ which means the two lines are perpendicular.

Checkpoint 3.8.31.

Reading Questions 3.8.4 Reading Questions

1.

Explain the difference between a line that has no slope and a line that has slope $0\text{.}$

2.

If you make a table of $x$- and $y$-values for either a horizontal line or a vertical line, what is going to happen in one of the two columns?

3.

If you know two points on one line, and you know two points on a second line, what could you do to determine whether or not the two lines are perpendicular?

Exercises 3.8.5 Exercises

Review and Warmup

1.

Evaluate the following expressions. If the answer is undefined, you may answer with DNE (meaning “does not exist”).

$\displaystyle{ \frac{7}{0} = }$
$\displaystyle{ \frac{0}{7} = }$

2.

Evaluate the following expressions. If the answer is undefined, you may answer with DNE (meaning “does not exist”).

$\displaystyle{ \frac{0}{8} = }$
$\displaystyle{ \frac{8}{0} = }$

3.

A line passes through the points $(5,8)$ and $(-3,8)\text{.}$ Find this line’s slope.

4.

A line passes through the points $(3,10)$ and $(-1,10)\text{.}$ Find this line’s slope.

5.

A line passes through the points $(-8,-5)$ and $(-8,3)\text{.}$ Find this line’s slope.

6.

A line passes through the points $(-6,-1)$ and $(-6,5)\text{.}$ Find this line’s slope.

7.

Consider the equation:

\begin{equation*} y=1 \end{equation*}

Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.

$(4,1)$
$(-4,1)$
$(0,7)$
$(1,4)$

8.

Consider the equation:

\begin{equation*} y=1 \end{equation*}

Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.

$(-6,1)$
$(5,1)$
$(0,9)$
$(1,2)$

9.

Consider the equation:

\begin{equation*} x+1=0 \end{equation*}

Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.

$(-1,0)$
$(-1,3)$
$(0,-6)$
$(1,-1)$

10.

Consider the equation:

\begin{equation*} x+1=0 \end{equation*}

Which of the following ordered pairs are solutions to the given equation? There may be more than one correct answer.

$(1,-1)$
$(-1,0)$
$(0,-8)$
$(-1,4)$

Tables for Horizontal and Vertical Lines

11.

Fill out this table for the equation $y=8\text{.}$ The first row is an example.

$x$	$y$	Points
$-3$	$8$	$\left(-3,8\right)$
$-2$
$-1$
$0$
$1$
$2$

12.

Fill out this table for the equation $y=9\text{.}$ The first row is an example.

$x$	$y$	Points
$-3$	$9$	$\left(-3,9\right)$
$-2$
$-1$
$0$
$1$
$2$

13.

Fill out this table for the equation $x=-1\text{.}$ The first row is an example.

$x$	$y$	Points
$-1$	$-3$	$\left(-1,-3\right)$
	$-2$
	$-1$
	$0$
	$1$
	$2$

14.

Fill out this table for the equation $x=-9\text{.}$ The first row is an example.

$x$	$y$	Points
$-9$	$-3$	$\left(-9,-3\right)$
	$-2$
	$-1$
	$0$
	$1$
	$2$

Line Equations

15.

A line’s graph is shown. Write an equation for the line.

eps pdf png svg tex

16.

A line’s graph is shown. Write an equation for the line.

eps pdf png svg tex

17.

A line’s graph is shown. Write an equation for the line.

eps pdf png svg tex

18.

A line’s graph is shown. Write an equation for the line.

eps pdf png svg tex

19.

A line passes through the points $(-2,3)$ and $(-3,3)\text{.}$ Find an equation for this line.

An equation for this line is .

20.

A line passes through the points $(5,6)$ and $(2,6)\text{.}$ Find an equation for this line.

An equation for this line is .

21.

A line passes through the points $(8,1)$ and $(8,-5)\text{.}$ Find an equation for this line.

An equation for this line is .

22.

A line passes through the points $(10,-3)$ and $(10,0)\text{.}$ Find an equation for this line.

An equation for this line is .

Intercepts

23.

Find the $y$-intercept and $x$-intercept of the line given by the equation. If a particular intercept does not exist, enter none into all the answer blanks for that row.

\begin{equation*} x = -8 \end{equation*}

	$x$-value	$y$-value	Location
$y$-intercept
$x$-intercept

24.

Find the $y$-intercept and $x$-intercept of the line given by the equation. If a particular intercept does not exist, enter none into all the answer blanks for that row.

\begin{equation*} x = -6 \end{equation*}

	$x$-value	$y$-value	Location
$y$-intercept
$x$-intercept

25.

Find the $y$-intercept and $x$-intercept of the line given by the equation. If a particular intercept does not exist, enter none into all the answer blanks for that row.

\begin{equation*} y = -4 \end{equation*}

	$x$-value	$y$-value	Location
$y$-intercept
$x$-intercept

26.

Find the $y$-intercept and $x$-intercept of the line given by the equation. If a particular intercept does not exist, enter none into all the answer blanks for that row.

\begin{equation*} y = -1 \end{equation*}

	$x$-value	$y$-value	Location
$y$-intercept
$x$-intercept

Graphs of Horizontal and Vertical Lines

27.

Graph the line $y=1\text{.}$

28.

Graph the line $y+5=0\text{.}$

29.

Graph the line $x=2\text{.}$

30.

Graph the line $x-3=0\text{.}$

Parallel or Perpendicular?

31.

Line $m$ passes points $(1,3)$ and $(-3,-9)\text{.}$

Line $n$ passes points $(5,20)$ and $(4,17)\text{.}$

These two lines are

parallel
perpendicular
neither parallel nor perpendicular

32.

Line $m$ passes points $(-21,28)$ and $(-7,16)\text{.}$

Line $n$ passes points $(-35,33)$ and $(7,-3)\text{.}$

These two linea are

parallel
perpendicular
neither parallel nor perpendicular

33.

Line $m$ passes points $(-5,8)$ and $(5,6)\text{.}$

Line $n$ passes points $(-4,-16)$ and $(2,14)\text{.}$

These two lines are

parallel
perpendicular
neither parallel nor perpendicular

34.

Line $m$ passes points $(-5,15)$ and $(5,-1)\text{.}$

Line $n$ passes points $(-16,0)$ and $(-24,-5)\text{.}$

These two lines are

parallel
perpendicular
neither parallel nor perpendicular

35.

Line $m$ passes points $(-3,-5)$ and $(-4,-4)\text{.}$

Line $n$ passes points $(-2,-9)$ and $(1,3)\text{.}$

These two lines are

parallel
perpendicular
neither parallel nor perpendicular

36.

Line $m$ passes points $(6,-8)$ and $(4,-8)\text{.}$

Line $n$ passes points $(3,7)$ and $(10,7)\text{.}$

These two lines are

parallel
perpendicular
neither parallel nor perpendicular

37.

Line $m$ passes points $(-6,-2)$ and $(-6,-9)\text{.}$

Line $n$ passes points $(1,3)$ and $(1,-1)\text{.}$

These two lines are

parallel
perpendicular
neither parallel nor perpendicular

38.

Line $m$ passes points $(-4,-9)$ and $(-4,0)\text{.}$

Line $n$ passes points $(3,10)$ and $(3,1)\text{.}$

These two lines are

parallel
perpendicular
neither parallel nor perpendicular

Parallel and Perpendicular Line Equations

39.

A line passes through the point $(9,5)\text{,}$ and it’s parallel to the line $y=-2\text{.}$ Find an equation for this line.

40.

A line passes through the point $(-3,-2)\text{,}$ and it’s parallel to the line $y=1\text{.}$ Find an equation for this line.

41.

A line passes through the point $(-10,5)\text{,}$ and it’s parallel to the line $x=3\text{.}$ Find an equation for this line.

42.

A line passes through the point $(4,-7)\text{,}$ and it’s parallel to the line $x=5\text{.}$ Find an equation for this line.

43.

Line $k$ has the equation $y={4x-2}\text{.}$

Line $\ell$ is parallel to line $k\text{,}$ but passes through the point $(4,{18})\text{.}$

Find an equation for line $\ell$ in both point-slope form and slope-intercept form.

An equation for $\ell$ in point-slope form is: .

An equation for $\ell$ in slope-intercept form is: .

44.

Line $k$ has the equation $y={5x+5}\text{.}$

Line $\ell$ is parallel to line $k\text{,}$ but passes through the point $(1,{-5})\text{.}$

Find an equation for line $\ell$ in both point-slope form and slope-intercept form.

An equation for $\ell$ in point-slope form is: .

An equation for $\ell$ in slope-intercept form is: .

45.

Line $k$ has the equation $y={-{\frac{1}{7}}x-3}\text{.}$

Line $\ell$ is parallel to line $k\text{,}$ but passes through the point $(-2,{-{\frac{5}{7}}})\text{.}$

Find an equation for line $\ell$ in both point-slope form and slope-intercept form.

An equation for $\ell$ in point-slope form is: .

An equation for $\ell$ in slope-intercept form is: .

46.

Line $k$ has the equation $y={-{\frac{2}{9}}x+10}\text{.}$

Line $\ell$ is parallel to line $k\text{,}$ but passes through the point $(3,{-{\frac{11}{3}}})\text{.}$

Find an equation for line $\ell$ in both point-slope form and slope-intercept form.

An equation for $\ell$ in point-slope form is: .

An equation for $\ell$ in slope-intercept form is: .

47.

Line $k$ has the equation $y={-x+9}\text{.}$

Line $\ell$ is perpendicular to line $k\text{,}$ and passes through the point $(-1,{-4})\text{.}$

Find an equation for line $\ell\text{.}$

48.

Line $k$ has the equation $y={4x+2}\text{.}$

Line $\ell$ is perpendicular to line $k$ and passes through the point $(2,{{\frac{9}{2}}})\text{.}$

Find an equation for line $\ell$ in both point-slope form and slope-intercept form.

An equation for $\ell$ in point-slope form is: .

An equation for $\ell$ in slope-intercept form is: .

49.

Line $k$’s equation is $y={-{\frac{6}{5}}x-3}\text{.}$

Line $\ell$ is perpendicular to line $k$ and passes through the point $(2,{{\frac{14}{3}}})\text{.}$

Find an equation for line $\ell$ in both point-slope form and slope-intercept form.

An equation for $\ell$ in point-slope form is: .

An equation for $\ell$ in slope-intercept form is: .

50.

Line $k$ has the equation ${x-9y}=-45\text{.}$

Line $\ell$ is perpendicular to line $k$ and passes through the point $(1,{-8})\text{.}$

Find an equation for line $\ell$ in both point-slope form and slope-intercept form.

An equation for $\ell$ in point-slope form is: .

An equation for $\ell$ in slope-intercept form is: .

Challenge

51.

Prove that a triangle with vertices at the points $(1, 1)\text{,}$ $(-4, 4)\text{,}$ and $(-3, 0)$ is a right triangle.

\(x\)	\(y\)
\(5\)	\(-6\)
\(5\)	\(-2\)
\(5\)	\(1\)
\(5\)	\(5\)

\(y\)	\(x+0y=5\implies x=5\)	Ordered Pair
\(-6\)	\(x+0(-6)=5\implies x=5\)	\((5,-6)\)
\(-2\)	\(x+0(-2)=5\implies x=5\)	\((5,-2)\)
\(1\)	\(x+0(1)=5\implies x=5\)	\((5,1)\)
\(5\)	\(x+0(5)=5\implies x=5\)	\((5,5)\)

Horizontal Lines	Vertical Lines
A line is horizontal if and only if its equation can be written \begin{equation} y=k \end{equation} for some constant \(k\text{.}\)	A line is vertical if and only if its equation can be written \begin{equation} x=h \end{equation} for some constant \(h\text{.}\)
In standard form (3.7.1), any line with equation \begin{equation} 0x+By=C \end{equation} is horizontal.	In standard form (3.7.1), any line with equation \begin{equation} Ax+0y=C \end{equation} is vertical.
If the line with equation \(y=k\) is horizontal, it has a \(y\)-intercept at \((0,k)\) and has slope \(0\text{.}\)	If the line with equation \(x=h\) is vertical, it has an \(x\)-intercept at \((h,0)\) and its slope is undefined. Some say it has no slope, and some say the slope is infinitely large.
In the slope-intercept form (3.5.1), any line with equation \begin{equation} y=0x+b \end{equation} is horizontal.	It's impossible to write the equation of a vertical line in slope-intercept form (3.5.1), because vertical lines do not have a defined slope.

\(x\)	\(y\)	Points
\(-3\)	\(8\)	\(\left(-3,8\right)\)
\(-2\)
\(-1\)
\(0\)
\(1\)
\(2\)

\(x\)	\(y\)	Points
\(-3\)	\(9\)	\(\left(-3,9\right)\)
\(-2\)
\(-1\)
\(0\)
\(1\)
\(2\)