Skip to main content

Section 8.4 Geometry Applications

Alternative Video Lesson.

Subsection 8.4.1 Solving Equations for Geometry Problems

With geometry problems in algebra, it is really helpful to draw a picture to understand the scenario better. After drawing the shape and labeling the given information, we will choose the formula to use from the list in Subsection 8.3.3.

Example 8.4.1.

An Olympic-size swimming pool is rectangular and 50 m in length. We don't know its width, but we do know that it required 150 m of painter's tape to outline the edge of the pool during recent renovations. Use this information to set up an equation and find the width of the pool.

Explanation

The pool's shape is a rectangle, so it helps to sketch a rectangle representing the pool as in Figure 8.4.2. Since we know its length is 50 m, it is a good idea to label that in the sketch. The width is our unknown quantity, so we can use \(w\) as a variable to represent the pool's width in meters and label that too.

epspdfpngsvgtex
Figure 8.4.2. An Olympic-size pool

Since it required 150 m of painter's tape to outline the pool, we know the perimeter of the pool is 150 m. This suggests using the perimeter formula for a rectangle: \(P=2(\ell+w)\text{.}\) (This formula was discussed in Subsection 8.3.1).

With this formula, we can substitute \(150\) in for \(P\) and \(50\) in for \(\ell\text{:}\)

\begin{equation*} 150=2(50+w). \end{equation*}

Now we can solve the equation for the width of the pool.

First, we will distribute on the right side, and then isolate \(w\text{.}\)

\begin{align*} 150\amp=100+2w\\ 150\subtractright{100}\amp=100\subtractright{100}+2w\\ 50\amp=2w\\ \divideunder{50}{2}\amp=\divideunder{2w}{2}\\ 25\amp=w\text{.} \end{align*}

Checking the solution \(w=25\) meters:

\begin{align*} 150\amp=2(50+w)\\ 150\amp\stackrel{?}{=}2(50+\substitute{25})\\ 150\amp\stackrel{?}{=}2(75)\\ 150\amp\stackrel{\checkmark}{=}150\text{.} \end{align*}

We found that the width of the pool is \(25\) meters.

Checkpoint 8.4.3.

Let's look at another example. In this one we need to use an algebraic expression for one of the sides of a rectangle.

Example 8.4.4.

Azul is designing a rectangular garden and they have \(40\) meters of wood planking for the border. Their garden's length is \(4\) meters less than three times the width, and the perimeter must be \(40\) meters. Find the garden's length and width.

Explanation

Let Azul's garden width be \(w\) meters. We can then represent the length as \(3w-4\) meters since we are told that it is \(4\) meters less than three times the width. It's given that the perimeter is \(40\) meters. Substituting those values into the formula, we have:

\begin{align*} P\amp=2(\ell+w)\\ 40\amp=2(3w-4+w)\\ 40\amp=2(4w-4)\amp\text{Like terms were combined.} \end{align*}

The next step to solve this equation is to remove the parentheses by distribution.

\begin{align*} 40\amp=2(4w-4)\\ 40\amp=8w-8\\ 40\addright{8}\amp=8w-8\addright{8}\\ 48\amp=8w\\ \divideunder{48}{8}\amp=\divideunder{8w}{8}\\ 6\amp=w\text{.} \end{align*}

Checking the solution \(w=6\text{:}\)

\begin{align*} 40\amp=2(4w-4)\\ 40\amp\stackrel{?}{=}2(4(\substitute{6})-4)\\ 40\amp\stackrel{\checkmark}{=}2(20)\text{.} \end{align*}

To determine the length, recall that this was represented by \(3w-4\text{,}\) which is:

\begin{align*} 3w-4\amp=3(\substitute{6})-4\\ \amp=14\text{.} \end{align*}

Thus, the width of Azul's garden is \(6\) meters and the length is \(14\) meters.

Checkpoint 8.4.5.

For triangle problems, we may need to use the Pythagorean Theorem that we learned in Subsection 7.1.2. If we know the lengths of two sides of a right triangle then we can find the length of the third side.

Example 8.4.6.

Tan owns a road sign manufacturing company and he is producing triangular yield signs for the State of Oregon. The signs are equilateral triangles measuring \(36\) inches on each side as shown in Figure 8.4.7. Find the area of one sign in square feet to help Tan estimate the amount of material he needs to produce the signs.

Explanation

We will start by converting \(36\) inches to \(3\) feet, because the area needs to be in square feet. The area of a triangle is found using \(A=\frac{1}{2}bh\text{,}\) where \(A\) is the area, \(b\) is the width of the base, and \(h\) is the height. In this case the base is at the top of the triangle.

We know the width of the triangle is \(3\) feet, but we don't know the height. By drawing in the height we form two right triangles so we can use the Pythagorean Theorem to find the height. Half of the width is \(1.5\) feet, so we will substitute for \(b\) and \(c\) in the pythagorean theorem.

According to Pythagorean Theorem, we have:

\begin{align*} c^2\amp=a^2+b^2\\ 3^2\amp=a^2+1.5^2\\ 9\amp=a^2+2.25\\ 9\subtractright{2.25}\amp=a^2+2.25\subtractright{2.25}\\ 6.75\amp=a^2\\ \sqrt{6.75}\amp=a\\ 2.598\amp\approx a \end{align*}

The height of the triangle is approximately \(2.598\) feet.

a yield sign that is an equilateral triangle; There is a vertical line down the middle cutting it into two right triangles; each side of the triangle is 36 inches; the height is labeled a
epspdfpngsvgtex
Figure 8.4.7.

Now we can calculate the area of one sign.

\begin{align*} A\amp=\frac{1}{2}bh\\ \amp\approx\frac{1}{2}(3)(\substitute{2.598})\\ \amp=3.897 \end{align*}

The area of one sign is approximately 3.897 ft2.

Now we will look at an example that involves a circle. It can be difficult to measure the radius of a circle or cylinder. But if we can measure the circumference, then we can find the radius.

Example 8.4.8.

Batula wants to order a custom replacement column for the front of her house and she needs to know the radius. She takes a string and wraps it around the old column. She measures the string and finds the circumference is \(3\) feet, \(2.5\) inches. What is the radius of the column?

Explanation

The formula for the circumference of a circle is \(C=2\pi r\text{,}\) where \(C\) stands for the circumference and \(r\) stands for the radius.

We will let the radius of Batula's column be \(r\) inches. It's given that the circumference is \(3\) feet, \(2.5\) inches, so let's convert \(3\) feet into inches.

\begin{align*} 3\,\text{ft}\amp=\frac{3\,\text{ft}}{1}\cdot\frac{12\,\text{in}}{1\,\text{ft}}\\ \amp=\frac{3\,\cancel{\text{ft}}}{1}\cdot\frac{12\,\text{in}}{1\,\cancel{\text{ft}}}\\ \amp=3\cdot12\,\text{in}\\ \amp=36\,\text{in} \end{align*}

Since \(3\) feet is \(36\) inches, we can add the \(2.5\) inches for a total of \(38.5\) inches. Substituting the circumference into the formula, we have:

\begin{align*} C\amp=2\pi r\\ 38.5\amp=2\pi r \end{align*}

The next step is to divide both sides by \(2\pi\text{.}\)

\begin{align*} 38.5\amp=2\pi r\\ \divideunder{38.5}{2\pi}\amp=\divideunder{2\pi r}{2\pi}\\ 6.127\amp\approx r\text{.} \end{align*}

Checking the solution \(r\approx6.13\) inches:

\begin{align*} 38.5\amp=2\pi r\\ 38.5\amp\stackrel{?}{\approx}2\pi(\substitute{6.127})\\ 38.5\amp\stackrel{\checkmark}{\approx}38.5\text{.} \end{align*}

Therefore, Batula should order a column with a radius of \(6.127\) inches. A specific measurement like that may not be possible, but Batula could round to something like \(6\,\frac{1}{8}\) inches, which is very close. If the manufacturer wanted the diameter instead, we would multiply that by \(2\) to get \(12.25\) or \(6\,\frac{1}{4}\) inches.

Here is an example using volume.

Example 8.4.9.

Mark is designing a cylindrical container for his ice cream business. He wants each container to be \(15\) centimeters tall and hold \(1\) gallon of ice cream. What dimension should Mark use for the radius of the container?

Explanation

The formula for the volume of a cylinder is \(V=\pi r^2h\text{,}\) where \(V\) stands for the volume, \(r\) stands for the radius and \(h\) is the height.

Since the volume is in gallons and the dimensions are in centimeters, we need to convert \(1\) gallon to cubic centimeters.

\begin{align*} 1\,\text{gal}\amp=\frac{1\,\text{gal}}{1}\cdot\frac{231\,\text{in}^3}{1\,\text{gal}}\cdot\frac{2.54^3\,\text{cm}^3}{1\,\text{in}^3}\\ \amp=\frac{1\,\cancel{\text{gal}}}{1}\cdot\frac{231\,\cancel{\text{in}^3}}{1\,\cancel{\text{gal}}}\cdot\frac{2.54^3\,\text{cm}^3}{1\,\cancel{\text{in}^3}}\\ \amp=1\cdot231\cdot2.54^3\,\text{cm}^3\\ \amp=3785.41\,\text{cm}^3 \end{align*}

Now we can substitute the volume and height into the formula:

\begin{align*} V\amp=\pi r^2h\\ 3785.41\amp=\pi r^2(15) \end{align*}

The next step is to divide both sides by \(15\pi\text{.}\)

\begin{align*} 3785.41\amp=15\pi r^2\\ \divideunder{3785.41}{15\pi}\amp=\divideunder{15\pi r^2}{15\pi}\\ \frac{3785.41}{15\pi}\amp=r^2\\ \sqrt{\frac{3785.41}{15\pi}}\amp=r\\ 8.963\amp\approx r\text{.} \end{align*}

Checking the solution \(r\approx8.963\) centimeters:

\begin{align*} 3785.41\amp=\pi r^2h\\ 3785.41\amp\stackrel{?}{\approx}\pi(\substitute{8.963}^2)(15)\\ 3785.41\amp\stackrel{\checkmark}{\approx}3783.18\text{.} \end{align*}

Note that our check is approximate because we rounded our answer. Mark will want to make the radius of his container at least \(8.963\) centimeters. He should make it a little larger to have space at the top of the container.

Subsection 8.4.2 Proportionality in Similar Triangles

Another appliction of geometry involves similar triangles. Two triangles are considered similar if they have the same angles and their side lengths are proportional, as shown in Figure 8.4.10:

Figure 8.4.10. Similar Triangles

In the first triangle in Figure 8.4.10, the ratio of the left side length to the hypotenuse length is \(\frac{1\,\text{cm}}{2\,\text{cm}}\text{;}\) in the second triangle, the ratio of the left side length to the hypotenuse length is \(\frac{3\,\text{cm}}{6\,\text{cm}}\text{.}\) Since both reduce to \(\frac{1}{2}\text{,}\) we can write the following proportion:

\begin{equation*} \frac{1\,\text{cm}}{2\,\text{cm}}=\frac{3\,\text{cm}}{6\,\text{cm}} \end{equation*}

If we extend this concept, we can use it to solve for an unknown side length. Consider the two similar triangles in the next example.

Example 8.4.11.
Figure 8.4.12. Similar Triangles

Since the two triangles are similar, we know that their side length should be proportional. To determine the unknown length, we can set up a proportion and solve for \(x\text{:}\)

\begin{align*} \frac{\text{bigger triangle's left side length in cm}}{\text{bigger triangle's bottom side length in cm}}\amp=\frac{\text{smaller triangle's left side length in cm}}{\text{smaller triangle's bottom side length in cm}}\\ \frac{x\,\text{cm}}{6\,\text{cm}}\amp=\frac{3\,\text{cm}}{4\,\text{cm}}\\ \frac{x}{6}\amp=\frac{3}{4}\\ \multiplyleft{6}\frac{x}{6}\amp=\multiplyleft{6}\frac{3}{4}\\ x\amp=\frac{18}{4}\\ x\amp=\frac{9}{2}=4.5 \end{align*}

The unknown side length is then 4.5 cm.

Remark 8.4.13.

Looking at the triangles in Figure 8.4.10, you may notice that there are many different proportions you could set up, such as:

\begin{align*} \frac{2\,\text{cm}}{1\,\text{cm}}\amp=\frac{6\,\text{cm}}{3\,\text{cm}}\\ \frac{2\,\text{cm}}{6\,\text{cm}}\amp=\frac{1\,\text{cm}}{3\,\text{cm}}\\ \frac{6\,\text{cm}}{2\,\text{cm}}\amp=\frac{3\,\text{cm}}{1\,\text{cm}}\\ \frac{3\sqrt{3}\,\text{cm}}{\sqrt{3}\,\text{cm}}\amp=\frac{3\,\text{cm}}{1\,\text{cm}} \end{align*}

This is often the case when we set up ratios and proportions.

If we take a second look at Figure 8.4.12, there are also several other proportions we could have used to find the value of \(x\text{.}\)

\begin{align*} \frac{\text{bigger triangle's left side length}}{\text{smaller triangle's left side length}}\amp=\frac{\text{bigger triangle's bottom side length}}{\text{smaller triangle's bottom side length}}\\ \\ \frac{\text{smaller triangle's bottom side length}}{\text{bigger triangle's bottom side length}}\amp=\frac{\text{smaller triangle's left side length}}{\text{bigger triangle's left side length}}\\ \\ \frac{\text{bigger triangle's bottom side length}}{\text{smaller triangle's bottom side length}}\amp=\frac{\text{bigger triangle's left side length} }{\text{smaller triangle's left side length}} \end{align*}

Written as algebraic proportions, these three equations would, respectively, be

\begin{align*} \frac{x\,\text{cm}}{3\,\text{cm}}\amp= \frac{6\,\text{cm}}{4\,\text{cm}}, \amp \frac{4\,\text{cm}}{6\,\text{cm}}\amp= \frac{3\,\text{cm}}{x\,\text{cm}}, \amp \frac{6\,\text{cm}}{4\,\text{cm}}\amp= \frac{x\,\text{cm}}{3\,\text{cm}} \end{align*}

While these are only a few of the possibilities, if we clear the denominators from any properly designed proportion, every one is equivalent to \(x=4.5\text{.}\)

Exercises 8.4.3 Exercises

1.

A circle’s circumference is \({4\pi\ {\rm mm}}\text{.}\)

  1. This circle’s diameter is .

  2. This circle’s radius is .

2.

A circle’s circumference is \({6\pi\ {\rm mm}}\text{.}\)

  1. This circle’s diameter is .

  2. This circle’s radius is .

3.

A circle’s circumference is \({36\ {\rm cm}}\text{.}\) Find the following values. Round your answer to at least 2 decimal places.

  1. This circle’s diameter is .

  2. This circle’s radius is .

4.

A circle’s circumference is \({38\ {\rm cm}}\text{.}\) Find the following values. Round your answer to at least 2 decimal places.

  1. This circle’s diameter is .

  2. This circle’s radius is .

5.

A circle’s circumference is \({12\pi\ {\rm mm}}\text{.}\)

  1. This circle’s diameter is .

  2. This circle’s radius is .

6.

A circle’s circumference is \({14\pi\ {\rm mm}}\text{.}\)

  1. This circle’s diameter is .

  2. This circle’s radius is .

7.

A circle’s circumference is \({45\ {\rm cm}}\text{.}\) Find the following values. Round your answer to at least 2 decimal places.

  1. This circle’s diameter is .

  2. This circle’s radius is .

8.

A circle’s circumference is \({47\ {\rm cm}}\text{.}\) Find the following values. Round your answer to at least 2 decimal places.

  1. This circle’s diameter is .

  2. This circle’s radius is .

9.

A cylinder’s base’s radius is \({4\ {\rm m}}\text{,}\) and its volume is \({160\pi\ {\rm m^{3}}}\text{.}\)

This cylinder’s height is .

10.

A cylinder’s base’s radius is \({10\ {\rm m}}\text{,}\) and its volume is \({200\pi\ {\rm m^{3}}}\text{.}\)

This cylinder’s height is .

11.

A rectangle’s area is \({336\ {\rm mm^{2}}}\text{.}\) Its height is \({16\ {\rm mm}}\text{.}\)

Its base is .

12.

A rectangle’s area is \({276\ {\rm mm^{2}}}\text{.}\) Its height is \({12\ {\rm mm}}\text{.}\)

Its base is .

13.

A rectangular prism’s volume is \({13224\ {\rm ft^{3}}}\text{.}\) The prism’s base is a rectangle. The rectangle’s length is \({24\ {\rm ft}}\) and the rectangle’s width is \({19\ {\rm ft}}\text{.}\)

This prism’s height is .

14.

A rectangular prism’s volume is \({5600\ {\rm ft^{3}}}\text{.}\) The prism’s base is a rectangle. The rectangle’s length is \({25\ {\rm ft}}\) and the rectangle’s width is \({16\ {\rm ft}}\text{.}\)

This prism’s height is .

15.

A triangle’s area is \({175.5\ {\rm m^{2}}}\text{.}\) Its base is \({27\ {\rm m}}\text{.}\)

Its height is .

16.

A triangle’s area is \({275.5\ {\rm m^{2}}}\text{.}\) Its base is \({29\ {\rm m}}\text{.}\)

Its height is .

17.

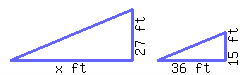
The following two triangles are similar to each other. Find the length of the missing side.

epspdfpngsvgtex

The missing side’s length is

18.

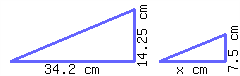
The following two triangles are similar to each other. Find the length of the missing side.

epspdfpngsvgtex

The missing side’s length is

19.

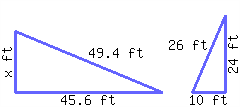
The following two triangles are similar to each other. Find the length of the missing side.

epspdfpngsvgtex

The missing side’s length is

20.

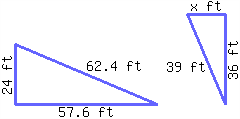
The following two triangles are similar to each other. Find the length of the missing side.

epspdfpngsvgtex

The missing side’s length is

login