Section 8.5 Quantities in the Physical World Chapter Review
¶Subsection 8.5.1 Scientific Notation
In Section 8.1 we covered the definition of scientific notation, how to convert to and from scientific notation, and how to do some calculations in scientific notation.
Example 8.5.1. Scientific Notation for Large Numbers.
The distance to the star Betelgeuse is about \(3{,}780{,}000{,}000{,}000{,}000\) miles. Write this number in scientific notation.
The gross domestic product (GDP) of California in the year 2017 was about \(\$2.746\times10^{13}\text{.}\) Write this number in standard notation.
\(3{,}780{,}000{,}000{,}000{,}000=3.78\times10^{15}\text{.}\)
\(\$2.746\times10^{13}=\$2{,}746{,}000{,}000{,}000\text{.}\)
Example 8.5.2. Scientific Notation for Small Numbers.
Human DNA forms a double helix with diameter \(2\times10^{-9}\) meters. Write this number in standard notation.
A single grain of Forget-me-not (Myosotis) pollen is about \(0.00024\) inches in diameter. Write this number in scientific notation.
\(2\times10^{-9}=0.000000002\text{.}\)
\(0.00024=2.4\times10^{-4}\text{.}\)
Example 8.5.3. Multiplying and Dividing Using Scientific Notation.
The fastest spacecraft so far have traveled about \(5\times10^6\) miles per day.
If that spacecraft traveled at that same speed for \(2\times10^4\) days (which is about \(55\) years), how far would it have gone? Write your answer in scientific notation.
The nearest star to Earth, besides the Sun, is Proxima Centauri, about \(2.5\times10^{13}\) miles from Earth. How many days would you have to fly in that spacecraft at top speed to reach Proxima Centauri
-
Remember that you can find the distance traveled by multiplying the rate of travel times the time traveled: \(d=r\cdot t\text{.}\) So this problem turns into
\begin{align*} d\amp=r\cdot t\\ d\amp=\left(\highlight{5}\times10^6\right)\cdot \left(\highlight{2}\times10^4\right)\\ \end{align*}Multiply coefficient with coefficient and power of \(10\) with power of \(10\text{.}\)
\begin{align*} \amp=\left(\highlight{5}\cdot\highlight{2}\right) \left(10^6\times10^4\right)\\ \amp=\highlight{10}\times10^{10}\\ \end{align*}Remember that this still isn't in scientific notation. So we convert like this:
\begin{align*} \amp=\highlight{1.0\times10^1}\times10^{10}\\ \amp=1.0\times10^{11} \end{align*}So, after traveling for \(2\times10^4\) days (55 years), we will have traveled about \(1.0\times10^{11}\) miles. That's one-hundred million miles. I hope someone remembered the snacks.
-
Since we are looking for time, let's solve the equation \(d=r\cdot t\) for \(t\) by dividing by \(r\) on both sides: \(t=\frac{d}{r}\text{.}\) So we have:
\begin{align*} t\amp=\frac{d}{r}\\ t\amp=\frac{2.5\times10^{13}}{5\times10^6}\\ \end{align*}Now we can divide coefficient by coefficient and power of \(10\) with power of \(10\text{.}\)
\begin{align*} t\amp=\frac{2.5}{5}\times\frac{10^{13}}{10^6}\\ t\amp=\highlight{0.5}\times10^7\\ t\amp=\highlight{5\times10^{-1}}\times10^7\\ t\amp=5\times10^6 \end{align*}This means that to get to Proxima Centauri, even in our fastest spacecraft, would take \(5\times10^6\) years. Converting to standard form, this is \(5{,}000{,}000\) years. I think we're going to need a faster ship.
Subsection 8.5.2 Unit Conversion
Unit conversion is a particular process that uses unit ratios to convert units. You may refer to Appendix B to find unit conversion facts needed to do these conversions.
Example 8.5.4. Using Multiple Unit Ratios.
How many grams are in \(5\) pounds?
So \(5\) pounds is about \(2268\) grams.
Example 8.5.5. Converting Squared or Cubed Units.
Convert \(240\) square inches into square centimeters.
So \(240\) square inches is approximately \(1548\) square centimeters.
Example 8.5.6. Converting Rates.
Gold has a density of 19.3 g⁄mL. What is this density in ounces per cubic inch?
Notice that we did not need to raise any unit ratios to a power since there is a conversion fact that tells us that \(1\,\text{in}^3\approx16.39\,\text{mL}\text{.}\)
Thus, the density of gold is about 11.16 oz⁄in3.
Subsection 8.5.3 Geometry Formulas
In Section 8.3 we established the following formulas.
- Perimeter of a Rectangle
\(P=2(\ell+w)\)
- Area of a Rectangle
\(A=\ell w\)
- Area of a Triangle
\(A=\frac{1}{2}bh\)
- Circumference of a Circle
\(c=2\pi r\)
- Area of a Circle
\(A=\pi r^2\)
- Volume of a Rectangular Prism
\(V=wdh\)
- Volume of a Cylinder
\(V=\pi r^2h\)
- Volume of a Rectangular Prism or Cylinder
\(V=Bh\)
Exercises 8.5.4 Exercises
Scientific Notation
1.
Write the following number in scientific notation.
\(350=\)
2.
Write the following number in scientific notation.
\(450000=\)
3.
Write the following number in scientific notation.
\(0.0055=\)
4.
Write the following number in scientific notation.
\(0.00065=\)
5.
Write the following number in decimal notation without using exponents.
\(7.51\times 10^{4}=\)
6.
Write the following number in decimal notation without using exponents.
\(8.51\times 10^{3}=\)
7.
Write the following number in decimal notation without using exponents.
\(9.5\times 10^{0}=\)
8.
Write the following number in decimal notation without using exponents.
\(1.49\times 10^{0}=\)
9.
Write the following number in decimal notation without using exponents.
\(2.5\times 10^{-3}=\)
10.
Write the following number in decimal notation without using exponents.
\(3.49\times 10^{-4}=\)
11.
Multiply the following numbers, writing your answer in scientific notation.
\((5\times 10^{3})(7\times 10^{2})=\)
12.
Multiply the following numbers, writing your answer in scientific notation.
\((5\times 10^{5})(4\times 10^{5})=\)
13.
Divide the following numbers, writing your answer in scientific notation.
\(\displaystyle\frac{5.4\times 10^{3}}{6\times 10^{-2}}=\)
14.
Divide the following numbers, writing your answer in scientific notation.
\(\displaystyle\frac{4.2\times 10^{4}}{7\times 10^{-2}}=\)
Unit Conversion
15.
Convert \({211\ {\rm tbsp}}\) to teaspoons.
16.
Convert \({5.98\ {\rm t}}\) to kilograms.
17.
Convert \({9.5\ {\rm s}}\) to milliseconds.
18.
Convert \({43\ {\rm hm}}\) to feet.
19.
Convert \({8.9\ {\rm yd}}\) to centimeters.
20.
Convert \({2.7\ {\rm pt}}\) to gallons.
21.
Convert \({48\ {\rm cm^{2}}}\) to square inches.
22.
Convert \({2.08\ {\rm ft^{3}}}\) to cubic miles.
23.
Convert \({52.8\ {\textstyle\frac{\rm\mathstrut dam}{\rm\mathstrut s}}}\) to meters per millisecond.
24.
Convert \({226\ {\textstyle\frac{\rm\mathstrut mi^{2}}{\rm\mathstrut wk}}}\) to acres per day.
25.
Convert \({7.6\ {\textstyle\frac{\rm\mathstrut T}{\rm\mathstrut s}}}\) to pounds per nanosecond.
26.
Convert \({46\ {\textstyle\frac{\rm\mathstrut B}{\rm\mathstrut d}}}\) to kilobytes per week.
27.
Carly’s bedroom has \({107\ {\rm ft^{2}}}\) of floor. She would like to carpet the floor, but carpeting is sold by the square yard. How many square yards of carpeting will she need to get?
28.
Jon is traveling in Europe and renting a car. He is used to thinking of gasoline amounts in gallons, but in Europe it is sold in liters. After filling the gas tank, he notices it took \({32\ {\rm L}}\) of gas. How many gallons is that?
29.
Cody was driving at a steady speed of \({39\ {\rm mph}}\) for \(11\) minutes. How far did he travel in that time?
30.
The algae in a pond is growing at a rate of \({0.3\ {\textstyle\frac{\rm\mathstrut kg}{\rm\mathstrut d}}}\text{.}\) How much algae is in the pond after \(4\) weeks?
Geometry
33.
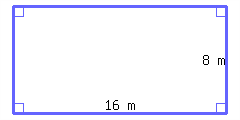
Find the area of the rectangle below.
34.
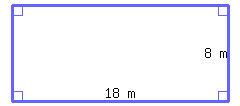
Find the perimeter and area of a rectangular table top with a length of \({5.9\ {\rm ft}}\) and a width of \({32\ {\rm in}}\text{.}\)
Its perimeter is and its area is .
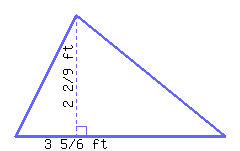
35.
Find the perimeter and area of the triangle.
Its perimeter is and its area is .
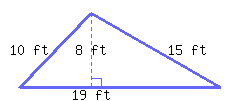
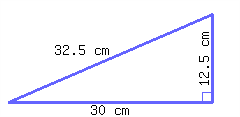
36.
Find the perimeter and area of the right triangle.
Its perimeter is and its area is .
37.
The area of the triangle below is square feet.
38.
Find the area of a triangular flag with a base of \({2.7\ {\rm m}}\) and a height of \({70\ {\rm cm}}\text{.}\)
Its area is .
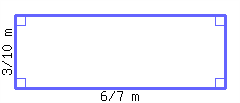
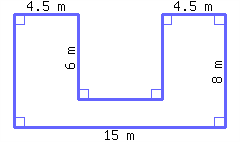
39.
Find the perimeter and area of this shape.
Its perimeter is and its area is .
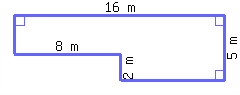
40.
Find the perimeter and area of this polygon.
Its perimeter is and its area is .
41.
The formula \(A=\frac{1}{2}\,r\,n\,s\) gives the area of a regular polygon with side length \(s\text{,}\) number of sides \(n\) and, apothem \(r\text{.}\) (The apothem is the distance from the center of the polygon to one of its sides.)
What is the area of a regular pentagon with \(s= {72\ {\rm in}}\) and \(r={96\ {\rm in}}\text{?}\)
42.
A circle’s radius is \({9\ {\rm m}}\text{.}\)
The circumference, in terms of \(\pi\text{,}\) is .
This circle’s circumference, rounded to the hundredths place, is .
This circle’s area, in terms of \(\pi\text{,}\) is .
This circle’s area, rounded to the hundredths place, is .
43.
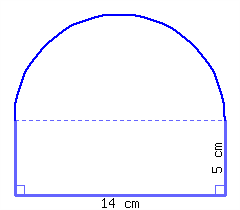
Find the perimeter and area of this shape, which is a semicircle on top of a rectangle.
Its perimeter is and its area is .
44.
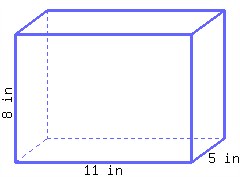
Find the volume of this rectangular prism.
45.
A cube’s side length is \({3\ {\rm cm}}\text{.}\) Its volume is .
46.
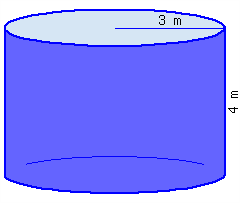
Find the volume of this cylinder.
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredths place, is .
47.
A cylinder’s base’s diameter is \({6\ {\rm ft}}\text{,}\) and its height is \({5\ {\rm ft}}\text{.}\)
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredths place, is .
48.
A cylinder’s base’s diameter is \({18\ {\rm ft}}\text{,}\) and its height is \({6\ {\rm ft}}\text{.}\)
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredths place, is .
49.
Fill out the table with various formulas as they were given in this section.
| Rectangle Perimeter | |
| Rectangle Area | |
| Triangle Area | |
| Circle Circumference | |
| Circle Area | |
| Rectangular Prism Volume | |
| Cylinder Volume | |
| Volume of either Rectangular Prism or Cylinder |
50.
A circle’s circumference is \({16\pi\ {\rm mm}}\text{.}\)
This circle’s diameter is .
This circle’s radius is .
51.
A circle’s circumference is \({47\ {\rm cm}}\text{.}\) Find the following values. Round your answer to at least 2 decimal places.
This circle’s diameter is .
This circle’s radius is .
52.
A circle’s circumference is \({49\ {\rm cm}}\text{.}\) Find the following values. Round your answer to at least 2 decimal places.
This circle’s diameter is .
This circle’s radius is .
53.
A cylinder’s base’s radius is \({2\ {\rm m}}\text{,}\) and its volume is \({8\pi\ {\rm m^{3}}}\text{.}\)
This cylinder’s height is .
54.
A rectangular prism’s volume is \({5355\ {\rm ft^{3}}}\text{.}\) The prism’s base is a rectangle. The rectangle’s length is \({21\ {\rm ft}}\) and the rectangle’s width is \({17\ {\rm ft}}\text{.}\)
This prism’s height is .
55.
A triangle’s area is \({149.5\ {\rm m^{2}}}\text{.}\) Its base is \({23\ {\rm m}}\text{.}\)
Its height is .
56.
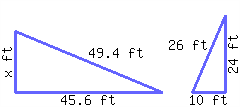
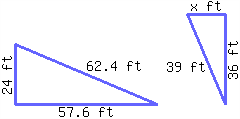
The following two triangles are similar to each other. Find the length of the missing side.
The missing side’s length is
57.
The following two triangles are similar to each other. Find the length of the missing side.
The missing side’s length is