Section 3.1 Cartesian Coordinates
¶Objectives: PCC Course Content and Outcome Guide
When we model a relationship between two variables visually, we use the Cartesian coordinate system. This section covers the basic vocabulary and ideas that come with the Cartesian coordinate system.
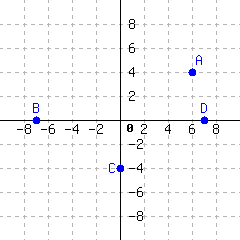
The Cartesian coordinate system identifies the location of every point in a plane. Basically, the system gives every point in a plane its own âaddressâ in relation to a starting point. We'll use a street grid as an analogy. Here is a map with Carl's home at the center. The map also shows some nearby businesses. Assume each unit in the grid represents one city block.
If Carl has an out-of-town guest who asks him how to get to the restaurant, Carl could say:
âFirst go \(2\) blocks east (to the right on the map), then go \(3\) blocks north (up on the map).â
Two numbers are used to locate the restaurant. In the Cartesian coordinate system, these numbers are called coordinates and they are written as the ordered pair \((2,3)\text{.}\) The first coordinate, \(2\text{,}\) represents distance traveled from Carl's house to the east (or to the right horizontally on the graph). The second coordinate, \(3\text{,}\) represents distance to the north (up vertically on the graph).
To travel from Carl's home to the pet shop, he would go \(3\) blocks west, and then \(2\) blocks north.
In the Cartesian coordinate system, the positive directions are to the right horizontally and up vertically. The negative directions are to the left horizontally and down vertically. So the pet shop's Cartesian coordinates are \((-3,2)\text{.}\)
Remark 3.1.5.
It's important to know that the order of Cartesian coordinates is (horizontal, vertical). This idea of communicating horizontal information before vertical information is consistent throughout most of mathematics.
Checkpoint 3.1.6.
Warning 3.1.7. Notation Issue: Coordinates or Interval?
Unfortunately, the notation for an ordered pair looks exactly like interval notation for an open interval. Context will help you understand if \((1,3)\) indicates the point \(1\) unit right of the origin and \(3\) units up, or if \((1,3)\) indicates the interval of all real numbers between \(1\) and \(3\text{.}\)
Traditionally, the variable \(x\) represents numbers on the horizontal axis, so it is called the \(x\)-axis. The variable \(y\) represents numbers on the vertical axis, so it is called the \(y\)-axis. The axes meet at the point \((0,0)\text{,}\) which is called the origin. Every point in the plane is represented by an ordered pair, \((x,y)\text{.}\)
In a Cartesian coordinate system, the map of Carl's neighborhood would look like this:
Definition 3.1.9. Cartesian Coordinate System.
The Cartesian coordinate systemâ2âen.wikipedia.org/wiki/Cartesian_coordinate_system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed (positive/negative) distances to the point from two fixed perpendicular directed lines, measured in the same unit of length. Those two reference lines are called the horizontal axis and vertical axis, and the point where they meet is the origin. The horizontal and vertical axes are often called the \(x\)-axis and \(y\)-axis.
The plane based on the \(x\)-axis and \(y\)-axis is called a coordinate plane. The ordered pair used to locate a point is called the point's coordinates, which consists of an \(x\)-coordinate and a \(y\)-coordinate. For example, the point \((1,2)\text{,}\) has \(x\)-coordinate \(1\text{,}\) and \(y\)-coordinate \(2\text{.}\) The origin has coordinates \((0,0)\text{.}\)
A Cartesian coordinate system is divided into four quadrants, as shown in Figure 3.1.10. The quadrants are traditionally labeled with Roman numerals.
Example 3.1.11.
On paper, sketch a Cartesian coordinate system with units, and then plot the following points: \((3,2),(-5,-1),(0,-3),(4,0)\text{.}\)
Reading Questions Reading Questions
1.
What are the coordinates of the gas station in the map of Carl's neighborhood?
2.
A Cartesian coordinate system has seven âplacesâ within that are worth noting. What are they? (For example, one of them is Quadrant I.)
Exercises Exercises
Identifying Coordinates
1.
Locate each point in the graph:
Write each pointâs position as an ordered pair, like \((1,2)\text{.}\)
| \(A=\) | \(B=\) |
| \(C=\) | \(D=\) |
2.
Locate each point in the graph:
Write each pointâs position as an ordered pair, like \((1,2)\text{.}\)
| \(A=\) | \(B=\) |
| \(C=\) | \(D=\) |
Creating Sketches of Graphs
3.
Sketch the points \((8,2)\text{,}\) \((5,5)\text{,}\) \((-3,0)\text{,}\) and \((2,-6)\) on a Cartesian plane.
4.
Sketch the points \((1,-4)\text{,}\) \((-3,5)\text{,}\) \((0,4)\text{,}\) and \((-2,-6)\) on a Cartesian plane.
5.
Sketch the points \((208,-50)\text{,}\) \((97,112)\text{,}\) \((-29,103)\text{,}\) and \((-80,-172)\) on a Cartesian plane.
6.
Sketch the points \((110,38)\text{,}\) \((-205,52)\text{,}\) \((-52,125)\text{,}\) and \((-172,-80)\) on a Cartesian plane.
7.
Sketch the points \((5.5,2.7)\text{,}\) \((-7.3,2.75)\text{,}\) \(\left(-\frac{10}{3},\frac{1}{2}\right)\text{,}\) and \(\left(-\frac{28}{5},-\frac{29}{4}\right)\) on a Cartesian plane.
8.
Sketch the points \((1.9,-3.3)\text{,}\) \((-5.2,-8.11)\text{,}\) \(\left(\frac{7}{11},\frac{15}{2}\right)\text{,}\) and \(\left(-\frac{16}{3},\frac{19}{5}\right)\) on a Cartesian plane.
9.
Sketch a Cartesian plane and shade the quadrants where the \(x\)-coordinate is negative.
10.
Sketch a Cartesian plane and shade the quadrants where the \(y\)-coordinate is positive.
11.
Sketch a Cartesian plane and shade the quadrants where the \(x\)-coordinate has the same sign as the \(y\)-coordinate.
12.
Sketch a Cartesian plane and shade the quadrants where the \(x\)-coordinate and the \(y\)-coordinate have opposite signs.
Cartesian Plots in Context
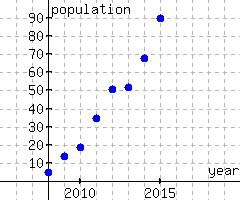
13.
This graph gives the minimum estimates of the wolf population in Washington from 2008 through 2015.
What are the Cartesian coordinates for the point representing the year 2011?
Between 2011 and 2012, the wolf population grew by wolves.
List at least three ordered pairs in the graph.
14.
Here is a graph of the foreign-born US population (in millions) during Census years 1960 to 2010.
What are the Cartesian coordinates for the point representing the year 1980?
Between 1980 and 2000, the US population that is foreign-born increased by million people.
List at least three ordered pairs in the graph.
Regions in the Cartesian Plane
15.
The point \({\left(3,-10\right)}\) is in Quadrant
I
II
III
IV
The point \({\left(-5,7\right)}\) is in Quadrant
I
II
III
IV
The point \({\left(8,9\right)}\) is in Quadrant
I
II
III
IV
The point \({\left(-3,-9\right)}\) is in Quadrant
I
II
III
IV
16.
The point \({\left(6,4\right)}\) is in Quadrant
I
II
III
IV
The point \({\left(4,-5\right)}\) is in Quadrant
I
II
III
IV
The point \({\left(-10,-4\right)}\) is in Quadrant
I
II
III
IV
The point \({\left(-10,4\right)}\) is in Quadrant
I
II
III
IV
17.
Assume the point \((x,y)\) is in Quadrant II, locate the following points:
The point \((-x,y)\) is in Quadrant
I
II
III
IV
The point \((x,-y)\) is in Quadrant
I
II
III
IV
The point \((-x,-y)\) is in Quadrant
I
II
III
IV
18.
Assume the point \((x,y)\) is in Quadrant IV, locate the following points:
The point \((-x,y)\) is in Quadrant
I
II
III
IV
The point \((x,-y)\) is in Quadrant
I
II
III
IV
The point \((-x,-y)\) is in Quadrant
I
II
III
IV
19.
Answer the following questions on the coordinate system:
For the point \((x,y)\text{,}\) if \(x>0 \text{ and } y>0\text{,}\) then the point is in/on
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
the x-axis
the y-axis
For the point \((x,y)\text{,}\) if \(x>0 \text{ and } y\lt 0\text{,}\) then the point is in/on
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
the x-axis
the y-axis
For the point \((x,y)\text{,}\) if \(y=0\text{,}\) then the point is in/on
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
the x-axis
the y-axis
For the point \((x,y)\text{,}\) if \(x\lt 0 \text{ and } y\lt 0\text{,}\) then the point is in/on
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
the x-axis
the y-axis
For the point \((x,y)\text{,}\) if \(x=0\text{,}\) then the point is in/on
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
the x-axis
the y-axis
For the point \((x,y)\text{,}\) if \(x\lt 0 \text{ and } y>0\text{,}\) then the point is in/on
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
the x-axis
the y-axis
Plotting Points and Choosing a Scale
20.
What would be the difficulty with trying to plot \((12,4)\text{,}\) \((13,5)\text{,}\) and \((310,208)\) all on the same graph?
21.
The points \((3,5)\text{,}\) \((5,6)\text{,}\) \((7,7)\text{,}\) and \((9,8)\) all lie on a straight line. What can go wrong if you make a plot of a Cartesian plane with these points marked, and you donât have tick marks that are evenly spaced apart?