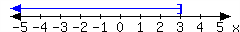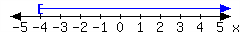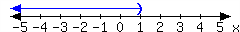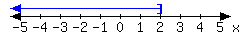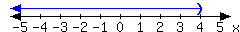ORCCA Variables, Expressions, and Equations Chapter Review

Section 1.9 Variables, Expressions, and Equations Chapter Review

Subsection 1.9.1 Variables and Evaluating Expressions

In Section 1.1 we covered the definitions of variables and expressions, and how to evaluate an expression with a particular number.

Evaluating Expressions.

When we evaluate an expression's value, we substitute each variable with its given value.

Example 1.9.1.

Evaluate the value of $\frac{5}{9}(F - 32)$ if $F=212\text{.}$

\begin{align*} \frac{5}{9}(F - 32)\amp=\frac{5}{9}(212 - 32)\\ \amp=\frac{5}{9}(180)\\ \amp=100 \end{align*}

Substituting a Negative Number.

When we substitute a variable with a negative number, it's important to use parentheses around the number.

Example 1.9.2.

Evaluate the following expressions if $x=-3\text{.}$

$\begin{aligned}[t] x^2\amp=(-3)^2\\ \amp=9 \end{aligned}$
$\begin{aligned}[t] x^3\amp=(-3)^3\\ \amp=(-3)(-3)(-3)\\ \amp=-27 \end{aligned}$
$\begin{aligned}[t] -x^2\amp=-(-3)^2\\ \amp=-9 \end{aligned}$
$\begin{aligned}[t] -x^3\amp=-(-3)^3\\ \amp=-(-27)\\ \amp=27 \end{aligned}$

Subsection 1.9.2 Combining Like Terms

In Section 1.2 we covered the definitions of a term and how to combine like terms.

Example 1.9.3.

List the terms in the expression $5x-3y+\frac{2w}{3}\text{.}$

Explanation

The expression has three terms that are being added, $5x\text{,}$ $-3y$ and $\frac{2w}{3}\text{.}$

Example 1.9.4.

Simplify the expression $5x-3x^2+2x+5x^2\text{,}$ if possible, by combining like terms.

Explanation

This expression has four terms: $5x\text{,}$ $-3x^2\text{,}$ $2x\text{,}$ and $5x^2\text{.}$ Both $5x$ and $2x$ are like terms; also $-3x^2$ and $5x^2$ are like terms. When we combine like terms, we get:

\begin{equation*} 5x-3x^2+2x+5x^2=7x+2x^2 \end{equation*}

Note that we cannot combine $7x$ and $2x^2$ because $x$ and $x^2$ represent different quantities.

Subsection 1.9.3 Comparison Symbols and Notation for Intervals

The following are symbols used to compare numbers.

Symbol	Means	True	True	False
$=$	equals	$13=13$	$\frac{5}{4}=1.25$	$5\stackrel{\text{no}}{=}6$
$\gt$	is greater than	$13\gt11$	$\pi\gt3$	$9\stackrel{\text{no}}{\gt}9$
$\geq$	is greater than or equal to	$13\geq11$	$3\geq3$	$11.2\stackrel{\text{no}}{\geq}10.2$
$\lt$	is less than	$-3\lt8$	$\frac{1}{2}\lt\frac{2}{3}$	$2\stackrel{\text{no}}{\lt}-2$
$\leq$	is less than or equal to	$-3\leq8$	$3\leq3$	$\frac{4}{5}\stackrel{\text{no}}{\leq}\frac{3}{5}$
$\neq$	is not equal to	$10\neq20$	$\frac{1}{2}\neq1.2$	$\frac{3}{8}\stackrel{\text{no}}{\neq}0.375$

Table 1.9.5. Comparison Symbols

The following are some examples of set-builder notation and interval notation.

Graph

Set-builder Notation

Interval Notation

eps pdf png svg tex

$\left\{x\mid x\ge1\right\}$

$[1,\infty)$

eps pdf png svg tex

$\left\{x\mid x\gt1\right\}$

$(1,\infty)$

eps pdf png svg tex

$\left\{x\mid x\le1\right\}$

$(-\infty,1]$

eps pdf png svg tex

$\left\{x\mid x\lt1\right\}$

$(-\infty,1)$

Subsection 1.9.4 Equations and Inequalities as True/False Statements

In Section 1.4 we covered the definitions of an equation and an inequality, as well as how to verify if a particular number is a solution to them.

Checking Possible Solutions.

Given an equation or an inequality (with one variable), checking if some particular number is a solution is just a matter of replacing the value of the variable with the specified number and determining if the resulting equation/inequality is true or false. This may involve some amount of arithmetic simplification.

Example 1.9.6.

Is $-5$ a solution to $2(x+3)-2=4-x\text{?}$

Explanation

To find out, substitute in $-5$ for $x$ and see what happens.

\begin{align*} 2(x+3)-2\amp=4-x\\ 2(\substitute{(-5)}+3)-2\amp\stackrel{?}{=}4-\substitute{(-5)}\\ 2(\highlight{-2})-2\amp\stackrel{?}{=}\highlight{9}\\ \highlight{-4}-2\amp\stackrel{?}{=}9\\ \highlight{-6}\amp\stackrel{\text{no}}{=}9 \end{align*}

So no, $-5$ is not a solution to $2(x+3)-2=4-x\text{.}$

Subsection 1.9.5 Solving One-Step Equations

In Section 1.5 we covered to to add, subtract, multiply, or divide on both sides of an equation to isolate the variable, summarized in Fact 1.5.13. We also learned how to state our answer, either as a solution or a solution set. Last, we discussed how to solve equations with fractions.

Solving One-Step Equations.

When we solve linear equations, we use Properties of Equivalent Equations and follow an algorithm to solve a linear equation.

Example 1.9.7.

Solve for $g$ in $\frac{1}{2}=\frac{2}{3}+g\text{.}$

Explanation

We will subtract $\frac{2}{3}$ on both sides of the equation:

\begin{align*} \frac{1}{2}\amp=\frac{2}{3}+g\\ \frac{1}{2}\subtractright{\frac{2}{3}}\amp=\frac{2}{3}+g\subtractright{\frac{2}{3}}\\ \frac{3}{6}-\frac{4}{6}\amp=g\\ -\frac{1}{6}\amp=g \end{align*}

We will check the solution by substituting $g$ in the original equation with $-\frac{1}{6}\text{:}$

\begin{align*} \frac{1}{2}\amp=\frac{2}{3}+g\\ \frac{1}{2}\amp\stackrel{?}{=}\frac{2}{3}+\left(\substitute{-\frac{1}{6}}\right)\\ \frac{1}{2}\amp\stackrel{?}{=}\frac{4}{6}+\left(-\frac{1}{6}\right)\\ \frac{1}{2}\amp\stackrel{\checkmark}{=}\frac{3}{6} \end{align*}

The solution $-\frac{1}{6}$ is checked and the solution set is $\left\{-\frac{1}{6}\right\}\text{.}$

Subsection 1.9.6 Solving One-Step Inequalities

In Section 1.6 we covered how solving inequalities is very much like how we solve equations, except that if we multiply or divide by a negative we switch the inequality sign.

Solving One-Step Inequalities.

When we solve linear inequalities, we also use Properties of Equivalent Equations with one small complication: When we multiply or divide by the same negative number on both sides of an inequality, the direction reverses!

Example 1.9.8.

Solve the inequality $-2x\geq12\text{.}$ State the solution set with both interval notation and set-builder notation.

Explanation

To solve this inequality, we will divide each side by $-2\text{:}$

\begin{align*} -2x\amp\geq12\\ \divideunder{-2x}{-2}\amp\highlight{{}\leq{}}\divideunder{12}{-2}\amp\amp\text{Note the change in direction.}\\ x\amp\leq-6 \end{align*}

The inequality's solution set in interval notation is $(-\infty,-6]\text{.}$
The inequality's solution set in set-builder notation is $\{x\mid x\leq-6\}\text{.}$

Subsection 1.9.7 Algebraic Properties and Simplifying Expressions

In Section 1.7 we covered the definitions of the identities and inverses, and the various algebraic properties. We then learned about the order of operations.

Example 1.9.9.

Use the associative, commutative, and distributive properties to simplify the expression $5x+9(-2x+3)$ as much as possible.

Explanation

We will remove parentheses by the distributive property, and then combine like terms:

\begin{align*} 5x+9(-2x+3)\amp=5x+9(-2x+3)\\ \amp=5x+9(-2x)+9(3)\\ \amp=5x-18x+27\\ \amp=-13x+27 \end{align*}

Subsection 1.9.8 Modeling with Equations and Inequalities

In Section 1.8 we covered how to translate phrases into mathematics, and how to set up equations and inequalities for application models.

Modeling with Equations and Inequalities.

To set up an equation modeling a real world scenario, the first thing we need to do is to identify what variable we will use. The variable we use will be determined by whatever is unknown in our problem statement. Once we've identified and defined our variable, we'll use the numerical information provided in the equation to set up our equation.

Example 1.9.10.

A bathtub contains 2.5 ft³ of water. More water is being poured in at a rate of 1.75 ft³ per minute. When will the amount of water in the bathtub reach 6.25 ft³?

Explanation

Since the question being asked in this problem starts with “when,” we immediately know that the unknown is time. As the volume of water in the tub is measured in ft³ per minute, we know that time needs to be measured in minutes. We'll defined $t$ to be the number of minutes that water is poured into the tub. Since each minute there are 1.75 ft³ of water added, we will add the expression $1.75t$ to $2.5$ to obtain the total amount of water. Thus the equation we set up is:

\begin{equation*} 2.5+1.75t=6.25 \end{equation*}

Exercises 1.9.9 Exercises

Variables and Evaluating Expressions

1.

Evaluate the expression ${y^{2}}\text{:}$

For $y=8\text{.}$
For $y=-3\text{.}$

2.

Evaluate the expression ${y^{2}}\text{:}$

For $y=5\text{.}$
For $y=-7\text{.}$

3.

Evaluate $\displaystyle{{\frac{2r-9}{9r}}}$ for $r=-9\text{.}$

4.

Evaluate $\displaystyle{{\frac{6r-2}{9r}}}$ for $r=5\text{.}$

5.

Evaluate the expression $\displaystyle \frac{1}{3} \big( x + 4 \big)^2 - 4$ when $x = -7\text{.}$

6.

Evaluate the expression $\displaystyle \frac{1}{4} \big( x + 4 \big)^2 - 2$ when $x = -8\text{.}$

7.

To convert a temperature measured in degrees Fahrenheit to degrees Celsius, there is a formula:

\begin{equation*} C={\frac{5}{9}\!\left(F-32\right)} \end{equation*}

where $C$ represents the temperature in degrees Celsius and $F$ represents the temperature in degrees Fahrenheit.

If a temperature is $5 {^\circ}\text{F}\text{,}$ what is that temperature measured in Celsius?

8.

To convert a temperature measured in degrees Fahrenheit to degrees Celsius, there is a formula:

\begin{equation*} C={\frac{5}{9}\!\left(F-32\right)} \end{equation*}

where $C$ represents the temperature in degrees Celsius and $F$ represents the temperature in degrees Fahrenheit.

If a temperature is $14 {^\circ}\text{F}\text{,}$ what is that temperature measured in Celsius?

9.

The percentage of births in the U.S. delivered via C-section can be given by the following formula for the years since 1996:

\begin{equation*} p = 0.8(y-1996)+21 \end{equation*}

In this formula $y$ is a year after 1996 and $p$ is the percentage of births delivered via C-section for that year.

What percentage of births in the U.S. were delivered via C-section in the year 2001?

of births in the U.S. were delivered via C-section in the year 2001.

10.

The percentage of births in the U.S. delivered via C-section can be given by the following formula for the years since 1996:

\begin{equation*} p = 0.8(y-1996)+21 \end{equation*}

In this formula $y$ is a year after 1996 and $p$ is the percentage of births delivered via C-section for that year.

What percentage of births in the U.S. were delivered via C-section in the year 2003?

of births in the U.S. were delivered via C-section in the year 2003.

Combining Like Terms

11.

Count the number of terms in each expression.

${8t+y+8s^{2}}$
${3t-5x}$
${-5z^{2}+7z}$
${-3y^{2}-3x-5x+2z^{2}}$

12.

Count the number of terms in each expression.

${-9t^{2}+9t^{2}+6z^{2}}$
${2t-9t+5s-1}$
${6x^{2}-7s+x+9y}$
${9t^{2}+8z^{2}}$

13.

List the terms in each expression.

${-6.9t-1.1x+3.4x^{2}}$
${0.7s^{2}+5.3y^{2}-1.5}$
${-3.4x^{2}-2.1t}$
${-7.9s-8.6t^{2}}$

14.

List the terms in each expression.

${-5.2t^{2}+7.1z+1.4t^{2}-0.5s}$
${1.3t-7.7x}$
${-5.6x^{2}+8.5y-8.9x^{2}}$
${-0.1y}$

15.

Simplify each expression, if possible, by combining like terms.

${-{\frac{1}{2}}t-{\frac{3}{7}} - {\frac{9}{2}}t^{2}-t^{2}}$
${-{\frac{5}{3}}s^{2} - {\frac{1}{6}}s^{2}+9z^{2}+{\frac{1}{6}}s}$
${-2t+{\frac{5}{8}}z}$
${-{\frac{3}{7}}y^{2}-2y^{2}+{\frac{6}{7}}}$

16.

Simplify each expression, if possible, by combining like terms.

${{\frac{2}{3}}t^{2}+{\frac{9}{7}}t^{2}}$
${-{\frac{2}{3}}y^{2}+{\frac{7}{6}}s^{2} - {\frac{3}{8}}s^{2}}$
${{\frac{7}{4}}z+s^{2}+{\frac{1}{3}}z^{2}}$
${-9z^{2}+2y^{2}+{\frac{3}{4}}z}$

Comparison Symbols and Notation for Intervals

17.

Decide if each comparison is true or false.

$-{\frac{3}{3}}\neq-{\frac{6}{6}}$
- True
- False
${\frac{29}{4}}\lt{\frac{7}{4}}$
- True
- False
$-{\frac{5}{9}}\lt-{\frac{5}{9}}$
- True
- False
${\frac{7}{4}}\geq-{\frac{58}{7}}$
- True
- False
${\frac{19}{4}}\gt-{\frac{15}{8}}$
- True
- False
${\frac{82}{9}}=-{\frac{41}{5}}$
- True
- False

18.

Decide if each comparison is true or false.

$-{\frac{6}{3}}=-{\frac{12}{6}}$
- True
- False
${\frac{9}{2}}\lt{\frac{9}{2}}$
- True
- False
$-{\frac{16}{3}}\gt{\frac{27}{8}}$
- True
- False
${\frac{11}{6}}\leq-{\frac{6}{4}}$
- True
- False
${\frac{9}{2}}\geq-{\frac{76}{8}}$
- True
- False
${\frac{77}{9}}\neq{\frac{5}{2}}$
- True
- False

19.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

${{\frac{2}{3}}} + {{\frac{4}{5}}}$

${{\frac{4}{3}}} \div {{\frac{1}{4}}}$

20.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

${{\frac{3}{2}}} + {{\frac{1}{3}}}$

${{\frac{4}{5}}} \div {{\frac{4}{5}}}$

21.

For each interval expressed in the number lines, give the interval notation and set-builder notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:
eps pdf png svg tex

In set-builder notation:

In interval notation:
eps pdf png svg tex

In set-builder notation:

In interval notation:

22.

For each interval expressed in the number lines, give the interval notation and set-builder notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:
eps pdf png svg tex

In set-builder notation:

In interval notation:
eps pdf png svg tex

In set-builder notation:

In interval notation:

23.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {{x}} \leq 6 \} }$

24.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {{x}} \leq 8 \} }$

Equations and Inequalities as True/False Statements

25.

Is $-2$ a solution for $x$ in the equation ${-6x-10} = {2x+6}\text{?}$

26.

Is $-10$ a solution for $x$ in the equation ${3x+5} = {2x-4}\text{?}$

27.

Is ${{\frac{3}{4}}}$ a solution for $x$ in the equation ${-{\frac{5}{9}}x - {\frac{1}{2}}} = {-{\frac{67}{54}}}\text{?}$

28.

Is ${6}$ a solution for $y$ in the equation ${{\frac{3}{7}}y+{\frac{1}{6}}} = {{\frac{5}{21}}}\text{?}$

29.

When a plant was purchased, it was $1$ inches tall. It grows $0.6$ inches per day. How many days later will the plant be $12.4$ inches tall?

Assume the plant will be $12.4$ inches tall $d$ days later. We can solve this problem using the equation:

\begin{equation*} 0.6 d+1=12.4 \end{equation*}

Check whether $22$ is a solution for $d$ of this equation.

30.

When a plant was purchased, it was $2.4$ inches tall. It grows $0.7$ inches per day. How many days later will the plant be $11.5$ inches tall?

Assume the plant will be $11.5$ inches tall $d$ days later. We can solve this problem using the equation:

\begin{equation*} 0.7 d+2.4=11.5 \end{equation*}

Check whether $15$ is a solution for $d$ of this equation.

Solving One-Step Equations

31.

Solve the equation.

$\displaystyle{ {r-4}={4} }$

32.

Solve the equation.

$\displaystyle{ {t-10}={-7} }$

33.

Solve the equation.

$\displaystyle{ {{\frac{6}{7}}+p}={-{\frac{5}{8}}} }$

34.

Solve the equation.

$\displaystyle{ {{\frac{6}{5}}+x}={-{\frac{7}{6}}} }$

35.

Solve the equation.

$\displaystyle{ \frac{5}{3}=\frac{x}{27} }$

36.

Solve the equation.

$\displaystyle{ \frac{9}{4}=\frac{x}{28} }$

37.

Solve the equation.

$\displaystyle{ {2y}={16} }$
$\displaystyle{ {2+x}={16} }$

38.

Solve the equation.

$\displaystyle{ {6y}={36} }$
$\displaystyle{ {6+t}={36} }$

39.

Solve the equation.

$\displaystyle{ {54}={-9r} }$
$\displaystyle{ {54}={-9+x} }$

40.

Solve the equation.

$\displaystyle{ {14}={-7r} }$
$\displaystyle{ {14}={-7+x} }$

41.

Solve the equation.

$\displaystyle{ {30} = {-{\frac{10}{7}}m} }$
$\displaystyle{ {-30} = {-{\frac{10}{7}}p} }$

42.

Solve the equation.

$\displaystyle{ {20} = {-{\frac{4}{5}}p} }$
$\displaystyle{ {-20} = {-{\frac{4}{5}}A} }$

Solving One-Step Inequalities

43.

Solve this inequality.

$\displaystyle{ {5} > {x-6} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

44.

Solve this inequality.

$\displaystyle{ {1} > {x-10} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

45.

Solve this inequality.

$\displaystyle{ {2x} \leq {6} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

46.

Solve this inequality.

$\displaystyle{ {3x} \leq {6} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

47.

Solve this inequality.

$\displaystyle{ {-3x} \geq {12} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

48.

Solve this inequality.

$\displaystyle{ {-4x} \geq {12} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

49.

Solve this inequality.

$\displaystyle{ {{\frac{7}{2}}x} > {7} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

50.

Solve this inequality.

$\displaystyle{ {{\frac{8}{7}}x} > {8} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

51.

Solve this inequality.

$\displaystyle{ {-{\frac{9}{5}}x} \leq {9} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

52.

Solve this inequality.

$\displaystyle{ {-{\frac{10}{7}}x} \leq {40} }$

In set-builder notation, the solution set is .

In interval notation, the solution set is .

Algebraic Properties and Simplifying Expressions

53.

What is the additive inverse of $-8\text{?}$

54.

What is the additive inverse of $-6\text{?}$

55.

What is the multiplicative inverse of $-4\text{?}$

56.

What is the multiplicative inverse of $-1\text{?}$

57.

Use the associative property of addition to write an equivalent expression to ${a+\left(19+y\right)}\text{.}$

58.

Use the associative property of addition to write an equivalent expression to ${q+\left(18+p\right)}\text{.}$

59.

Use the associative property of multiplication to write an equivalent expression to ${7\!\left(5m\right)}\text{.}$

60.

Use the associative property of multiplication to write an equivalent expression to ${4\!\left(9p\right)}\text{.}$

61.

Use the commutative property of addition to write an equivalent expression to ${4q+91}\text{.}$

62.

Use the commutative property of addition to write an equivalent expression to ${7y+56}\text{.}$

63.

Use the commutative property of multiplication to write an equivalent expression to ${21r}\text{.}$

64.

Use the commutative property of multiplication to write an equivalent expression to ${87a}\text{.}$

65.

Use the distributive property to write an equivalent expression to ${6\!\left(c+10\right)}$ that has no grouping symbols.

66.

Use the distributive property to write an equivalent expression to ${4\!\left(r+7\right)}$ that has no grouping symbols.

67.

Use the distributive property to simplify ${8-7\!\left(-9-7n\right)}$ completely.

68.

Use the distributive property to simplify ${6-9\!\left(-9-10m\right)}$ completely.

69.

Use the distributive property to simplify ${3p-5p\!\left(7-10p^{2}\right)}$ completely.

70.

Use the distributive property to simplify ${8q-2q\!\left(1-10q^{4}\right)}$ completely.

71.

Fully simplify ${-\left(-5x-4\right)+3\!\left(7x+8\right)}\text{.}$

72.

Fully simplify ${2\!\left(x+8\right)-4\!\left(-x+3\right)}\text{.}$

Modeling with Equations and Inequalities

73.

A bicycle for sale costs ${\$139.36}\text{,}$ which includes $7.2\%$ sales tax. What was the cost before sales tax?

Assume the bicycle’s price before sales tax is $p$ dollars. Write an equation to model this scenario. There is no need to solve it.

74.

A bicycle for sale costs ${\$169.76}\text{,}$ which includes $6.1\%$ sales tax. What was the cost before sales tax?

Assume the bicycle’s price before sales tax is $p$ dollars. Write an equation to model this scenario. There is no need to solve it.

75.

The price of a washing machine after $5\%$ discount is ${\$180.50}\text{.}$ What was the original price of the washing machine (before the discount was applied)?

Assume the washing machine’s price before the discount is $p$ dollars. Write an equation to model this scenario. There is no need to solve it.

76.

The price of a washing machine after $25\%$ discount is ${\$157.50}\text{.}$ What was the original price of the washing machine (before the discount was applied)?

Assume the washing machine’s price before the discount is $p$ dollars. Write an equation to model this scenario. There is no need to solve it.

77.

Lisa is driving an average of $53$ miles per hour, and she is $106$ miles away from home. After how many hours will she reach his home?

Assume Lisa will reach home after $h$ hours. Write an equation to model this scenario. There is no need to solve it.

78.

Emiliano is driving an average of $57$ miles per hour, and he is $228$ miles away from home. After how many hours will he reach his home?

Assume Emiliano will reach home after $h$ hours. Write an equation to model this scenario. There is no need to solve it.