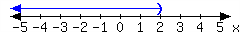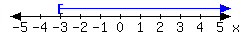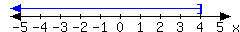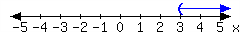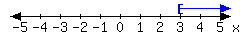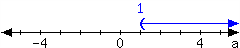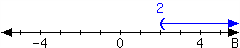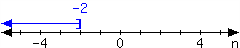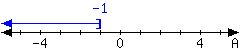ORCCA Comparison Symbols and Notation for Intervals

Skip to main content

$\require{cancel}\require{color}\newcommand{\abs}[1]{\left\lvert#1\right\rvert} \newcommand{\point}[2]{\left(#1,#2\right)} \newcommand{\highlight}[1]{\definecolor{sapphire}{RGB}{59,90,125} {\color{sapphire}{{#1}}}} \newcommand{\firsthighlight}[1]{\definecolor{sapphire}{RGB}{59,90,125} {\color{sapphire}{{#1}}}} \newcommand{\secondhighlight}[1]{\definecolor{emerald}{RGB}{20,97,75} {\color{emerald}{{#1}}}} \newcommand{\unhighlight}[1]{{\color{black}{{#1}}}} \newcommand{\lowlight}[1]{{\color{lightgray}{#1}}} \newcommand{\attention}[1]{\mathord{\overset{\downarrow}{#1}}} \newcommand{\nextoperation}[1]{\mathord{\boxed{#1}}} \newcommand{\substitute}[1]{{\color{blue}{{#1}}}} \newcommand{\pinover}[2]{\overset{\overset{\mathrm{\ #2\ }}{|}}{\strut #1 \strut}} \newcommand{\addright}[1]{{\color{blue}{{{}+#1}}}} \newcommand{\addleft}[1]{{\color{blue}{{#1+{}}}}} \newcommand{\subtractright}[1]{{\color{blue}{{{}-#1}}}} \newcommand{\multiplyright}[2][\cdot]{{\color{blue}{{{}#1#2}}}} \newcommand{\multiplyleft}[2][\cdot]{{\color{blue}{{#2#1{}}}}} \newcommand{\divideunder}[2]{\frac{#1}{{\color{blue}{{#2}}}}} \newcommand{\divideright}[1]{{\color{blue}{{{}\div#1}}}} \newcommand{\negate}[1]{{\color{blue}{{-}}}\left(#1\right)} \newcommand{\cancelhighlight}[1]{\definecolor{sapphire}{RGB}{59,90,125}{\color{sapphire}{{\cancel{#1}}}}} \newcommand{\secondcancelhighlight}[1]{\definecolor{emerald}{RGB}{20,97,75}{\color{emerald}{{\bcancel{#1}}}}} \newcommand{\thirdcancelhighlight}[1]{\definecolor{amethyst}{HTML}{70485b}{\color{amethyst}{{\xcancel{#1}}}}} \newcommand{\apple}{\text{🍎}} \newcommand{\banana}{\text{🍌}} \newcommand{\pear}{\text{🍐}} \newcommand{\cat}{\text{🐱}} \newcommand{\dog}{\text{🐶}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&}$

Section 1.3 Comparison Symbols and Notation for Intervals

Objectives: PCC Course Content and Outcome Guide

MTH 60 CCOG 2.4

As you know, $8$ is larger than $3\text{;}$ that's a specific comparison between two numbers. We can also make a comparison between two less specific numbers, like if we say that average rent in Portland in 2016 is larger than it was in 2009. That makes a comparison using unspecified amounts. In the first half of this section, we will go over the mathematical shorthand notation for making these kinds of comparisons.

In Oregon in 2019, only people who are $18$ years old or older can vote in statewide elections.¹ Does that seem like a statement about the number $18\text{?}$ Maybe. But it's also a statement about numbers like $37$ and $62\text{:}$ it says that people of these ages may vote as well. So the above is actually a statement about a large collection of numbers, not just $18\text{.}$ In the second half of this section, we will get into the mathematical notation for large collections of numbers like this.

Figure 1.3.1. Alternative Video Lesson

Subsection 1.3.1 Comparison Symbols

In everyday language you can say something like “ $8$ is larger than $3\text{.}$ ” In mathematical writing, it's not convenient to write that out in English. Instead the symbol “ $\gt$ ” has been adopted, and it's used like this:

8 > 3

$\begin{equation*} 8\gt3 \end{equation*}$

and read out loud as “ $8$ is greater than $3\text{.}$ ” The symbol “ $\gt$ ” is called the greater-than symbol.

Checkpoint 1.3.2.

Remark 1.3.3.

At some point in history, someone felt that $\gt$ was a good symbol for “is greater than.” In “ $8\gt3\text{,}$ ” the tall side of the symbol is with the larger of the two numbers, and the small pointed side is with the smaller of the two numbers.

Another way to remember how the greater-than symbol works is to imagine the symbol as the open mouth of an alligator, or whatever your favorite animal is. And then remind yourself that the alligator is hungry and it wants to eat the larger number.

We have to be careful when negative numbers are part of the comparison. Is $-8$ larger or smaller than $-3\text{?}$ In some sense $-8$ is larger, because if you owe someone $8$ dollars, that's more than owing them $3$ dollars. But that is not how the $\gt$ symbol works. This symbol is meant to tell you which number is farther to the right on a number line. And if that's how it goes, then $-3$ is larger.

a number line with marks at -8, -3, and 8; text indicates the numbers to the left are lesser numbers, and numbers to the right are greater numbers; text indicates that -3 > -8 and 8 > -3 — How the $\gt$ symbol works.

Checkpoint 1.3.5.

Checkpoint 1.3.6.

The greater-than symbol has a close relative, the greater-than-or-equal-to symbol, “ $\geq\text{.}$ ” It means just like it sounds: the first number is either greater than the second number or equal to it. These are all true statements:

\begin{aligned} 8 & \geq 3 & 3 & \geq - 8 & 3 & \geq 3 \end{aligned}

$\begin{align*} 8\amp\geq3\amp3\amp\geq-8\amp3\amp\geq3 \end{align*}$

permalinkbut one of these three statements is false:

\begin{aligned} 8 & > 3 & 3 & > - 8 & 3 & \overset{no}{>} 3 \end{aligned}

$\begin{align*} 8\amp\gt3\amp3\amp\gt-8\amp3\amp\stackrel{\text{no}}{\gt}3 \end{align*}$

Remark 1.3.7.

While it may not seem helpful to write $3\geq3$ when you could write $3=3\text{,}$ the $\geq$ symbol is quite useful when specific numbers aren't used on at least one side, like in these examples:

\begin{aligned} (hourly pay rate) & \geq (minimum wage) & (age of a voter) & \geq 18 \end{aligned}

$\begin{align*} (\text{hourly pay rate})\amp\geq(\text{minimum wage})\amp(\text{age of a voter})\amp\geq18 \end{align*}$

Sometimes you want to emphasize that one number is less than another number instead of emphasizing which number is greater. To do this, we have symbols that are reversed from $\gt$ and $\geq\text{.}$ The symbol “ $\lt$ ” is the less-than symbol and it's used like this:

3 < 8

$\begin{equation*} 3\lt8 \end{equation*}$

and read out loud as “ $3$ is less than $8\text{.}$ ” To help remember which symbol is the “less than” sign and which is the “greater than” sign, notice that you can make a Less than sign with your Left hand.

Table 1.3.8 gives the complete list of all six comparison symbols. Note that we've only discussed three in this section so far, but you already know the equals symbol and have likely also seen the symbol “ $\neq\text{,}$ ” which means “not equal to.”

Symbol	Means	True	True	False
$=$	equals	$13=13$	$\frac{5}{4}=1.25$	$5\stackrel{\text{no}}{=}6$
$\gt$	is greater than	$13\gt11$	$\pi\gt3$	$9\stackrel{\text{no}}{\gt}9$
$\geq$	is greater than or equal to	$13\geq11$	$3\geq3$	$10.2\stackrel{\text{no}}{\geq}11.2$
$\lt$	is less than	$-3\lt8$	$\frac{1}{2}\lt\frac{2}{3}$	$2\stackrel{\text{no}}{\lt}-2$
$\leq$	is less than or equal to	$-3\leq8$	$3\leq3$	$\frac{4}{5}\stackrel{\text{no}}{\leq}\frac{3}{5}$
$\neq$	is not equal to	$10\neq20$	$\frac{1}{2}\neq1.2$	$\frac{3}{8}\stackrel{\text{no}}{\neq}0.375$

Table 1.3.8. Comparison Symbols

Subsection 1.3.2 Set-Builder and Interval Notation

permalinkIf you say

(age of a voter) \geq 18

$\begin{equation*} (\text{age of a voter})\geq18 \end{equation*}$

and have a particular voter in mind, what is that person's age? Maybe they are $18\text{,}$ but maybe they are older. It's helpful to use a variable $a$ to represent age (in years) and then to visualize the possibilities with a number line, as in Figure 1.3.9.

eps pdf png svg tex

Figure 1.3.9.

(age of a voter) \geq 18

$(\text{age of a voter})\geq18$

permalinkThe shaded portion of the number line in Figure 1.3.9 is a mathematical interval. For now, that just means a collection of certain numbers. In this case, it's all the numbers $18$ and above.

permalinkThe number line in Figure 1.3.9 is a graphical representation of a collection of certain numbers. We have two notations, set-builder notation and interval notation, that we also use to represent such collections of numbers.

Definition 1.3.10. Set-Builder Notation.

Set-builder notation attempts to directly tell you the condition that numbers in the interval satisfy. In general, we write set-builder notation like:

{x ∣ condition on x}

$\begin{equation*} \left\{x\mid\text{condition on }x\right\} \end{equation*}$

and read it out loud as “the set of all $x$ such that ….” For example,

{x ∣ x \geq 18}

$\begin{equation*} \left\{x\mid x\geq18\right\} \end{equation*}$

is read out loud as “the set of all $x$ such that $x$ is greater than or equal to $18\text{.}$ ” The breakdown is as follows.

$\highlight{\{}\lowlight{x\mid x\geq18}\highlight{\}}$	the set of
$\lowlight{\{}\highlight{x}\lowlight{{}\mid x\geq18\}}$	all $x$
$\lowlight{\{x}\highlight{{}\mid{}}\lowlight{x\geq18\}}$	such that
$\lowlight{\{x\mid{}}\highlight{x\geq18}\lowlight{\}}$	$x$ is greater than or equal to $18$

Definition 1.3.11. Interval Notation.

Interval notation describes a collection of numbers by telling you where the collection “starts” and “stops”. For example, in Figure 1.3.9, the interval starts at $18\text{.}$ To the right, the interval extends forever and has no end, so we use the $\infty$ symbol (meaning "infinity"). This particular interval is denoted:

[18, \infty)

$\begin{equation*} [18,\infty) \end{equation*}$

Why use “ $[$ ” on one side and “ $)$ ” on the other? The square bracket tells us that $18$ is part of the interval and the round parenthesis tells us that $\infty$ is not part of the interval. (And how could it be, since $\infty$ is not even a number?)

There are four types of infinite intervals. Take note of the different uses of round parentheses and square brackets.

eps pdf png svg tex

Figure 1.3.12. An open, infinite interval denoted by

(a, \infty)

$(a,\infty)$ means all numbers

a

$a$ or larger, not including

a .

$a\text{.}$

eps pdf png svg tex

Figure 1.3.13. A closed, infinite interval denoted by

[a, \infty)

$[a,\infty)$ means all numbers

a

$a$ or larger, including

a .

$a\text{.}$

eps pdf png svg tex

Figure 1.3.14. An open, infinite interval denoted by

(- \infty, a)

$(-\infty,a)$ means all numbers

a

$a$ or smaller, not including

a .

$a\text{.}$

eps pdf png svg tex

Figure 1.3.15. A closed, infinite interval denoted by

(- \infty, a]

$(-\infty,a]$ means all numbers

a

$a$ or smaller, including

a .

$a\text{.}$

Checkpoint 1.3.16. Interval and Set-Builder Notation from Number Lines.

Remark 1.3.17. Alternative Convention for Sketching Intervals.

When graphing an interval, an alternative convention is to use open circles and filled-in circles. An open circle can be used in place of a round parenthesis, and a filled-in circle can be used in place of a square bracket, as in this example which corresponds to the interval $(a,b]\text{.}$

a number line with marks at a and b; the portion of the number line between a and b has a thick line overlaying it; there is a hollow dot at a and solid dot at b

eps pdf png svg tex

Reading Questions 1.3.3 Reading Questions

1.

How many inequality symbols are there?

2.

What is the difference between the interval $[3,\infty)$ and the interval $(3,\infty)\text{?}$ More generally, what do square brackets and round parentheses mean in the context of interval notation?

3.

The set of numbers $\{x\mid x\leq10\}$ is being expressed using notation.

Exercises 1.3.4 Exercises

Review and Warmup

1.

Write the decimal number as a fraction.

$0.65$ =

2.

Write the decimal number as a fraction.

$0.75$ =

3.

Write the decimal number as a fraction.

$8.85$ =

4.

Write the decimal number as a fraction.

$9.45$ =

5.

Write the decimal number as a fraction.

$0.108$ =

6.

Write the decimal number as a fraction.

$0.274$ =

7.

Write the fraction as a decimal number.

${{\frac{4}{5}}}$ =
${{\frac{7}{8}}}$ =

8.

Write the fraction as a decimal number.

${{\frac{5}{8}}}$ =
${{\frac{1}{4}}}$ =

9.

Write the mixed number as a decimal number.

${3 {\textstyle\frac{5}{16}}}$ =
${1 {\textstyle\frac{11}{20}}}$ =

10.

Write the mixed number as a decimal number.

${3 {\textstyle\frac{1}{16}}}$ =
${1 {\textstyle\frac{1}{8}}}$ =

Ordering Numbers

11.

Use the $\gt$ symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4 > 3 > 2 > 1 > 0.

5 - 10 - 1 7 - 5

$\begin{equation*} {5}\quad{-10}\quad{-1}\quad{7}\quad{-5} \end{equation*}$

12.

Use the $\gt$ symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4 > 3 > 2 > 1 > 0.

7 3 8 - 1 - 6

$\begin{equation*} {7}\quad{3}\quad{8}\quad{-1}\quad{-6} \end{equation*}$

13.

Use the $\gt$ symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4 > 3 > 2 > 1 > 0.

9.02 - 3.9 - 4.17 - 4.71 - 4.81

$\begin{equation*} {9.02}\quad{-3.9}\quad{-4.17}\quad{-4.71}\quad{-4.81} \end{equation*}$

14.

Use the $\gt$ symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4 > 3 > 2 > 1 > 0.

- 8.8 8.8 3.47 7.64 - 8.7

$\begin{equation*} {-8.8}\quad{8.8}\quad{3.47}\quad{7.64}\quad{-8.7} \end{equation*}$

15.

Use the $\gt$ symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4 > 3 > 2 > 1 > 0.

- 7 3 - \frac{39}{5} 5 - \frac{33}{7}

$\begin{equation*} {-7}\quad{3}\quad{-{\frac{39}{5}}}\quad{5}\quad{-{\frac{33}{7}}} \end{equation*}$

16.

Use the $\gt$ symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4 > 3 > 2 > 1 > 0.

- \frac{31}{4} \frac{1}{2} \frac{26}{3} - 9 - 7

$\begin{equation*} {-{\frac{31}{4}}}\quad{{\frac{1}{2}}}\quad{{\frac{26}{3}}}\quad{-9}\quad{-7} \end{equation*}$

17.

Use the $\gt$ symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4 > 3 > 2 > 1 > 0.

\frac{1}{3} 9 π - 2 \frac{2}{3} \frac{π}{2}

$\begin{equation*} {{\frac{1}{3}}}\quad{9}\quad{\pi }\quad{-2}\quad{{\frac{2}{3}}}\quad{\frac{\pi }{2}} \end{equation*}$

18.

Use the $\gt$ symbol to arrange the following numbers in order from greatest to least. For example, your answer might look like 4 > 3 > 2 > 1 > 0.

2 \frac{1}{3} \frac{π}{2} 0 \sqrt{2} \frac{1}{2}

$\begin{equation*} {2}\quad{{\frac{1}{3}}}\quad{\frac{\pi }{2}}\quad{0}\quad{\sqrt{2}}\quad{{\frac{1}{2}}} \end{equation*}$

True/False

19.

Decide if each comparison is true or false.

$-8=-9$
- True
- False
$-1\neq-1$
- True
- False
$-6\gt-6$
- True
- False
$-10\neq9$
- True
- False
$7\geq-5$
- True
- False
$2=2$
- True
- False

20.

Decide if each comparison is true or false.

$-8\leq-8$
- True
- False
$-7\geq-7$
- True
- False
$-7\leq5$
- True
- False
$0\lt-4$
- True
- False
$7\gt7$
- True
- False
$-10\neq-10$
- True
- False

21.

Decide if each comparison is true or false.

$-{\frac{1}{9}}\gt-{\frac{2}{18}}$
- True
- False
$-{\frac{20}{6}}={\frac{20}{6}}$
- True
- False
${\frac{0}{7}}\neq{\frac{0}{7}}$
- True
- False
${\frac{6}{9}}={\frac{6}{9}}$
- True
- False
$-{\frac{10}{5}}\lt-{\frac{20}{10}}$
- True
- False
$-{\frac{5}{2}}\gt{\frac{43}{8}}$
- True
- False

22.

Decide if each comparison is true or false.

$-{\frac{10}{3}}\geq-{\frac{30}{9}}$
- True
- False
${\frac{31}{4}}={\frac{11}{6}}$
- True
- False
${\frac{5}{3}}\lt{\frac{19}{8}}$
- True
- False
${\frac{8}{4}}={\frac{16}{8}}$
- True
- False
$-{\frac{62}{7}}\leq{\frac{47}{8}}$
- True
- False
${\frac{43}{5}}\neq-{\frac{3}{2}}$
- True
- False

Comparisons

23.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

$\displaystyle{-\frac{9}{8}}$

<
>
=

- \frac{5}{3}

$\displaystyle{-\frac{5}{3}}$

24.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

$\displaystyle{-\frac{8}{5}}$

<
>
=

- \frac{2}{3}

$\displaystyle{-\frac{2}{3}}$

25.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

${{\frac{2}{3}}} + {{\frac{5}{2}}}$

<
>
=

\frac{3}{4} \div \frac{3}{5}

${{\frac{3}{4}}} \div {{\frac{3}{5}}}$

26.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

${{\frac{2}{5}}} + {{\frac{4}{3}}}$

<
>
=

\frac{1}{5} \div \frac{4}{5}

${{\frac{1}{5}}} \div {{\frac{4}{5}}}$

27.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

${{\frac{10}{9}}} \div {{\frac{10}{9}}}$

<
>
=

\frac{4}{10} - \frac{2}{5}

$\frac{4}{10} - \frac{2}{5}$

28.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

${{\frac{12}{11}}} \div {{\frac{12}{11}}}$

<
>
=

\frac{5}{10} - \frac{1}{2}

$\frac{5}{10} - \frac{1}{2}$

29.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

$\displaystyle{{-5 {\textstyle\frac{2}{3}}}}$

<
>
=

- 5

$\displaystyle{-5}$

30.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

$\displaystyle{{-9 {\textstyle\frac{1}{2}}}}$

<
>
=

- 9

$\displaystyle{-9}$

31.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

$\displaystyle{{-9 {\textstyle\frac{1}{2}}}}$

<
>
=

3

$\displaystyle{3}$

32.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

$\displaystyle{{-2 {\textstyle\frac{1}{3}}}}$

<
>
=

1

$\displaystyle{1}$

33.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

$\displaystyle{ \left\lvert {-{\frac{3}{4}}} \right\rvert }$

<
>
=

| 0.75 |

$\displaystyle{ \left\lvert {0.75} \right\rvert }$

34.

Choose $\lt \text{,}$ $>\text{,}$ or $=$ to make a true statement.

$\displaystyle{ \left\lvert {-{\frac{2}{5}}} \right\rvert }$

<
>
=

| 0.4 |

$\displaystyle{ \left\lvert {0.4} \right\rvert }$

Set-builder and Interval Notation

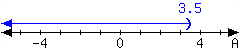
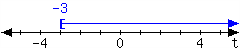
35.

For each interval expressed in the number lines, give the interval notation and set-builder notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:
eps pdf png svg tex

In set-builder notation:

In interval notation:
eps pdf png svg tex

In set-builder notation:

In interval notation:

36.

For each interval expressed in the number lines, give the interval notation and set-builder notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:
eps pdf png svg tex

In set-builder notation:

In interval notation:
eps pdf png svg tex

In set-builder notation:

In interval notation:

37.

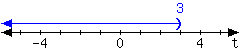
For the interval expressed in the number line, write it using set-builder notation and interval notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:

38.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:

39.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:

40.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:

41.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:

42.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:

43.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:

44.

For the interval expressed in the number line, write it using set-builder notation and interval notation.

eps pdf png svg tex

In set-builder notation:

In interval notation:

Convert to Interval Notation

45.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {{x}} \leq -7 \} }$

46.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {{x}} \leq 2 \} }$

47.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {{x}} \geq 5 \} }$

48.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {{x}} \geq 7 \} }$

49.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid{{x}} \lt 9 \} }$

50.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid{{x}} \lt -9 \} }$

51.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {{x}} \gt -7 \} }$

52.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {{x}} \gt -5 \} }$

53.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {-3} \gt {x} \} }$

54.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {-9} \gt {x} \} }$

55.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {2} \geq {x} \} }$

56.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {4} \geq {x} \} }$

57.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x\mid{7} \leq {x} \} }$

58.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x\mid{9} \leq {x} \} }$

59.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {-10} \lt {x} \} }$

60.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {-7} \lt {x} \} }$

61.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \left\{ x \mid {{{\frac{3}{7}}}} \lt {x} \right\} }$

62.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \left\{ x \mid {{{\frac{4}{7}}}} \lt {x} \right\} }$

63.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \left\{ x \mid {{x}} \leq {-{\frac{5}{3}}} \right\} }$

64.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \left\{ x \mid {{x}} \leq {-{\frac{6}{7}}} \right\} }$

65.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid {x} \leq 0 \} }$

66.

A set is written using set-builder notation. Write it using interval notation.

$\displaystyle{ \{ x \mid 0 \lt {x} \} }$