Section 7.5 Solving Quadratic Equations Chapter Review
¶Subsection 7.5.1 Solving Quadratic Equations by Using a Square Root
In Section 7.1 we covered how to solve quadratic equations using the square root property and how to use the Pythagorean Theorem.
Example 7.5.1. Solving Quadratic Equations Using the Square Root Property.
Solve for \(w\) in \(3(2-w)^2-24=0\text{.}\)
It's important here to suppress any urge you may have to expand the squared binomial. We begin by isolating the squared expression.
Now that we have the squared expression isolated, we can use the square root property.
The solution set is \(\left\{2\sqrt{2}+2,-2\sqrt{2}+2\right\}\text{.}\)
Example 7.5.2. The Pythagorean Theorem.
Faven was doing some wood working in her garage. She needed to cut a triangular piece of wood for her project that had a hypotenuse of \(16\) inches, and the sides of the triangle should be equal in length. How long should she make her sides?
Let's start by representing the length of the triangle, measured in inches, by the letter \(x\text{.}\) That would also make the other side \(x\) inches long.
Faven should now set up the Pythagorean theorem regarding the picture. That would be
Solving this equation, we have:
Faven should make the sides of her triangle about \(11.3\) inches long to force the hypotenuse to be \(16\) inches long.
Subsection 7.5.2 The Quadratic Formula
In Section 7.2 we covered how to use the quadratic formula to solve any quadratic equation.
Example 7.5.4. Solving Quadratic Equations with the Quadratic Formula.
Solve the equations using the quadratic formula.
\(x^2+4x=6\)
\(5x^2-2x+1=0\)
-
First we should change the equation into standard form.
\begin{align*} x^2+4x\amp=6\\ x^2+4x-6\amp=0 \end{align*}Next, we check and see that we cannot factor the left side or use the square root property so we must use the quadratic formula. We identify that \(\substitute{a=1}\text{,}\) \(\substitute{b=4}\text{,}\) and \(\substitute{c=-6}\text{.}\) We will substitute them into the quadratic formula:
\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-\substitute{4}\pm\sqrt{(\substitute{4})^2-4(\substitute{1})(\substitute{-6})}}{2(\substitute{1})}\\ \amp=\frac{-4\pm\sqrt{16+24}}{2}\\ \amp=\frac{-4\pm\sqrt{40}}{2}\\ \amp=\frac{-4\pm\sqrt{\highlight{4}\cdot10}}{2}\\ \amp=\frac{-4\pm\sqrt{\highlight{4}}\cdot\sqrt{10}}{2}\\ \amp=\frac{-4\pm\highlight{2}\sqrt{10}}{2}\\ \amp=-\frac{4}{2}\pm\frac{2\sqrt{10}}{2}\\ \amp=-2\pm\sqrt{10} \end{align*}So the solution set is \(\left\{-2+\sqrt{10},-2-\sqrt{10}\right\}\text{.}\)
-
Since the equation \(5x^2-2x+1=0\) is already in standard form, we check and see that we cannot factor the left side or use the square root property so we must use the quadratic formula. We identify that \(\substitute{a=5}\text{,}\) \(\substitute{b=-2}\text{,}\) and \(\substitute{c=1}\text{.}\) We will substitute them into the quadratic formula:
\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-\substitute{(-2)}\pm\sqrt{\substitute{(-2)}^2-4(\substitute{5})(\substitute{1})}}{2(\substitute{5})}\\ \amp=\frac{2\pm\sqrt{4-20}}{10}\\ \amp=\frac{2\pm\sqrt{-16}}{10} \end{align*}Since the solutions have square roots of negative numbers, we must conclude that there are no real solutions.
Subsection 7.5.3 Complex Solutions to Quadratic Equations
In Section 7.3 we covered what both imaginary numbers and complex numbers are, as well as how to solve quadratic equations where the solutions are imaginary numbers or complex numbers.
Example 7.5.5. Imaginary Numbers.
Simplify the expression \(\sqrt{-12}\) using the imaginary number, \(i\text{.}\)
Start by splitting the \(-1\) from the \(12\) and by looking for the largest perfect-square factor of \(-12\text{,}\) which happens to be \(4\text{.}\)
Example 7.5.6. Solving Quadratic Equations with Imaginary Solutions.
Solve for \(m\) in \(2m^2+16=0\text{,}\) where \(p\) is an imaginary number.
There is no \(m\) term so we will use the square root method.
The solution set is \(\left\{-\firsthighlight{2}\secondhighlight{i}\sqrt{2},\firsthighlight{2}\secondhighlight{i}\sqrt{2}\right\}\text{.}\)
Example 7.5.7. Solving Quadratic Equations with Complex Solutions.
Solve the equation \(3(v-2)^2+54=0\text{,}\) where \(v\) is a complex number.
So, the solution set is \(\left\{2+\firsthighlight{3}\secondhighlight{i}\sqrt{2},2-\firsthighlight{3}\secondhighlight{i}\sqrt{2}\right\}\text{.}\)
Subsection 7.5.4 Solving Equations in General
In Section 2.1 we learned how to solve linear equations. In Section 6.4 we learned how to solve radical equations. In Section 7.1 and Section, we learned how to solve quadratic equations.
Then in Section 7.4 we looked at a few strategies to solve equations in general, often relying on those earlier specific techniques.
Example 7.5.8. Equations where the Variable Appears Once.
Solve the equations using an effective method.
\((x-4)^2-2=0\)
\(\sqrt{3x+2}-2=5\)
\(3(5x-6)-7=2\)
-
Since the variable \(x\) only appears once, we can apply steps one at a time to undo all of the operations that are done to \(x\) and eventually isolate it.
\begin{align*} (x-4)^2-2\amp=0\\ (x-4)^2\amp=2\\ x-4\amp=\pm\sqrt{2}\\ x\amp=4\pm\sqrt{2} \end{align*}So the solution set is \(\left\{4+\sqrt{2},4-\sqrt{2}\right\}\)
-
Since the variable \(x\) only appears once, we can apply steps one at a time to undo all of the operations that are done to \(x\) and eventually isolate it.
\begin{align*} \sqrt{3x+2}-2\amp=5\\ \sqrt{3x+2}\amp=7\\ \left(\sqrt{3x+2}\right)^2\amp=7^2\\ 3x+2\amp=49\\ 3x\amp=47\\ x\amp=\frac{47}{3} \end{align*}At this point \(\frac{47}{3}\) is only a potential solution. We may have introduced an extraneous solution at the point where we squared both sides. So we should check it.
\begin{align*} \sqrt{3\cdot\substitute{\frac{47}{3}}+2}-2\amp\stackrel{?}{=}5\\ \sqrt{47+2}\amp\stackrel{?}{=}7\\ \sqrt{49}\amp\stackrel{\checkmark}{=}7 \end{align*}So, the solution set is \(\left\{\frac{47}{3}\right\}\text{.}\)
-
Since the variable \(x\) only appears once, we can apply steps one at a time to undo all of the operations that are done to \(x\) and eventually isolate it.
\begin{align*} 3(5x-6)-7\amp=2\\ 3(5x-6)\amp=9\\ 5x-6\amp=3\\ 5x\amp=9\\ x\amp=\frac{9}{5} \end{align*}The solution set is \(\left\{\frac{9}{5}\right\}\text{.}\)
Example 7.5.9. Equations With More Than One Instance of the Variable.
Recognize that these equations have more than one instance of the variable, so it is not immediately possible to isolate the variable by undoing the operations that are done to it. Instead, call upon a special technique to solve the equation.
\((x-4)^2+2x=0\)
\(16x-2(3x-1)=7\)
\(\sqrt{x+2}=x-4\)
-
To solve the equation \((x-4)^2+2x=0\text{,}\) note that it is a quadratic equation, and we can write it in standard form.
\begin{align*} (x-4)^2+2x\amp=0\\ x^2-8x+16+2x\amp=0\\ x^2-6x+16\amp=0 \end{align*}Now we may use the quadratic formula 7.2.2.
\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-(-6)\pm\sqrt{(-6)^2-4(1)(16)}}{2(1)}\\ \amp=\frac{6\pm\sqrt{36-48}}{2}\\ \amp=\frac{6\pm\sqrt{-12}}{2}\\ \end{align*}At this point, we notice that the solutions are complex. Continue to simplify until they are completely reduced.
\begin{align*} x\amp=\frac{6\pm\sqrt{\firsthighlight{4}\cdot\secondhighlight{-1}\cdot3}}{2}\\ \amp=\frac{6\pm\sqrt{\firsthighlight{4}}\cdot\sqrt{\secondhighlight{-1}}\cdot\sqrt{3}}{2}\\ \amp=\frac{6\pm\firsthighlight{2}\secondhighlight{i}\sqrt{3}}{2}\\ \amp=\frac{6}{2}\pm\frac{2i\sqrt{3}}{2}\\ \amp=3\pm i\sqrt{3} \end{align*}So the solution set is \(\left\{3-i\sqrt{3},3+i\sqrt{3}\right\}\text{.}\)
-
To solve the equation \(16x-2(3x-1)=3\) we first we first note that it is linear. Since it is linear, we just need to follow the steps outlined in Process 2.1.4.
\begin{align*} 16x-2(3x-1)\amp=7\\ 16x-6x+3\amp=7\\ 10x+3\amp=7\\ 10x\amp=4\\ x\amp=\frac{4}{10}\\ x\amp=\frac{2}{5} \end{align*}So, the solution set is \(\left\{\frac{2}{5}\right\}\text{.}\)
-
Since the equation \(\sqrt{x+2}=x-4\) is a radical equation, we should isolate the radical (which it already is) and square both sides of the equation.
\begin{align*} \sqrt{x+2}\amp=x-4\\ \left(\sqrt{x+2}\right)^2\amp=\left(x-4\right)^2\\ x+2\amp=x^2-8x+16\\ 0\amp=x^2-9x+14 \end{align*}Since the equation is now quadratic, we may use the quadratic formula 7.2.2 to solve it.
\begin{align*} x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ x\amp=\frac{-(-9)\pm\sqrt{(-9)^2-4(1)(14)}}{2(1)}\\ \amp=\frac{9\pm\sqrt{81-56}}{2}\\ \amp=\frac{9\pm\sqrt{25}}{2}\\ \amp=\frac{9\pm5}{2} \end{align*}\begin{align*} x\amp=\frac{9-5}{2}\amp\amp\text{or}\amp x\amp=\frac{9+5}{2}\\ x\amp=\frac{4}{2}\amp\amp\text{or}\amp x\amp=\frac{14}{2}\\ x\amp=2\amp\amp\text{or}\amp x\amp=7 \end{align*}Since this is a radical equation, we should verify our solutions and look out for “extraneous solutions”.
\begin{align*} \sqrt{\substitute{2}+2}\amp\stackrel{?}{=}\substitute{2}-4\amp\amp\text{or}\amp\sqrt{\substitute{7}+2}\amp\stackrel{?}{=}\substitute{7}-4\\ \sqrt{4}\amp\stackrel{\text{no}}{=}-2\amp\amp\text{or}\amp\sqrt{9}\amp\stackrel{\text{\checkmark}}{=}3 \end{align*}So the solution set is \(\{7\}\text{.}\)
Example 7.5.10. Solving For a Variable in Terms of Other Variables.
Often in science classes, you are given a formula that needs to be rearranged to be useful to a situation. Below are a few equations from physics that describe the natural world.
Solve the equation \(v^2=v_0^2+2ax\) for \(x\text{.}\) (This equation describes the motion of objects that are accelerating.)
Solve the equation \(c \ell=\ell_0\sqrt{c^2-v^2}\) for \(v\text{.}\) (This equation describes the size of things moving at very fast speeds.)
Solve the equation \(y=\frac{\alpha t^2}{2}+vt\) for \(t\text{.}\) (This is another equation that describes the motion of objects that are accelerating.)
-
Since \(x\) only appears once in the euqation, we only need to undo the operations that are done to it.
\begin{align*} v^2\amp=v_0^2+2ax\\ v^2-v_0^2\amp=2ax\\ \frac{v^2-v_0^2}{2a}\amp=x \end{align*}So we find \(x=\frac{v^2-v_0^2}{2a}\text{.}\)
-
Since \(v\) only appears once in the euqation, we only need to undo the operations that are done to it. According to the order of operations, on the right side of the equation,
\(v\) is squared.
The result is negated.
The result is added to \(c^2\text{.}\)
The result has a square root applied.
The result is multiplied by \(\ell_0\text{.}\)
So we do all of the opposite things in the opposite order.
\begin{align*} c \ell\amp=\ell_0\sqrt{c^2-v^2}\\ \frac{c\cdot \ell}{\ell_0}\amp=\sqrt{c^2-v^2}\\ \left(\frac{c\cdot \ell}{\ell_0}\right)^2\amp=\left(\sqrt{c^2-v^2}\right)^2\\ \left(\frac{c\cdot \ell}{\ell_0}\right)^2\amp=c^2-v^2\\ \left(\frac{c\cdot \ell}{\ell_0}\right)^2-c^2\amp=-v^2\\ -\left(\frac{c\cdot \ell}{\ell_0}\right)^2+c^2\amp=v^2\\ \pm\sqrt{-\left(\frac{c\cdot \ell}{\ell_0}\right)^2+c^2}\amp=v\\ \pm\sqrt{c^2-\left(\frac{c\cdot \ell}{\ell_0}\right)^2}\amp=v \end{align*}So, we find \(v=\pm\sqrt{c^2-\left(\frac{c\cdot \ell}{\ell_0}\right)^2}\text{.}\)
-
This is a quadratic equtaion when we view \(t\) as the variable. First, we should rearrange the equation to standard form.
\begin{align*} y\amp=\frac{\alpha t^2}{2}+vt\\ 0\amp=\frac{\alpha }{2}t^2+vt-y \end{align*}It is helpful with many equations to “clear denominators”. In this case, that means multiplying each side of the equation by \(2\text{.}\)
\begin{align*} 0\amp=\alpha t^2+2vt-2y \end{align*}Now, we may apply the quadratic formula 7.2.2.
\begin{align*} t\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ t\amp=\frac{-2v\pm\sqrt{(2v)^2-4\alpha (-2y)}}{2\alpha}\\ t\amp=\frac{-2v\pm\sqrt{4v^2+8\alpha y}}{2\alpha}\\ t\amp=\frac{-2v\pm\sqrt{4\left(v^2+2\alpha y\right)}}{2\alpha}\\ t\amp=\frac{-2v\pm2\sqrt{v^2+2\alpha y}}{2\alpha}\\ t\amp=\frac{-v\pm \sqrt{v^2+2\alpha y}}{\alpha} \end{align*}So we find \(t=\frac{-v\pm\sqrt{v^2+2\alpha y}}{\alpha}\text{.}\)
Exercises 7.5.5 Exercises
Solving Quadratic Equations by Using a Square Root
1.
Solve the equation.
\(x^2 = 27\)
2.
Solve the equation.
\(x^2 = 63\)
3.
Solve the equation.
\(64x^2 = 9\)
4.
Solve the equation.
\(4x^2 = 81\)
5.
Solve the equation.
\(\left(x+6\right)^2 = 36\)
6.
Solve the equation.
\(\left(x+9\right)^2 = 4\)
7.
Solve the equation.
\(-4 - 5 ( x - 9 )^2 = -9\)
8.
Solve the equation.
\(18 - 3 ( x - 9 )^2 = 6\)
9.
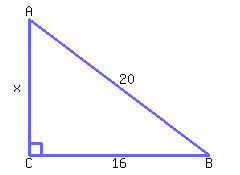
Find the value of \(x\text{.}\)
\(x={}\)
10.
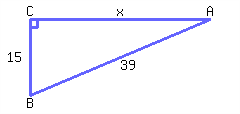
Find the value of \(x\text{.}\)
\(x={}\)
11.
Devon is designing a rectangular garden. The garden’s diagonal must be \(64.6\) feet, and the ratio between the garden’s base and height must be \(15:8\text{.}\) Find the length of the garden’s base and height.
The garden’s base is feet and its height is .
12.
Tammy is designing a rectangular garden. The garden’s diagonal must be \(13.5\) feet, and the ratio between the garden’s base and height must be \(4:3\text{.}\) Find the length of the garden’s base and height.
The garden’s base is feet and its height is .
The Quadratic Formula
13.
Solve the equation.
\({28x^{2}+29x+6}=0\)
14.
Solve the equation.
\({24x^{2}+29x-4}=0\)
15.
Solve the equation.
\({x^{2}}= {-7x-11}\)
16.
Solve the equation.
\({x^{2}}= {7x-11}\)
17.
Solve the equation.
\({4x^{2}+4x+6}= 0\)
18.
Solve the equation.
\({2x^{2}+7x+7}= 0\)
19.
Solve the equation.
\(x^2 - 26x= 0\)
20.
Solve the equation.
\(x^2 - 6x= 0\)
21.
Solve the equation.
\({x^{2}-7x} = {18}\)
22.
Solve the equation.
\({x^{2}-x} = {20}\)
23.
Solve the equation.
\({x^{2}}= {9x-19}\)
24.
Solve the equation.
\({x^{2}}= {-5x-5}\)
25.
An object is launched upward at the height of \(200\) meters. Its height can be modeled by
where \(h\) stands for the object’s height in meters, and \(t\) stands for time passed in seconds since its launch. The object’s height will be \(240\) meters twice before it hits the ground. Find how many seconds since the launch would the object’s height be \(240\) meters. Round your answers to two decimal places if needed.
The object’s height would be \(240\) meters the first time at seconds, and then the second time at seconds.
26.
An object is launched upward at the height of \(220\) meters. Its height can be modeled by
where \(h\) stands for the object’s height in meters, and \(t\) stands for time passed in seconds since its launch. The object’s height will be \(230\) meters twice before it hits the ground. Find how many seconds since the launch would the object’s height be \(230\) meters. Round your answers to two decimal places if needed.
The object’s height would be \(230\) meters the first time at seconds, and then the second time at seconds.
Complex Solutions to Quadratic Equations
27.
Simplify the radical and write it as a complex number using \(i\text{.}\)
\(\displaystyle{ \sqrt{-40} =}\)
28.
Simplify the radical and write it as a complex number using \(i\text{.}\)
\(\displaystyle{ \sqrt{-56} =}\)
29.
Solve the quadratic equation. Solutions could be complex numbers.
\({-2y^{2}} - 5 = 1\)
30.
Solve the quadratic equation. Solutions could be complex numbers.
\({3r^{2}} + 8 = 2\)
31.
Solve the quadratic equation. Solutions could be complex numbers.
\(-5(r+4)^2+5 = 85\)
32.
Solve the quadratic equation. Solutions could be complex numbers.
\(3(t - 6)^2+5 = -295\)
Solving Equations in General
33.
Solve the equation.
\(\displaystyle{ {\sqrt{t}+72} = {t} }\)
34.
Solve the equation.
\(\displaystyle{ {\sqrt{x}+30} = {x} }\)
35.
Solve the equation.
\(\displaystyle{ {5+10\!\left(y-5\right)}={-6-\left(7-2y\right)} }\)
36.
Solve the equation.
\(\displaystyle{ {3+8\!\left(t-3\right)}={1-\left(2-3t\right)} }\)
37.
Solve the equation.
\({x^{2}+5x} = {24}\)
38.
Solve the equation.
\({x^{2}+8x} = {9}\)
39.
Solve the equation.
\(\displaystyle{ -8-8A+2 = -A+12-7A }\)
40.
Solve the equation.
\(\displaystyle{ -6-10C+6 = -C+13-9C }\)
41.
Solve the equation.
\({x^{2}+8x+3}= 0\)
42.
Solve the equation.
\({x^{2}-6x-9}= 0\)
43.
Solve the equation.
\(-7 - 2 ( x+2 )^2 = -9\)
44.
Solve the equation.
\(30 - 6 ( x+2 )^2 = 6\)
45.
Solve the equation.
\(\displaystyle{ {14}={\frac{t}{5}+\frac{t}{2}} }\)
46.
Solve the equation.
\(\displaystyle{ {3}={\frac{a}{3}+\frac{a}{6}} }\)
47.
Solve the equation.
\(\displaystyle{ {y} = {\sqrt{y+4}+86} }\)
48.
Solve the equation.
\(\displaystyle{ {r} = {\sqrt{r+2}+40} }\)
49.
Solve the equation.
\(3x^2 + 41= 0\)
50.
Solve the equation.
\(43x^2 + 47= 0\)
51.
Solve the equation.
\({5x^{2}}={-42x-49}\)
52.
Solve the equation.
\({2x^{2}}={-21x-10}\)
53.
Solve the equation.
\(\displaystyle{ {x} = {\sqrt{x-1}+7} }\)
54.
Solve the equation.
\(\displaystyle{ {x} = {\sqrt{x+7}-1} }\)