ORCCA Percentages

Section 2.7 Percentages

Objectives PCC Course Content and Outcome Guide

Percent-related problems arise in everyday life. This section reviews some basic calculations that can be made with percentages.

Figure 2.7.1 Alternative Video Lesson

In many situations when translating from English to math, the word “of” translates as multiplication. Also the word “is” (and many similar words related to “to be”) translates to an equals sign. For example:

\begin{aligned} One third & of thirty is ten. \\ \frac{1}{3} & \cdot 30 = 10 \end{aligned}

$\begin{align*} \text{One third }\amp\text{of thirty is ten.}\\ \frac{1}{3}\amp\cdot30=10 \end{align*}$

Here is another example, this time involving a percentage. We know that “ $2$ is $50\%$ of $4\text{,}$ ” so we can say:

\begin{aligned} 2 & is 50 % of 4 \\ 2 & = 0.5 \cdot 4 \end{aligned}

$\begin{align*} 2\amp\text{ is } 50\% \text{ of } 4\\ 2\amp= 0.5\cdot4 \end{align*}$

Example 2.7.2

Translate each statement involving percents below into an equation. Define any variables used. (Solving these equations is an exercise).

How much is $30\%$ of $\$24.00\text{?}$
$\$7.20$ is what percent of $\$24.00\text{?}$
$\$7.20$ is $30\%$ of how much money?

Explanation

Each question can be translated from English into a math equation by reading it slowly and looking for the right signals.

The word “is” means about the same thing as the equals sign. “How much” is a question phrase, and we can let $x$ be the unknown amount (in dollars). The word “of” translates to multiplication, as discussed earlier. So we have:

\begin{equation*} \pinover{x}{how\ much}\pinover{=}{is}\pinover{0.30}{30\%}\pinover{\cdot}{of}\pinover{24}{\$24} \end{equation*}
Let $P$ be the unknown value. We have:

\begin{equation*} \pinover{7.2}{\$7.20}\pinover{=}{is}\pinover{P}{what\ percent}\pinover{\cdot}{of}\pinover{24}{\$24} \end{equation*}

With this setup, $P$ is going to be a decimal value ($0.30$) that you would translate into a percentage ($30\%$).
Let $x$ be the unknown amount (in dollars). We have:

\begin{equation*} \pinover{7.2}{\$7.20}\pinover{=}{is}\pinover{0.30}{30\%}\pinover{\cdot}{of}\pinover{x}{how\ much} \end{equation*}

Checkpoint 2.7.3

Solve each equation from Example 2.7.2.

Subsection 2.7.1 Setting up and Solving Percent Equations

An important skill for solving percent-related problems is to boil down a complicated word problem into a simple form like “ $2$ is $50\%$ of $4\text{.}$ ” Let's look at some further examples.

Example 2.7.4

In Fall 2016, Portland Community College had $89{,}900$ enrolled students. According to Figure 2.7.5, how many black students were enrolled at PCC in Fall 2016?

a pie chart that indicates white students are 68%; Hispanic students are 11%; Asian students are 8%; black students are 6%; and students of other ethnicities make up 7%

eps pdf png svg tex

Figure 2.7.5 Racial breakdown of PCC students in Fall 2016

Explanation

After reading this word problem and the chart, we can translate the problem into “what is $6\%$ of $89{,}900\text{?}$” Let $x$ be the number of black students enrolled at PCC in Fall 2016. We can set up and solve the equation:

\begin{align*} \pinover{x}{what}\amp\pinover{=}{is}\pinover{0.06}{6\%}\pinover{\cdot}{of}\pinover{89900}{89,900}\\ x\amp=5394 \end{align*}

There was not much “solving” to do, since the variable we wanted to isolate was already isolated.

As of Fall 2016, Portland Community College had $5394$ black students. Note: this is not likely to be perfectly accurate, because the numbers we started with ($89{,}900$ enrolled students and $6\%$) appear to be rounded.

Example 2.7.6

The bar graph in Figure 2.7.7 displays how many students are in each class at a local high school. According to the bar graph, what percentage of the school's student population is freshman?

a bar graph indicating there are 134 freshmen, 103 sophomores, 96 juniors, and 86 seniors

eps pdf png svg tex

Figure 2.7.7 Number of students at a high school by class

Explanation

The school's total number of students is:

\begin{equation*} 134+103+96+86=419 \end{equation*}

With that calculated, we can translate the main question:

“What percentage of the school's student population is freshman?”

into:

“What percent of $419$ is $134\text{?}$”

Using $P$ to represent the unknown quantity, we write and solve the equation:

\begin{align*} \pinover{P}{what\ percent}\pinover{\cdot}{of}\pinover{419}{419}\amp\pinover{=}{is}\pinover{134}{134}\\ \divideunder{P\cdot 419}{419}\amp=\divideunder{134}{419}\\ P\amp\approx0.3198\\ P\amp\approx31.98\% \end{align*}

Approximately $31.98\%$ of the school's student population is freshman.

Remark 2.7.8

When solving equations that do not have context we state the solution set. However, when solving an equation or inequality that arises in an application problem (such as the context of the high school in Example 2.7.6), it makes more sense to summarize our result with a sentence, using the context of the application. This allows us to communicate the full result, including appropriate units.

Example 2.7.9

Carlos just received his monthly paycheck. His gross pay (the amount before taxes and related things are deducted) was $\$2{,}346.19\text{,}$ and his total tax and other deductions was $\$350.21\text{.}$ The rest was deposited directly into his checking account. What percent of his gross pay went into his checking account?

Explanation

Train yourself to read the word problem and not try to pick out numbers to substitute into formulas. You may find it helps to read the problem over to yourself three or more times before you attempt to solve it. There are three dollar amounts to discuss in this problem, and many students fall into a trap of using the wrong values in the wrong places. There is the gross pay, the amount that was deducted, and the amount that was deposited. Only two of these have been explicitly written down. We need to use subtraction to find the dollar amount that was deposited:

\begin{equation*} 2346.19-350.21=1995.98 \end{equation*}

Now, we can translate the main question:

“What percent of his gross pay went into his checking account?”

into:

“What percent of $\$2346.19$ is $\$1995.98\text{?}$”

Using $P$ to represent the unknown quantity, we write and solve the equation:

\begin{align*} \pinover{P}{what\ percent}\pinover{\cdot}{of}\pinover{2346.19}{\$2346.19}\amp\pinover{=}{is}\pinover{1995.98}{\$1995.98}\\ \divideunder{P\cdot 2346.19}{2346.19}\amp=\divideunder{1995.98}{2346.19}\\ P\amp\approx0.8507\\ P\amp\approx85.07\% \end{align*}

Approximately $85.07\%$ of his gross pay went into his checking account.

Checkpoint 2.7.10

Example 2.7.11

According to e-Literate, the average cost of a new college textbook has been increasing. Find the percentage of increase from 2009 to 2013.

a plot over time indicating average textbook price was $62.00 in 2009; $65.11 in 2010; $68.87 in 2011; $72.11 in 2012; and $79.00 in 2013

eps pdf png svg tex

Figure 2.7.12 Average New Textbook Price from 2009 to 2013

Explanation

The actual amount of increase from 2009 to 2013 was $79-62=17\text{,}$ dollars. We need to answer the question “$\$17$ is what percent of $\$62\text{?}$” Note that we are comparing the $17$ to $62\text{,}$ not to $79\text{.}$ In these situations where one amount is the earlier amount, the earlier original amount is the one that represents $100\%\text{.}$ Let $P$ represent the percent of increase. We can set up and solve the equation:

\begin{align*} \pinover{17}{\$17}\amp\pinover{=}{is}\pinover{P}{what\ percent}\pinover{\cdot}{of}\pinover{62}{\$62}\\ 17\amp=62P\\ \divideunder{17}{62}\amp=\divideunder{62P}{62}\\ 0.2742\amp\approx P \end{align*}

From 2009 to 2013, the average cost of a new textbook increased by approximately $27.42\%\text{.}$

Checkpoint 2.7.13

Example 2.7.14

Enrollment at your neighborhood's elementary school two years ago was $417$ children. After a $15\%$ increase last year and a $15\%$ decrease this year, what's the new enrollment?

Explanation

It is tempting to think that increasing by $15\%$ and then decreasing by $15\%$ would bring the enrollment right back to where it started. But the $15\%$ decrease applies to the enrollment after it had already increased. So that $15\%$ decrease is going to translate to more students lost than were gained.

Using $100\%$ as corresponding to the enrollment from two years ago, the enrollment last year was $100\%+15\%=115\%$ of that. But then using $100\%$ as corresponding to the enrollment from last year, the enrollment this year was $100\%-15\%=85\%$ of that. So we can set up and solve the equation

\begin{align*} \pinover{x}{this\ \text{year's}\ enrollment}\amp\pinover{=}{is}\pinover{0.85}{85\%}\pinover{\cdot}{of}\pinover{1.15}{115\%}\pinover{\cdot}{of}\pinover{417}{enrollment\ two\ years\ ago}\\ x\amp=0.85\cdot1.15\cdot417\\ x\amp=407.6175 \end{align*}

We would round and report that enrollment is now $408$ students. (The percentage rise and fall of $15\%$ were probably rounded in the first place, which is why we did not end up with a whole number.)

Subsection 2.7.2 Exercises

Review and Warmup

1

Change the following percentages into decimals:

$\displaystyle{ 17\% = }$

$\displaystyle{ 54\% = }$

2

Change the following percentages into decimals:

$\displaystyle{ 18\% = }$

$\displaystyle{ 51\% = }$

3

Convert the following decimals into percentages:

$\displaystyle{ 0.29 = }$

$\displaystyle{ 0.67 = }$

4

Convert the following decimals into percentages:

$\displaystyle{ 0.21 = }$

$\displaystyle{ 0.64 = }$

5

Change the following percentages into decimals:

$\displaystyle{ 3\% = }$

$\displaystyle{ 30\% = }$

$\displaystyle{ 100\% = }$

$\displaystyle{ 300\% = }$

6

Change the following percentages into decimals:

$\displaystyle{ 4\% = }$

$\displaystyle{ 40\% = }$

$\displaystyle{ 100\% = }$

$\displaystyle{ 400\% = }$

7

Convert the following decimals into percentages:

$\displaystyle{ 0.05 = }$

$\displaystyle{ 0.5 = }$

$\displaystyle{ 5 = }$

$\displaystyle{ 1 = }$

8

Convert the following decimals into percentages:

$\displaystyle{ 0.06 = }$

$\displaystyle{ 0.6 = }$

$\displaystyle{ 6 = }$

$\displaystyle{ 1 = }$

9

Convert the following decimals into percentages:

$\displaystyle{ 6.67 = }$

$\displaystyle{ 0.667 = }$

$\displaystyle{ 0.0667 = }$

10

Convert the following decimals into percentages:

$\displaystyle{ 7.22 = }$

$\displaystyle{ 0.722 = }$

$\displaystyle{ 0.0722 = }$

11

Change the following percentages into decimals:

$\displaystyle{ 895\% = }$

$\displaystyle{ 89.5\% = }$

$\displaystyle{ 8.95\% = }$

12

Change the following percentages into decimals:

$\displaystyle{ 959\% = }$

$\displaystyle{ 95.9\% = }$

$\displaystyle{ 9.59\% = }$

Basic Percentage Calculation

13

$3\%$ of $200$ is .

14

$8\%$ of $300$ is .

15

$60\%$ of $400$ is .

16

$30\%$ of $490$ is .

17

$780\%$ of $590$ is .

18

$530\%$ of $690$ is .

19

Answer with a percent.

$176$ is of $220\text{.}$

20

Answer with a percent.

$720$ is of $800\text{.}$

21

Answer with a percent.

$142.1$ is of $49\text{.}$

22

Answer with a percent.

$21.6$ is of $18\text{.}$

23

Answer with a percent.

$12$ is about of $47\text{.}$

24

Answer with a percent.

$8$ is about of $44\text{.}$

25

$14\%$ of is $68.6\text{.}$

26

$72\%$ of is $424.8\text{.}$

27

$4\%$ of is $27.6\text{.}$

28

$9\%$ of is $71.1\text{.}$

29

$420\%$ of is $3738\text{.}$

30

$250\%$ of is $2450\text{.}$

Applications

31

A town has $1400$ registered residents. Among them, $39\%$ were Democrats, $38\%$ were Republicans. The rest were Independents. How many registered Independents live in this town?

There are registered Independent residents in this town.

32

A town has $1800$ registered residents. Among them, $36\%$ were Democrats, $27\%$ were Republicans. The rest were Independents. How many registered Independents live in this town?

There are registered Independent residents in this town.

33

Martha is paying a dinner bill of ${\$29.00}\text{.}$ Martha plans to pay $12\%$ in tips. How much tip will Martha pay?

Martha will pay in tip.

34

Evan is paying a dinner bill of ${\$33.00}\text{.}$ Evan plans to pay $20\%$ in tips. How much tip will Evan pay?

Evan will pay in tip.

35

Ashley is paying a dinner bill of ${\$36.00}\text{.}$ Ashley plans to pay $16\%$ in tips. How much in total (including bill and tip) will Ashley pay?

Ashley will pay in total (including bill and tip).

36

Rita is paying a dinner bill of ${\$40.00}\text{.}$ Rita plans to pay $12\%$ in tips. How much in total (including bill and tip) will Rita pay?

Rita will pay in total (including bill and tip).

37

A watch’s wholesale price was ${\$440.00}\text{.}$ The retailer marked up the price by $40\%\text{.}$ What’s the watch’s new price (markup price)?

The watch’s markup price is .

38

A watch’s wholesale price was ${\$460.00}\text{.}$ The retailer marked up the price by $30\%\text{.}$ What’s the watch’s new price (markup price)?

The watch’s markup price is .

39

In the past few seasons’ basketball games, Timothy attempted $170$ free throws, and made $153$ of them. What percent of free throws did Timothy make?

Timothy made of free throws in the past few seasons.

40

In the past few seasons’ basketball games, Nina attempted $430$ free throws, and made $86$ of them. What percent of free throws did Nina make?

Nina made of free throws in the past few seasons.

41

A painting is on sale at ${\$360.00}\text{.}$ Its original price was ${\$450.00}\text{.}$ What percentage is this off its original price?

The painting was off its original price.

42

A painting is on sale at ${\$450.00}\text{.}$ Its original price was ${\$500.00}\text{.}$ What percentage is this off its original price?

The painting was off its original price.

43

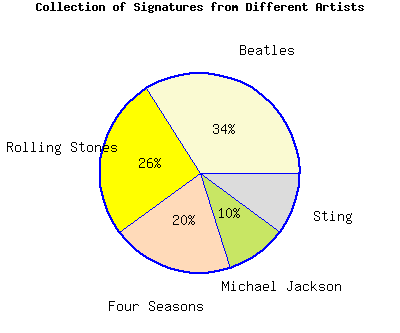
The pie chart represents a collector’s collection of signatures from various artists.

eps pdf png svg tex

If the collector has a total of $1050$ signatures, there are signatures by Sting.

44

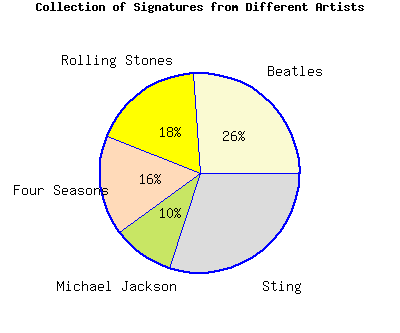
The pie chart represents a collector’s collection of signatures from various artists.

eps pdf png svg tex

If the collector has a total of $1250$ signatures, there are signatures by Sting.

45

In the last election, $34\%$ of a county’s residents, or $12240$ people, turned out to vote. How many residents live in this county?

This county has residents.

46

In the last election, $59\%$ of a county’s residents, or $23836$ people, turned out to vote. How many residents live in this county?

This county has residents.

47

$70.68$ grams of pure alcohol was used to produce a bottle of $18.6\%$ alcohol solution. What is the weight of the solution in grams?

The alcohol solution weighs .

48

$43.6$ grams of pure alcohol was used to produce a bottle of $10.9\%$ alcohol solution. What is the weight of the solution in grams?

The alcohol solution weighs .

49

Connor paid a dinner and left $17\%\text{,}$ or ${\$3.74}\text{,}$ in tips. How much was the original bill (without counting the tip)?

The original bill (not including the tip) was .

50

Sydney paid a dinner and left $13\%\text{,}$ or ${\$3.38}\text{,}$ in tips. How much was the original bill (without counting the tip)?

The original bill (not including the tip) was .

51

Rebecca sells cars for a living. Each month, she earns ${\$2{,}000.00}$ of base pay, plus a certain percentage of commission from her sales.

One month, Rebecca made ${\$52{,}500.00}$ in sales, and earned a total of ${\$3{,}186.50}$ in that month (including base pay and commission). What percent commission did Rebecca earn?

Rebecca earned in commission.

52

Ryan sells cars for a living. Each month, he earns ${\$2{,}000.00}$ of base pay, plus a certain percentage of commission from his sales.

One month, Ryan made ${\$57{,}000.00}$ in sales, and earned a total of ${\$4{,}644.80}$ in that month (including base pay and commission). What percent commission did Ryan earn?

Ryan earned in commission.

53

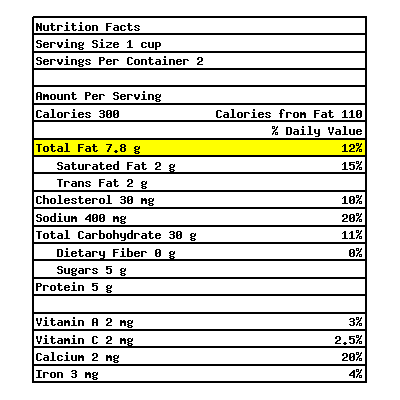
The following is a nutrition fact label from a certain macaroni and cheese box.

eps pdf png svg tex

The highlighted row means each serving of macaroni and cheese in this box contains ${7.8\ {\rm g}}$ of fat, which is $12\%$ of an average person’s daily intake of fat. What’s the recommended daily intake of fat for an average person?

The recommended daily intake of fat for an average person is .

54

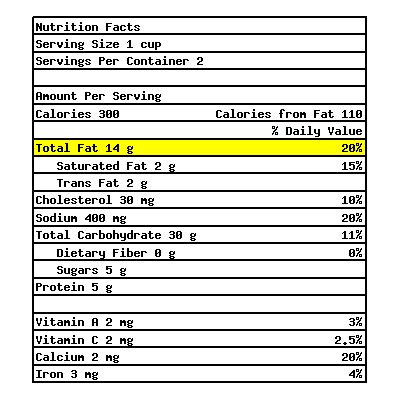
The following is a nutrition fact label from a certain macaroni and cheese box.

eps pdf png svg tex

The highlighted row means each serving of macaroni and cheese in this box contains ${14\ {\rm g}}$ of fat, which is $20\%$ of an average person’s daily intake of fat. What’s the recommended daily intake of fat for an average person?

The recommended daily intake of fat for an average person is .

55

Sydney earned ${\$278.07}$ of interest from a mutual fund, which was $0.69\%$ of his total investment. How much money did Sydney invest into this mutual fund?

Sydney invested in this mutual fund.

56

Shane earned ${\$102.81}$ of interest from a mutual fund, which was $0.23\%$ of his total investment. How much money did Shane invest into this mutual fund?

Shane invested in this mutual fund.

57

A town has $5000$ registered residents. Among them, there are $1950$ Democrats and $1750$ Republicans. The rest are Independents. What percentage of registered voters in this town are Independents?

In this town, of all registered voters are Independents.

58

A town has $1300$ registered residents. Among them, there are $468$ Democrats and $299$ Republicans. The rest are Independents. What percentage of registered voters in this town are Independents?

In this town, of all registered voters are Independents.

59

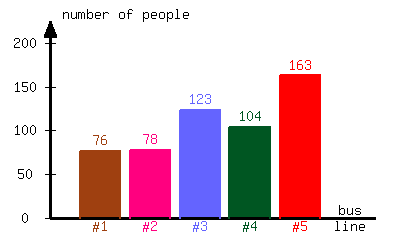
A community college conducted a survey about the number of students riding each bus line available. The following bar graph is the result of the survey.

eps pdf png svg tex

What percent of students ride Bus #1?

Approximately of students ride Bus #1.

60

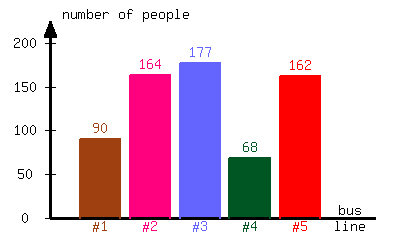
A community college conducted a survey about the number of students riding each bus line available. The following bar graph is the result of the survey.

eps pdf png svg tex

What percent of students ride Bus #1?

Approximately of students ride Bus #1.

Percent Increase/Decrease

61

The population of cats in a shelter decreased from $100$ to $75\text{.}$ What is the percentage decrease of the shelter’s cat population?

The percentage decrease is .

62

The population of cats in a shelter decreased from $120$ to $108\text{.}$ What is the percentage decrease of the shelter’s cat population?

The percentage decrease is .

63

The population of cats in a shelter increased from $55$ to $73\text{.}$ What is the percentage increase of the shelter’s cat population?

The percentage increase is approximately .

64

The population of cats in a shelter increased from $63$ to $75\text{.}$ What is the percentage increase of the shelter’s cat population?

The percentage increase is approximately .

65

Last year, a small town’s population was $760\text{.}$ This year, the population decreased to $753\text{.}$ What is the percentage decrease?

The percentage decrease of the town’s population was approximately .

66

Last year, a small town’s population was $800\text{.}$ This year, the population decreased to $798\text{.}$ What is the percentage decrease?

The percentage decrease of the town’s population was approximately .

67

Your salary used to be ${\$39{,}000}$ per year.

You had to take a $2\%$ pay cut. After the cut, your salary was per year.

Then, you earned a $2\%$ raise. After the raise, your salary was per year.

68

Your salary used to be ${\$31{,}000}$ per year.

You had to take a $2\%$ pay cut. After the cut, your salary was per year.

Then, you earned a $2\%$ raise. After the raise, your salary was per year.

69

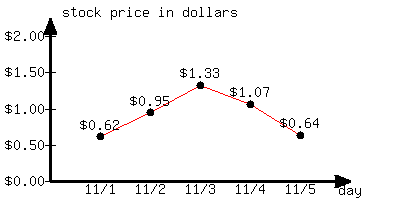
This line graph shows a certain stock's price change over a few days.

eps pdf png svg tex

From 11/1 to 11/5, what is the stock price’s percentage change?

From 11/1 to 11/5, the stock price’s percentage change was approximately .

70

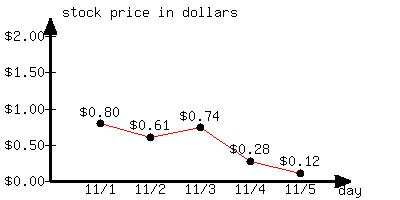
This line graph shows a certain stock's price change over a few days.

eps pdf png svg tex

From 11/1 to 11/5, what is the stock price’s percentage change?

From 11/1 to 11/5, the stock price’s percentage change was approximately .

71

A house was bought two years ago at the price of ${\$110{,}000}\text{.}$ Each year, the house’s value decreased by $5\%\text{.}$ What’s the house’s value this year?

The house’s value this year is .

72

A house was bought two years ago at the price of ${\$380{,}000}\text{.}$ Each year, the house’s value decreased by $6\%\text{.}$ What’s the house’s value this year?

The house’s value this year is .