Section 2.2 Geometry Formulas
¶Two- and three- dimensional shapes provide some formulas with variables that we can evaluate.
Subsection 2.2.1 Evaluating Perimeter and Area Formulas
¶Rectangles
The rectangle in Figure 2.2.2 has a length (as measured by the edges on the top and bottom) and a width (as measured by the edges on the left and right).
Perimeter is the distance around the edge(s) of a two-dimensional shape. To calculate perimeter, start from a point on the shape (usually a corner), travel around the shape, and add up the total distance traveled. For the rectangle in the Figure 2.2.2, if we travel around it, the total distance would be:
Another way to compute a rectangle's perimeter would be to start at one corner, add up the edge length half-way around, and then double that. So we could have calculated the perimeter this way:
There is nothing special about this rectangle having length 3 cm and width 2 cm. With a generic rectangle, it has some length we can represent with the variable \(\ell\) and some width we can represent with the variable \(w\text{.}\) We can use \(P\) to represent its perimeter, and then the perimeter of the rectangle will be given by:
Area is the number of \(1\times1\) squares that fit inside a two-dimensional shape (possibly after morphing them into non-square shapes). If the edges of the squares are, say, 1 cm long, then the area is measured in “square cm,” written cm2. In Figure 2.2.2, the rectangle has six 1 cm × 1 cm squares, so its area is \(6\) square centimeters.
Note that we can find that area by multiplying the length and the width:
Again, there is nothing special about this rectangle having length 3 cm and width 2 cm. With a generic rectangle, it has some length we can represent with the variable \(\ell\) and some width we can represent with the variable \(w\text{.}\) We can represent its area with the variable \(A\text{,}\) and then the area of the rectangle will be given by:
Checkpoint 2.2.3
Triangles
The perimeter of a general triangle has no special formula — all that is needed is to add the lengths of its three sides. The area of a triangle is a bit more interesting. In Figure 2.2.4, there are three triangles. From left to right, there is an acute triangle, a right triangle, and an obtuse triangle. Each triangle is drawn so that there is a “bottom” horizontal edge. This edge is referred to as the “base” of the triangle. With each triangle, a “height” that is perpendicular to the base is also illustrated.
Each of these triangles has the same base width, 3 cm, and the same height, 2 cm. Note that they each have the same area as well. Figure 2.2.5 illustrates how they each have an area of 3 cm2.
As with the triangles in Figure 2.2.5, you can always rearrange little pieces of a triangle so that the resulting shape is a rectangle with the same base width, but with a height that's one-half of the triangle's height. With a generic rectangle, it has some base width we can represent with the variable \(b\) and some height we can represent with the variable \(h\text{.}\) We can represent its area with the variable \(A\text{,}\) and then the area of the triangle will be given by \(A=b\cdot\left(\frac{1}{2}h\right)\text{,}\) or more conventionally:
Checkpoint 2.2.6
Circles
To find formulas for the perimeter and area of a circle, it helps to first know that there is a special number called \(\pi\) (spelled “pi” and pronounced like “pie”) that appears in many places in mathematics. The decimal value of \(\pi\) is about \(3.14159265\ldots\text{,}\) and it helps to memorize some of these digits. It also helps to understand that \(\pi\) is a little larger than \(3\text{.}\) There are many definitions for \(\pi\) that can explain where it comes from and how you can find all its decimal places, but here we are just going to accept that it is a special number, and it is roughly \(3.14159265\ldots\text{.}\)
The perimeter of a circle is the distance around its edge. For circles, the perimeter has a special name: the circumference. Imagine wrapping a string around the circle and cutting it so that it makes one complete loop. If we straighten out that piece of string, we have a length that is just as long as the circle's circumference.
As we can see in Figure 2.2.7, the circumference of a circle is a little more than three times as long as its diameter. (The diameter of a circle is the length of a straight line running from a point on the edge through the center to the opposite edge.) In fact, the circumference is actually exactly \(\pi\) times the length of the diameter. With a generic circle, it has some diameter we can represent with the variable \(d\text{.}\) We can represent its circumference with the variable \(c\text{,}\) and then the circumference of the circle will be given by:
Alternatively, we often prefer to work with a circle's radius instead of its diameter. The radius is the distance from any point on the circle's edge to its center. (Note that the radius is half the diameter.) From this perspective, we can see in Figure 2.2.8 that the circumference is a little more than \(6\) times the radius.
This gives us another formula for a circle's circumerence that uses the variable \(r\) for its radius: \(c=\pi\cdot2r\text{.}\) Or more conventionally,
There is also a formula for the area of a circle based on its radius. Figure 2.2.9 shows how three squares can be cut up and rearranged to fit inside a circle. This shows how the area of a circle of radius \(r\) is just a little larger than \(3r^2\text{.}\) Since \(\pi\) is just a little larger than \(3\text{,}\) could it be that the area of a circle is given by \(\pi r^2\text{?}\)
One way to establish this formula is to imagine slicing up the circle into many pie slices as in Figure 2.2.10. Then you can rearrange the slices into a strange shape that is almost a rectangle with height equal to the radius of the original circle, and width equal to half the circumference of the original circle.
Since the area of the circle is equal to the area of the almost-rectangular shape in Figure 2.2.10, we have the circle area formula:
Checkpoint 2.2.11
Subsection 2.2.2 Volume
The volume of a three-dimensional object is the number of \(1\times1\times1\) cubes that fit inside the object (possibly after morphing them into non-cube shapes). If the edges of the cubes are, say, 1 cm long, then the volume is measured in “cubic cm,” written cm3.
Rectangular Prisms
The 3D shape in Figure 2.2.12 is called a rectangular prism.
The rectangular prism in Figure 2.2.12 is composed of \(1\,\text{in}\times1\,\text{in}\times1\,\text{in}\) unit cubes, with each cube's volume being \(1\) cubic inch (or \(\text{in}^3\)). The shape's volume is the number of such unit cubes. The bottom face has \(5\cdot4=20\) unit squares. Since there are \(3\) layers of cubes, the shape has a total of \(3\cdot20=60\) unit cubes. In other words, the shape's volume is 60 in3 because it has sixty 1 in × 1 in × 1 in cubes inside it.
We found the number of unit squares in the bottom face by multiplying \(5\cdot4=20\text{.}\) Then to find the volume, we multiplied by \(3\) because there are three layers of cubes. So one formula for a prism's volume is
where \(V\) stands for volume, \(w\) for width, \(d\) for depth, and \(h\) for height.
Checkpoint 2.2.13
Cylinders
A cylinder is not a prism, but it has some similarities. Instead of a square base, the base is a circle. Its volume can also be calculated in a similar way to how prism volume is calculated. Let's look at an example.
Example 2.2.14
Find the volume of a cylinder with a radius of \(3\) meters and a height of \(2\) meters.
The base of the cylinder is a circle. We know the area of a circle is given by the formula \(A=\pi r^2\text{,}\) so the base area is 9\(\pi\) m2, or about 28.27 m2. That means about \(28.27\) unit squares can fit into the base. One of them is drawn in Figure 2.2.16 along with two unit cubes above it.
For each unit square in the base circle, there are two unit cubes of volume. So the volume is the base area times the height: \(9\pi\,\text{m}^2\cdot2\,\text{m}\text{,}\) which equals \(18\pi\,\text{m}^3\text{.}\) Approximating \(\pi\) with a decimal value, this is about 56.55 m3.
Example 2.2.14 demonstrates that the volume of a cylinder can be calculated with the formula
where \(r\) is the radius and \(h\) is the height.
Checkpoint 2.2.17
Note that the volume formulas for a rectangular prism and a cylinder have something in common: both formulas first find the area of the base (which is a rectangle for a prism and a circle for a cylinder) and then multiply by the height. So there is another formula
that works for both shapes. Here, \(B\) stands for the base area (which is \(wd\) for a prism and \(\pi r^2\) for a cylinder.)
Subsection 2.2.3 Summary
You may be required to memorize the geometry formulas that have been cataloged in this section. Check that you have each of them memorized here.
Checkpoint 2.2.18
Subsection 2.2.4 Exercises
Perimeter and Area
3
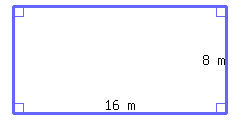
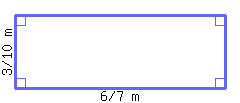
Find the perimeter of the rectangle below.
4
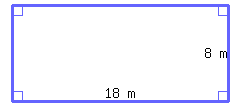
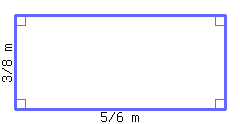
Find the perimeter of the rectangle below.
5
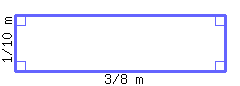
Find the area of the rectangle below.
6
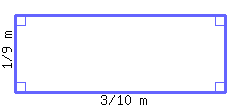
Find the area of the rectangle below.
7
Find the perimeter and area of a rectangular table top with a length of \({4\ {\rm ft}}\) and a width of \({27\ {\rm in}}\text{.}\)
Its perimeter is and its area is .
8
Find the perimeter and area of a rectangular table top with a length of \({4.2\ {\rm ft}}\) and a width of \({36\ {\rm in}}\text{.}\)
Its perimeter is and its area is .
9
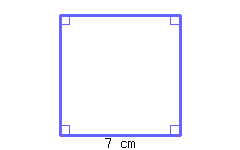
Find the perimeter and area of the square.
The square’s perimeter is .
The square’s area is .
10
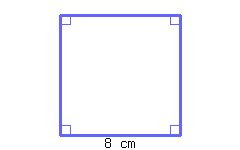
Find the perimeter and area of the square.
The square’s perimeter is .
The square’s area is .
11
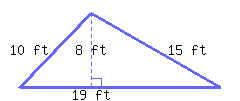
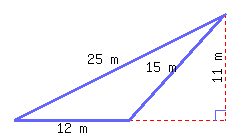
Find the perimeter and area of the triangle.
Its perimeter is and its area is .
12
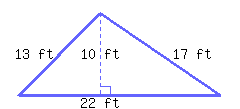
Find the perimeter and area of the triangle.
Its perimeter is and its area is .
13
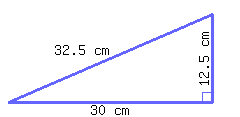
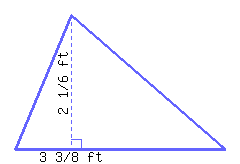
Find the perimeter and area of the right triangle.
Its perimeter is and its area is .
14
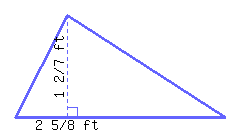
Find the perimeter and area of the right triangle.
Its perimeter is and its area is .
15
Find the perimeter and area of the triangle.
Its perimeter is and its area is .
16
Find the perimeter and area of the triangle.
Its perimeter is and its area is .
17
The area of the triangle below is square feet.
18
The area of the triangle below is square feet.
19
Find the area of a triangular flag with a base of \({2.6\ {\rm m}}\) and a height of \({60\ {\rm cm}}\text{.}\)
Its area is .
20
Find the area of a triangular flag with a base of \({2.9\ {\rm m}}\) and a height of \({130\ {\rm cm}}\text{.}\)
Its area is .
21
A circle’s radius is \({6\ {\rm m}}\text{.}\)
This circle’s circumference, in terms of \(\pi\text{,}\) is .
This circle’s circumference, rounded to the hundredth place, is .
This circle’s area, in terms of \(\pi\text{,}\) is .
This circle’s area, rounded to the hundredth place, is .
22
A circle’s radius is \({7\ {\rm m}}\text{.}\)
This circle’s circumference, in terms of \(\pi\text{,}\) is .
This circle’s circumference, rounded to the hundredth place, is .
This circle’s area, in terms of \(\pi\text{,}\) is .
This circle’s area, rounded to the hundredth place, is .
23
A circle’s diameter is \({16\ {\rm m}}\text{.}\)
This circle’s circumference, in terms of \(\pi\text{,}\) is .
This circle’s circumference, rounded to the hundredth place, is .
This circle’s area, in terms of \(\pi\text{,}\) is .
This circle’s area, rounded to the hundredth place, is .
24
A circle’s diameter is \({18\ {\rm m}}\text{.}\)
This circle’s circumference, in terms of \(\pi\text{,}\) is .
This circle’s circumference, rounded to the hundredth place, is .
This circle’s area, in terms of \(\pi\text{,}\) is .
This circle’s area, rounded to the hundredth place, is .
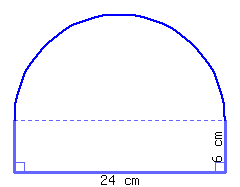
25
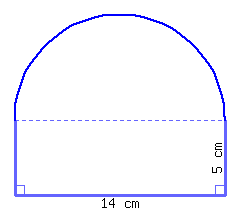
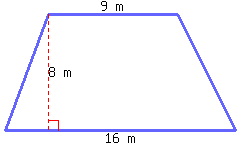
Find the perimeter and area of this shape, which is a semicircle on top of a rectangle.
Its perimeter is and its area is .
26
Find the perimeter and area of this shape, which is a semicircle on top of a rectangle.
Its perimeter is and its area is .
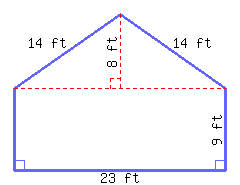
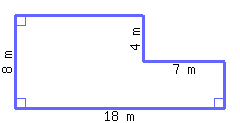
27
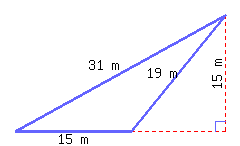
Find the perimeter and area of this polygon.
Its perimeter is and its area is .
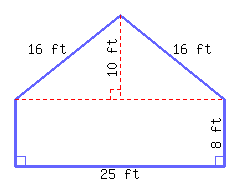
28
Find the perimeter and area of this polygon.
Its perimeter is and its area is .
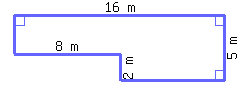
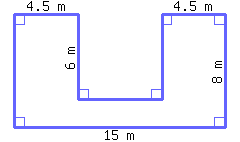
29
Find the perimeter and area of this shape.
Its perimeter is and its area is .
30
Find the perimeter and area of this shape.
Its perimeter is and its area is .
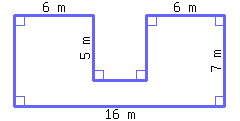
31
Find the perimeter and area of this polygon.
Its perimeter is and its area is .
32
Find the perimeter and area of this polygon.
Its perimeter is and its area is .
33
The formula
gives the area of a regular polygon with side length \(s\text{,}\) number of sides \(n\) and, apothem \(r\text{.}\) (The apothem is the distance from the center of the polygon to one of its sides.)
What is the area of a regular pentagon with \(s= {90\ {\rm in}}\) and \(r={82\ {\rm in}}\text{?}\)
The area is .
34
The formula
gives the area of a regular polygon with side length \(s\text{,}\) number of sides \(n\) and, apothem \(r\text{.}\) (The apothem is the distance from the center of the polygon to one of its sides.)
What is the area of a regular \(28\)-gon with \(s= {99\ {\rm in}}\) and \(r={90\ {\rm in}}\text{?}\)
The area is .
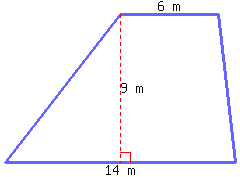
35
A trapezoid’s area can be calculated by the formula \(A=\frac{1}{2}(b_1+b_2)h\text{,}\) where \(A\) stands for area, \(b_1\) for the first base’s length, \(b_2\) for the second base’s length, and \(h\) for height.
Find the area of the trapezoid below.
36
A trapezoid’s area can be calculated by the formula \(A=\frac{1}{2}(b_1+b_2)h\text{,}\) where \(A\) stands for area, \(b_1\) for the first base’s length, \(b_2\) for the second base’s length, and \(h\) for height.
Find the area of the trapezoid below.
Volume
37
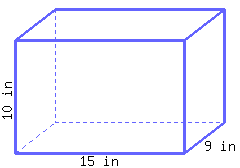
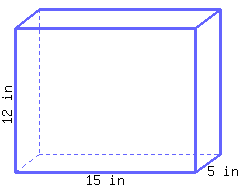
Find the volume of this rectangular prism.
38
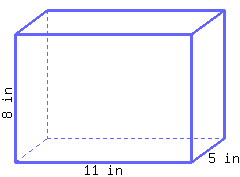
Find the volume of this rectangular prism.
39
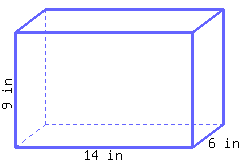
Find the volume of this rectangular prism.
40
Find the volume of this rectangular prism.
41
A cube’s side length is \({8\ {\rm cm}}\text{.}\) Its volume is .
42
A cube’s side length is \({9\ {\rm cm}}\text{.}\) Its volume is .
43
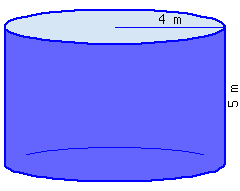
Find the volume of this cylinder.
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
44
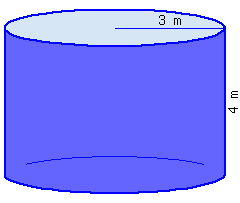
Find the volume of this cylinder.
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
45
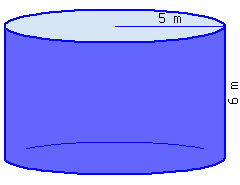
Find the volume of this cylinder.
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
46
Find the volume of this cylinder.
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
47
A cylinder’s base’s diameter is \({10\ {\rm ft}}\text{,}\) and its height is \({5\ {\rm ft}}\text{.}\)
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
48
A cylinder’s base’s diameter is \({4\ {\rm ft}}\text{,}\) and its height is \({6\ {\rm ft}}\text{.}\)
This cylinder’s volume, in terms of \(\pi\text{,}\) is .
This cylinder’s volume, rounded to the hundredth place, is .
49
The formula \(V=\frac{1}{3}\cdot s^2\cdot h\) gives the volume of a right square pyramid.
What is the volume of a right square pyramid with \(s= {66\ {\rm in}}\) and \(h={69\ {\rm in}}\text{?}\)
50
The formula \(V=\frac{1}{3}\cdot s^2\cdot h\) gives the volume of a right square pyramid.
What is the volume of a right square pyramid with \(s= {78\ {\rm in}}\) and \(h={34\ {\rm in}}\text{?}\)