41
Does the following set of ordered pairs make for a function of \(x\text{?}\)
\(\Big\{(9,2),(5,8),(8,6),(-3,3),(-5,9)\Big\}\)
This set of ordered pairs
describes
does not describe
a function of \(x\text{.}\) This set of ordered pairs has domain and range .
42
Does the following set of ordered pairs make for a function of \(x\text{?}\)
\(\Big\{(5,8),(-6,5),(10,4),(-6,10),(-7,5)\Big\}\)
This set of ordered pairs
describes
does not describe
a function of \(x\text{.}\) This set of ordered pairs has domain and range .
43
Below is all of the information that exists about a function \(f\text{.}\)
\(\begin{aligned}
f(0)\amp =2\amp
f(2)\amp =2\amp
f(3)\amp =2
\end{aligned}\)
Write \(f\) as a set of ordered pairs.
\(f\) has domain and range .
44
Below is all of the information about a function \(g\text{.}\)
\(\begin{aligned}
g(a)\amp =1\amp
g(b)\amp =5\\
g(c)\amp =-5\amp
g(d)\amp =5
\end{aligned}\)
Write \(g\) as a set of ordered pairs.
\(g\) has domain and range .
45
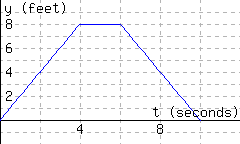
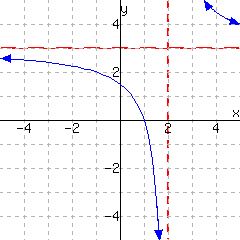
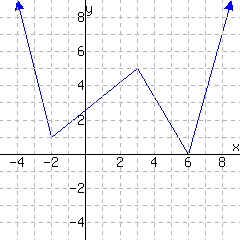
The following graphs show two relationships. Decide whether each graph shows a relationship where \(y\) is a function of \(x\text{.}\)
The first graph
give a function of \(x\text{.}\) The second graph give a function of \(x\text{.}\)
46
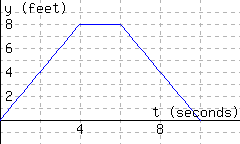
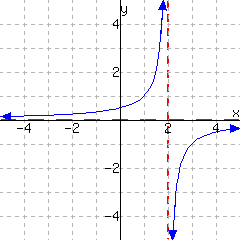
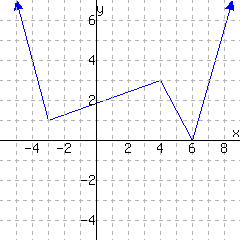
The following graphs show two relationships. Decide whether each graph shows a relationship where \(y\) is a function of \(x\text{.}\)
The first graph
give a function of \(x\text{.}\) The second graph give a function of \(x\text{.}\)
47
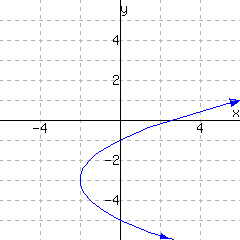
Some equations involving \(x\) and \(y\) define \(y\) as a function of \(x\text{,}\) and others do not. For example, if \(x+y=1\text{,}\) we can solve for \(y\) and obtain \(y = 1-x\text{.}\) And we can then think of \(y = f(x) =
1-x\text{.}\) On the other hand, if we have the equation \(x=y^2\) then \(y\) is not a function of \(x\text{,}\) since for a given positive value of \(x\text{,}\) the value of \(y\) could equal \(\sqrt{x}\) or it could equal \(-\sqrt{x}\text{.}\)
Select all of the following relations that make \(y\) a function of \(x\). There are several correct answers.
On the other hand, some equations involving \(x\) and \(y\) define \(x\) as a function of \(y\) (the other way round).
Select all of the following relations that make \(x\) a function of \(y\). There are several correct answers.
48
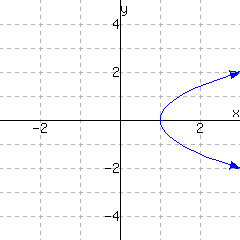
Some equations involving \(x\) and \(y\) define \(y\) as a function of \(x\text{,}\) and others do not. For example, if \(x+y=1\text{,}\) we can solve for \(y\) and obtain \(y = 1-x\text{.}\) And we can then think of \(y = f(x) =
1-x\text{.}\) On the other hand, if we have the equation \(x=y^2\) then \(y\) is not a function of \(x\text{,}\) since for a given positive value of \(x\text{,}\) the value of \(y\) could equal \(\sqrt{x}\) or it could equal \(-\sqrt{x}\text{.}\)
Select all of the following relations that make \(y\) a function of \(x\). There are several correct answers.
On the other hand, some equations involving \(x\) and \(y\) define \(x\) as a function of \(y\) (the other way round).
Select all of the following relations that make \(x\) a function of \(y\). There are several correct answers.
49
Determine whether or not the following table could be the table of values of a function. If the table can not be the table of values of a function, give an input that has more than one possible output.
| Input |
Output |
| \(2\) |
\(9\) |
| \(4\) |
\(-5\) |
| \(6\) |
\(9\) |
| \(8\) |
\(5\) |
| \(-2\) |
\(-8\) |
Could this be the table of values for a function?
If not, which input has more than one possible output?
50
Determine whether or not the following table could be the table of values of a function. If the table can not be the table of values of a function, give an input that has more than one possible output.
| Input |
Output |
| \(2\) |
\(13\) |
| \(4\) |
\(-19\) |
| \(6\) |
\(-15\) |
| \(8\) |
\(-7\) |
| \(-2\) |
\(-9\) |
Could this be the table of values for a function?
If not, which input has more than one possible output?
51
Determine whether or not the following table could be the table of values of a function. If the table can not be the table of values of a function, give an input that has more than one possible output.
| Input |
Output |
| \(-4\) |
\(7\) |
| \(-3\) |
\(-4\) |
| \(-2\) |
\(-5\) |
| \(-3\) |
\(13\) |
| \(-1\) |
\(-3\) |
Could this be the table of values for a function?
If not, which input has more than one possible output?
52
Determine whether or not the following table could be the table of values of a function. If the table can not be the table of values of a function, give an input that has more than one possible output.
| Input |
Output |
| \(-4\) |
\(-14\) |
| \(-3\) |
\(-2\) |
| \(-2\) |
\(12\) |
| \(-3\) |
\(19\) |
| \(-1\) |
\(15\) |
Could this be the table of values for a function?
If not, which input has more than one possible output?