1
Use technology to make a table of values for the function \(K\) defined by \(K(x)={3x^{2}-2x-3}\text{.}\)
2
Use technology to make a table of values for the function \(f\) defined by \(f(x)={-3x^{2}-8x+37}\text{.}\)
3
Use technology to make a graph of \(f\) where \(f(x)=3x^2-6x-5\text{.}\)
4
Use technology to make a graph of \(f\) where \(f(x)=-3x^2-8x+3\text{.}\)
5
Let \(g(x)={-x^{2}+x+3}\text{.}\) Use technology to find the following.
The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .
The domain of \(g\) is .
The range of \(g\) is .
Calculate \(g(3)\text{.}\) .
Solve \(g(x)=2\text{.}\)
Solve \(g(x)>2\text{.}\)
6
Let \(h(x)={-x^{2}-4x-2}\text{.}\) Use technology to find the following.
The vertex is .
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .
The domain of \(h\) is .
The range of \(h\) is .
Calculate \(h(-1)\text{.}\) .
Solve \(h(x)=-5\text{.}\)
Solve \(h(x)\geq-5\text{.}\)
7
An object was launched from the top of a hill with an upward vertical velocity of \(110\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+110t+200}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Find the answer using technology.
seconds after its launch, the object reached its maximum height of feet.
8
An object was launched from the top of a hill with an upward vertical velocity of \(130\) feet per second. The height of the object can be modeled by the function \(h(t)={-16t^{2}+130t+100}\text{,}\) where \(t\) represents the number of seconds after the launch. Assume the object landed on the ground at sea level. Find the answer using technology.
seconds after its launch, the object fell to the ground at sea level.
9
Find the vertex of the graph of
\begin{equation*}
y=3\!\left(x-7\right)^{2}-6
\end{equation*}
10
Find the vertex of the graph of
\begin{equation*}
y=6\!\left(x-3\right)^{2}-3
\end{equation*}
11
Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((-7,-8)\) and has leading coefficient \(a=7\text{.}\)
\(\displaystyle{ f(x) =}\)
12
Write the vertex form for the quadratic function \(f\text{,}\) whose vertex is \((6,6)\) and has leading coefficient \(a=9\text{.}\)
\(\displaystyle{ f(x) =}\)
13
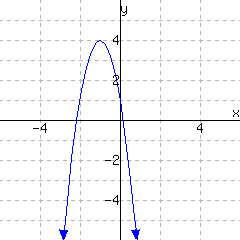
A graph of a function \(f\) is given. Use the graph to write a formula for \(f\) in vertex form. You will need to identify the vertex and also one more point on the graph to find the leading coefficient \(a\text{.}\)
\(\displaystyle{ f(x) =}\)
14
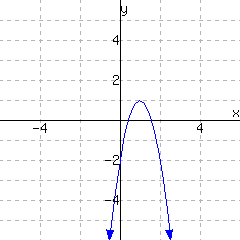
A graph of a function \(f\) is given. Use the graph to write a formula for \(f\) in vertex form. You will need to identify the vertex and also one more point on the graph to find the leading coefficient \(a\text{.}\)
\(\displaystyle{ f(x) =}\)
15
Let \(h\) be defined by \(h(x)={\left(x-5\right)^{2}+5}\text{.}\)
What is the domain of \(h\text{?}\)
What is the range of \(h\text{?}\)
16
Let \(h\) be defined by \(h(x)={\left(x+2\right)^{2}-7}\text{.}\)
What is the domain of \(h\text{?}\)
What is the range of \(h\text{?}\)
17
Consider the graph of the equation \(y={\left(x-1\right)^{2}-8}\text{.}\)
Compared to the graph of \(y=x^2\text{,}\) the vertex has been shifted units
and units .
18
Consider the graph of the equation \(y={\left(x-3\right)^{2}+4}\text{.}\)
Compared to the graph of \(y=x^2\text{,}\) the vertex has been shifted units
and units .
19
The quadratic expression \({\left(x-4\right)^{2}-4}\) is written in vertex form.
Write the expression in standard form.
Write the expression in factored form.
20
The quadratic expression \({\left(x-4\right)^{2}-1}\) is written in vertex form.
Write the expression in standard form.
Write the expression in factored form.
21
The formula for a quadratic function \(g\) is \(g(x)={\left(x-9\right)\!\left(x-3\right)}\text{.}\)
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .
22
The formula for a quadratic function \(G\) is \(G(x)={\left(x+8\right)\!\left(x+3\right)}\text{.}\)
The \(y\)-intercept is .
The \(x\)-intercept(s) is/are .