ORCCAOpen Resources for Community College Algebra

Since Monday has an arrow to \(0.2\text{,}\) that must mean that it rained \(0.2\) inches of rain on Monday. That gives us the ordered pair \((\text{Monday},0.2)\text{.}\) Likewise, we also have \((\text{Tuesday},0.4)\text{.}\) To write down all of the ordered pairs, we will use a set:

Yes, that relation was a function. If I tell you the day of the week, you can with certainty “predict” how much rain there was on that day by looking at the data. There was a single answer to the question “How much rain fell on Wednesday during that week in Portland?”

At this point, we should note that all historical weather data can be viewed as a function of some sort: On any particular day in the recent past, we can “predict” (by looking it up somewhere) how much rain fell in any city in the world.

However, the opposite question, “If it rained \(0.0\) inches, what day of the year was it?” is not going to represent a function because there will be more than one day of the year that it didn't rain at all. Even in Portland.

1. This question is equivalent to the question “If you input any \(x\) value, will there be only one \(y\) value?” The answer is “yes.” If you input any number for \(x\) you first square that number and multiply it by two, then add the number. For example, if we substitute \(\substitute{-3}\text{,}\) we get:

   \begin{align*} y\amp=2(\substitute{x})^2+(\substitute{x})\\ y\amp=2(\substitute{-3})^2+(\substitute{-3})\\ \amp=2(9)-3\\ \amp=18-3\\ \amp=15 \end{align*}

   There is no way we could substitute a number for \(x\) and get more than one value for \(y\text{.}\)

2. This question is equivalent to the question “If you input any \(x\) value, will there be only one \(y\) value?” The answer is “no.” If you input any number for \(x\) and solve for \(y\text{,}\) you might actually get two solutions. For example, if we substitute \(\substitute{1}\text{,}\) we get:

   \begin{align*} y^2\amp=\substitute{x}\\ y^2\amp=\substitute{1} \end{align*}
   \begin{align*} y\amp=\sqrt{1}\amp\text{ or }\amp\amp y\amp=-\sqrt{1}\\ y\amp=1\amp\text{ or }\amp\amp y\amp=-1 \end{align*}

   Since there is more than one \(y\) value for the \(x\) value \(1\text{,}\) the relation \(y^2=x\) is not a function.

For the function \(V=g(x)\text{,}\) the name of the function is \(g\text{,}\) the input variable is \(x\text{,}\) and the output variable is \(V\text{.}\)

1. To evaluate \(a(-3)\) we will substitute the value \(\substitute{-3}\) in wherever we see \(x\) in the equation for \(a(x)\text{.}\)

   \begin{align*} a(\substitute{x})\amp=\substitute{x}^2-2\substitute{x}\\ a(\substitute{-3})\amp=(\substitute{-3})^2-2(\substitute{-3})\\ \amp=9+6\\ \amp=15 \end{align*}

2. To evaluate \(b(-3)\text{,}\) we need to look at the graph of \(y=b(x)\) and look for the one place on the graph where the \(x\)-value is \(-3\text{.}\) The \(y\)-value at this point is \(1\text{,}\) so we would say that

   \begin{equation*} b(-3)=1 \end{equation*}

3. To evaluate \(c(-3)\) we examine the table and find the place where the \(x\)-value is \(-3\text{.}\) We conclude that \(c(-3)=-2\text{.}\)

1. To solve the equation \(a(x)=0\text{,}\) we should set the formula for \(a(x)\) equal to \(0\text{.}\) In this case, factoring will then help.

   \begin{align*} x^2-2x\amp=0\\ x(x-2)\amp=0 \end{align*}
   \begin{align*} x\amp=0\amp\text{ or }\amp\amp x-2\amp=0\\ x\amp=0\amp\text{ or }\amp\amp x\amp=2 \end{align*}

   So, the solution set is \(\{0,2\}\text{.}\)

2. To solve the equation \(b(x)=2\text{,}\) we should examine the graph and find all of the locations where the \(y\)-value is \(2\text{.}\) According to the graph, that happens twice, both when \(x=-4\) and when \(x=0\text{.}\) So the solution set is \(\{-4,0\}.\)

3. To solve the equation \(c(x)=7\text{,}\) we examine the table and find all the places where the function value is \(7\text{.}\) According to the table, that happens twice: once when \(x=-5\) and again when \(x=9\text{.}\) So the solution set is \(\{-5,9\}\text{.}\)

Recall the definitions of domain and range.

1. To find the the domain of \(b\text{,}\) look at the graph of \(b\) and see what \(x\)-values are used for the graph. In other words, what \(x\)-values could you input and expect to get a \(y\)-value? It looks like the graph extends forever to the right as well as the left. Therefore, the domain is \((-\infty,\infty)\text{.}\)

2. To find the the domain of \(c\text{,}\) we list the \(x\)-values in the table in a set. That would be \(\{-5,-3,2,6,9\}\text{.}\)

3. To find the the range of \(b\text{,}\) look at the graph of \(b\) and see what \(y\)-values are on the graph. The lowest \(y\)-value is \(-3\) and all higher \(y\)-values are possible outputs. Therefore, the range is \([-3,\infty)\text{.}\)

4. To find the the range of \(c\text{,}\) we list the \(y\)-values in the table in a set. That would be \(\{7,-2,2,4\}\text{.}\)

The graph in Figure 9.4.16 fails the vertical line test and so \(y\) is not a function of \(x\text{.}\) The graph in Figure 9.4.17 passes the vertical line test and so \(y\) is a function of \(x\text{.}\)

To find the vertex of a parabola algebraically, we use the formula \(h=-\frac{b}{2a}\) to find the axis of symmetry first. For our equation, \(\substitute{a=3}\) and \(\lighthigh{b=8}\text{,}\) so:

Next, we evaluate \(f\mathopen{}\left(\substitute{-\frac{4}{3}}\right)\mathclose{}\) to find the \(y\)-coordinate of the vertex.

So, the parabola has its axis of symmetry at \(x=-\frac{4}{3}\) and has its vertex at the point \(\left(-\frac{4}{3},-\frac{37}{3}\right)\text{.}\)

To determine the vertex of \(g(x)=2x^2+8x+2\text{,}\) we want to find the \(x\)-value of the vertex first. We will use \(h=-\frac{b}{2a}\) for \(\substitute{a=2}\) and \(\lighthigh{b=8}\text{:}\)

To find the vertex, we evaluate \(g(\substitute{-2})\text{.}\)

Now we know that our axis of symmetry is the line \(x=-2\) and the vertex is the point \((-2,-6)\text{.}\) We will set up our table with two values on each side of \(x=-2\text{.}\) We choose \(x= -4, -3, \highlight{-2}, -1,\) and \(0\text{.}\) Then, we'll determine the \(y\)-coordinates by replacing \(x\) with each value and we have the complete table as shown in Table 9.4.23. Notice that each pair of \(y\)-values on either side of the vertex match. This helps us to check that our vertex and \(y\)-values are correct.

Now that we have our table, we will plot the points and draw in the axis of symmetry as shown in Figure 9.4.24. We complete the graph by drawing a smooth curve through the points and drawing an arrow on each end as shown in Figure 9.4.25

epspdfpngsvgtex

epspdfpngsvgtex

For the domain, we look horizontally and see the graph is a continuous curve and one arrow points to the left and the other arrow points to the right. The domain is \(\{x\mid x\ \textrm{is a real number}\}\) which is equivalent to \((-\infty,\infty)\text{.}\)

For the range we look up and down on the graph, which opens upward. Both arrows point upward and the lowest point on the graph is the vertex at the point \((-2,-6)\text{.}\) The range is \(\{y \mid y \ge -6\}\) which is equivalent to \([-6,\infty)\text{.}\)

To find the vertex of \(F(x)=-0.07x^2+2.7x+248\text{,}\) we first find the axis of symmetry using the formula \(h=-\frac{b}{2a}\text{.}\) For our equation, \(\substitute{a=-0.07}\) and \(\lighthigh{b=2.7}\text{,}\) so:

Next, we substitute the value of the axis of symmetry, \(\substitute{19.3}\text{,}\) into the formula for the parabola.

So, the parabola has its axis of symmetry at \(x=19.3\) and has its vertex at about the point \((19.3,274)\text{.}\) In addition, since \(a=-0.07\text{,}\) the parabola will be opening downward. Given this information, the vertex of this parabola is its maximum.

In the reality of the situation, the \(19.3\) indicates the number of days after December 28, 2017 which would be sometime on January 16. The \(274\) indicates the stock price in dollars. In conclusion, FedEx's stock peaked (between December 28, 2017 and February 9, 2018) on January 16 at a value of \(\$274\text{.}\)

1. To find the vertical intercept, we evaluate the function when \(x=0\text{.}\)

   \begin{align*} h(\substitute{0})\amp=6(\substitute{0})^2-13(\substitute{0})+6\\ \amp=6 \end{align*}

   So, the vertical intercept of \(h\) is \((0,6)\text{.}\)

   Next, to find the horizontal intercepts, we set the function equal to zero. To solve that equation we will use Algorithm 8.6.2. For this particular example, we will practice factoring using the AC method. Here, \(ac=36\) and factor pairs that add up to \(-13\) are \(-9\) and \(-4\text{,}\) as you will see.

   \begin{align*} \substitute{h(x)}\amp=6x^2-13x+6\\ \substitute{0}\amp=6x^2\mathbin{\highlight{-}}\mathbin{\highlight{13x}}+6\\ 0\amp=6x^2\mathbin{\highlight{-}}\mathbin{\highlight{9x}}\mathbin{\highlight{-}}\mathbin{\highlight{4x}}+6\\ 0\amp=3x\highlight{(2x-3)}-2\highlight{(2x-3)}\\ 0\amp=(3x-2)\highlight{(2x-3)} \end{align*}
   \begin{align*} 0\amp=3x-2\amp\text{ or }\amp\amp0\amp=2x-3\\ x\amp=\frac{2}{3}\amp\text{ or }\amp\amp x\amp=\frac{3}{2} \end{align*}

   So, the horizontal intercepts are \(\left(\frac{2}{3},0\right)\) and \(\left(\frac{3}{2},0\right)\text{.}\)

2. To find the vertical intercept, we have to evaluate the function when \(x=0\text{.}\)

   \begin{align*} k(\substitute{0})\amp=2(\substitute{0})^2-2(\substitute{0})-5\\ \amp=-5 \end{align*}

   So, the vertical intercept of \(k\) is \((0,-5)\text{.}\)

   Next, to find the horizontal intercepts, we set the function equal to zero. To solve that equation we will use Algorithm 8.6.2. For this particular example, we will use the quadratic formula because the square root method will not work (because there is a linear term) and factoring fails.

   \begin{align*} \substitute{k(x)}\amp=2x^2-2x-5\\ \substitute{0}\amp=2x^2-2x-5\\ \end{align*}

   We identify that \(\substitute{a=2}\text{,}\) \(\lighthigh{b=-2}\text{,}\) and \(c=-5\)

   \begin{align*} x\amp=\frac{-\lighthigh{b}\pm\sqrt{\lighthigh{b}^2-4\substitute{a}c}}{2\substitute{a}}\\ x\amp=\frac{-(\lighthigh{-2})\pm\sqrt{(\lighthigh{-2})^2-4(\substitute{2})(-5)}}{2(\substitute{2})}\\ x\amp=\frac{2\pm\sqrt{4+40}}{4}\\ x\amp=\frac{2\pm\sqrt{44}}{4}\\ x\amp=\frac{2\pm\sqrt{\highlight{4}\cdot11}}{4}\\ x\amp=\frac{2\pm\highlight{2}\sqrt{11}}{4}\\ x\amp=\frac{2}{4}\pm\frac{2\sqrt{11}}{4}\\ x\amp=\frac{1}{2}\pm\frac{\sqrt{11}}{2}\\ x\amp=\frac{1\pm\sqrt{11}}{2} \end{align*}

   So, the horizontal intercepts are \(\left(\frac{1+\sqrt{11}}{2},0\right)\) and \(\left(\frac{1-\sqrt{11}}{2},0\right)\text{.}\) If you wanted to graph these points, you would need to approximate them as \(\left(2.16,0\right)\) and \(\left(-1.16,0\right)\text{.}\)

To start, we'll note that this function will open downward, as the leading coefficient is negative.

To find the \(y\)-intercept, we'll evaluate \(j(0)\text{:}\)

The \(y\)-intercept is \((0,8)\text{.}\)

Next, we'll find the horizontal intercepts by setting \(j(x)=0\) and solving for \(x\text{:}\)

The \(x\)-intercepts are \((4,0)\) and \((-1,0)\text{.}\)

Lastly, we'll determine the vertex. Noting that \(\substitute{a=-2}\) and \(\lighthigh{b=6}\text{,}\) we have:

Using the \(x\)-value \(\substitute{1.5}\) to find the \(y\)-coordinate, we have:

The vertex is the point \((1.5,12.5)\text{,}\) and the axis of symmetry is the line \(x=1.5\text{.}\)

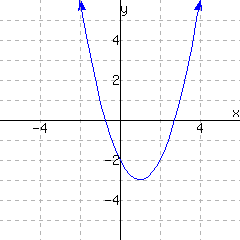
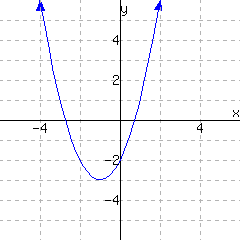
We're now ready to graph this function. We'll start by drawing and scaling the axes so all of our key features will be displayed as shown in Figure 9.4.30. Next, we'll plot these key points as shown in Figure 9.4.31. Finally, we'll note that this parabola opens downward and connect these points with a smooth curve, as shown in Figure 9.4.32.

epspdfpngsvgtex

epspdfpngsvgtex

epspdfpngsvgtex

1. The vertical intercept is found when \(\substitute{x=0}\text{.}\)

   \begin{align*} h(\substitute{x})\amp=0.0018\substitute{x}^2-0.9\substitute{x}\\ h(\substitute{0})\amp=0.0018(\substitute{0})^2-0.9(\substitute{0})\\ \amp=0 \end{align*}

   So the vertical intercept is \((0,0)\) which means that the ball was released \(0\) meters from the rim (on the rim) at a height of \(0\) meters above the rim (again, on the rim).

2. The horizontal intercepts are found when \(h(x)=0\text{.}\) This will be a quadratic equation that we can solve using factoring.

   \begin{align*} h(x)\amp=0\\ 0.0018x^2-0.9x\amp=0\\ x\left(0.0018x-0.9\right)\amp=0 \end{align*}
   \begin{align*} x\amp=0\amp\text{ or }\amp\amp 0.0018x-0.9\amp=0\\ x\amp=0\amp\text{ or }\amp\amp 0.0018x\amp=0.9\\ x\amp=0\amp\text{ or }\amp\amp x\amp=500 \end{align*}

   The horizontal intercepts are \((0,0)\) and \((500,0)\text{.}\) The interpretation of \((0,0)\) is the same as before. The interpretation of \((500,0)\) is that the other side of the rim of the dish is \(500\) meters away. If the ball were to somehow roll all the way down, and then back up the other side, it would pop up at the opposite rim exactly \(500\) meters horizontally away.

3. The vertex is found when the \(x\)-value is at the axis of symmetry. To find that, we use the formula \(x=-\frac{\lighthigh{b}}{2\substitute{a}}\) where \(\substitute{a=0.0018}\) and \(\lighthigh{b=-0.9}\)

   \begin{align*} x\amp=-\frac{\lighthigh{b}}{2\substitute{a}}\\ x\amp=-\frac{\lighthigh{-0.9}}{2(\substitute{0.0018})}\\ \amp=250 \end{align*}

   Then, to find the \(y\)-value, we substitute that \(x\)-value, \(\substitute{250}\) into the original function.

   \begin{align*} h(\substitute{x})\amp=0.0018\substitute{x}^2-0.9\substitute{x}\\ h(\substitute{250})\amp=0.0018(\substitute{250})^2-0.9(\substitute{250})\\ \amp=-112.5 \end{align*}

   The vertex is the point \((250,-112.5)\text{.}\) Since the vale of \(a\) is positive, we know that this parabola opens upward. This means that the vertex is the lowest point on the graph. So the lowest point of the telescope dish is \(250\) meters from the rim (horizontally) and \(112.5\) meters below the height of the rim. That is one big dish!

Real world domain and range problems are sometimes subjective. The domain in this case would represent all possible \(x\)-values that make sense in the reality of the situation. Recall that \(x\) is the horizontal distance from the rim of the dish where the ball was released, in meters. Since we found out that the dish is \(500\) meters across we could say that the domain is \([0,500]\text{.}\)

The range will represent all possible \(y\) values, that make sense in reality. Recall that \(h(x)\) is the height above above the rim, in meters. Since the ball won't roll any higher than the rim of the dish, \(0\) will be the largest \(y\)-value. We found out that the lowest point on the graph is \(-112.5\) meters below the rim. So the range is [-112.5,0].

epspdfpngsvgtex

Recall that Definition 9.2.2 says that a quadratic function has the form \(f(x)=ax^2+bx+c\) where \(a\text{,}\) \(b\text{,}\) and \(c\) are real numbers, and \(a \neq 0\text{.}\)

1. The equation \(y-1=3(x-2)-5\) is not quadratic. It is in fact a linear equation.

2. The equation \(y=3(x-2)^2-5\) is quadratic. We could simplify the right hand side and would have something of the form \(y=ax^2+bx+c\text{.}\)

3. The equation \(y=\sqrt{x-2}-5\) is not quadratic. The \(x\) is inside a radical, not squared, so it cannot be converted into the form \(y=ax^2+bx+c\text{.}\)

4. The equation \(y^2=x^2-5\) is not quadratic. It cannot be re-written in the form \(y=ax^2+bx+c\) (due to the \(y^2\) term).