Section 3.5 Random variables
¶The chance of landing on single number in the game of roulette is 1/38 and the pay is 35:1. The chance of landing on Red is 18/38 and the pay is 1:1. Which game has the higher expected value? The higher standard deviation of expected winnings? How do we interpret these quantities in this context? If you were to play each game 20 times, what would the distribution of possible outcomes look like? In this section, we define and summarize random variables such as this, and we look at some of their properties.
Subsection 3.5.1 Learning objectives
Define a probability distribution and what makes a distribution a valid probability distribution.
Summarize a discrete probability distribution graphically using a histogram and verbally with respect to center, spread, and shape.
Calculate and interpret the mean (expected value) and standard deviation of a random variable.
Calculate the mean and standard deviation of a transformed random variable.
Calculate the mean of the sum or difference of random variables.
Calculate the standard deviation of the sum or difference of random variables when those variables are independent.
Subsection 3.5.2 Introduction to expected value
Example 3.5.1.
Two books are assigned for a statistics class: a textbook and its corresponding study guide. The university bookstore determined 20% of enrolled students do not buy either book, 55% buy the textbook only, and 25% buy both books, and these percentages are relatively constant from one term to another. If there are 100 students enrolled, how many books should the bookstore expect to sell to this class?
Around 20 students will not buy either book (0 books total), about 55 will buy one book (55 books total), and approximately 25 will buy two books (totaling 50 books for these 25 students). The bookstore should expect to sell about 105 books for this class.
Checkpoint 3.5.2.
Would you be surprised if the bookstore sold slightly more or less than 105 books? 1
Example 3.5.3.
The textbook costs $137 and the study guide $33. How much revenue should the bookstore expect from this class of 100 students?
About 55 students will just buy a textbook, providing revenue of
The roughly 25 students who buy both the textbook and the study guide would pay a total of
Thus, the bookstore should expect to generate about \($7,535 + $4,250 = $11,785\) from these 100 students for this one class. However, there might be some sampling variability so the actual amount may differ by a little bit.
Example 3.5.5.
What is the average revenue per student for this course?
The expected total revenue is $11,785, and there are 100 students. Therefore the expected revenue per student is \($11,785/100 = $117.85\text{.}\)
Subsection 3.5.3 Probability distributions
A probability distribution is a table of all disjoint outcomes and their associated probabilities. Table 3.5.7 shows the probability distribution for the sum of two dice.
Rules for probability distributions.
A probability distribution is a list of the possible outcomes with corresponding probabilities that satisfies three rules:
The outcomes listed must be disjoint.
Each probability must be between 0 and 1.
The probabilities must total 1.
Checkpoint 3.5.6.
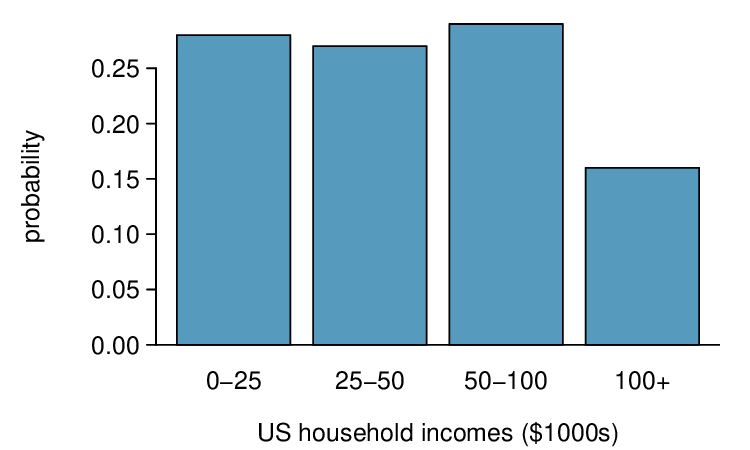
Table 3.5.8 suggests three distributions for household income in the United States. Only one is correct. Which one must it be? What is wrong with the other two? 2
| Dice | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Probability | \(\frac{1}{36}\) | \(\frac{2}{36}\) | \(\frac{3}{36}\) | \(\frac{4}{36}\) | \(\frac{5}{36}\) | \(\frac{6}{36}\) | \(\frac{5}{36}\) | \(\frac{4}{36}\) | \(\frac{3}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) |
| Income range ($1000s) | 0-25 | 25-50 | 50-100 | 100+ |
| (a) | 0.18 | 0.39 | 0.33 | 0.16 |
| (b) | 0.38 | -0.27 | 0.52 | 0.37 |
| (c) | 0.28 | 0.27 | 0.29 | 0.16 |
Chapter 2 emphasized the importance of plotting data to provide quick summaries. Probability distributions can also be summarized in a histogram or bar plot. The probability distribution for the sum of two dice is shown in Table 3.5.7 and its histogram is plotted in Figure 3.5.9. The distribution of US household incomes is shown in Figure 3.5.10 as a bar plot. The presence of the 100+ category makes it difficult to represent it with a regular histogram. 3
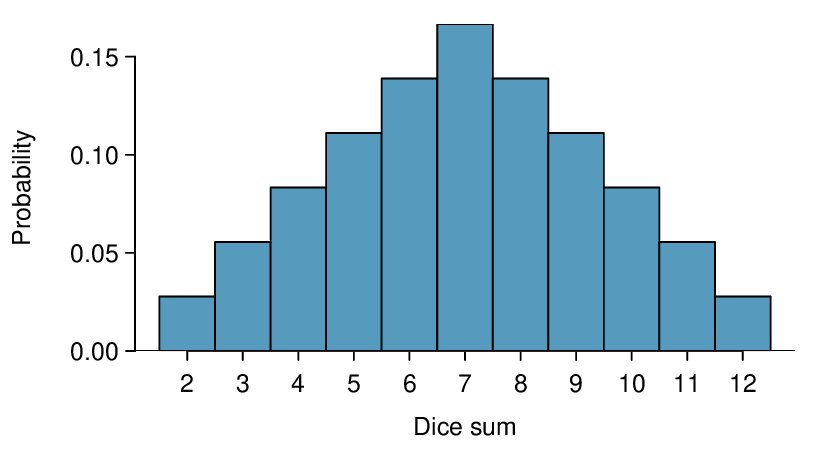
In these bar plots, the bar heights represent the probabilities of outcomes. If the outcomes are numerical and discrete, it is usually (visually) convenient to make a histogram, as in the case of the sum of two dice. Another example of plotting the bars at their respective locations is shown in Figure 3.5.4.
Subsection 3.5.4 Expectation
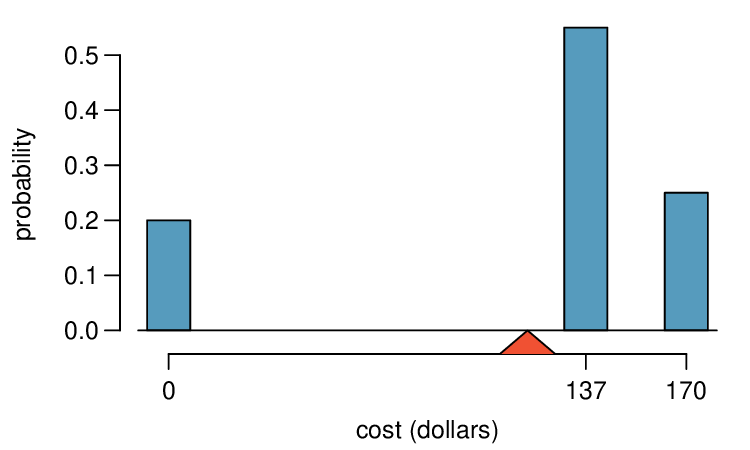
We call a variable or process with a numerical outcome a random variable, and we usually represent this random variable with a capital letter such as \(X\text{,}\) \(Y\text{,}\) or \(Z\text{.}\) The amount of money a single student will spend on her statistics books is a random variable, and we represent it by \(X\text{.}\)
Random variable.
A random process or variable with a numerical outcome.
The possible outcomes of \(X\) are labeled with a corresponding lower case letter \(x\) and subscripts. For example, we write \(x_1=$0\text{,}\) \(x_2=$137\text{,}\) and \(x_3=$170\text{,}\) which occur with probabilities \(0.20\text{,}\) \(0.55\text{,}\) and \(0.25\text{.}\) The distribution of \(X\) is summarized in Figure 3.5.4 and Table 3.5.11.
| \(i\) | 1 | 2 | 3 | Total |
| \(x_i\) | $0 | $137 | $170 | – |
| \(P(x_i)\) | 0.20 | 0.55 | 0.25 | 1.00 |
We computed the average outcome of \(X\) as $117.85 in Solution 3.5.5.1. We call this average the expected value of \(X\text{,}\) denoted by \(E(X)\text{.}\) The expected value of a random variable is computed by adding each outcome weighted by its probability:
Expected value of a discrete random variable.
If \(X\) takes outcomes \(x_1\text{,}\) \(x_2\text{,}\) ..., \(x_n\) with probabilities \(P(x_1)\text{,}\) \(P(x_2)\text{,}\) ..., \(P(x_n)\text{,}\) the mean, or expected value, of \(X\) is the sum of each outcome multiplied by its corresponding probability:
The expected value for a random variable represents the average outcome. For example, \(E(X)=117.85\) represents the average amount the bookstore expects to make from a single student, which we could also write as \(\mu=117.85\text{.}\) While the bookstore will make more than this on some students and less than this on other students, the average of many randomly selected students will be near $117.85.
It is also possible to compute the expected value of a continuous random variable (see Section 3.6). However, it requires a little calculus and we save it for a later class. 4
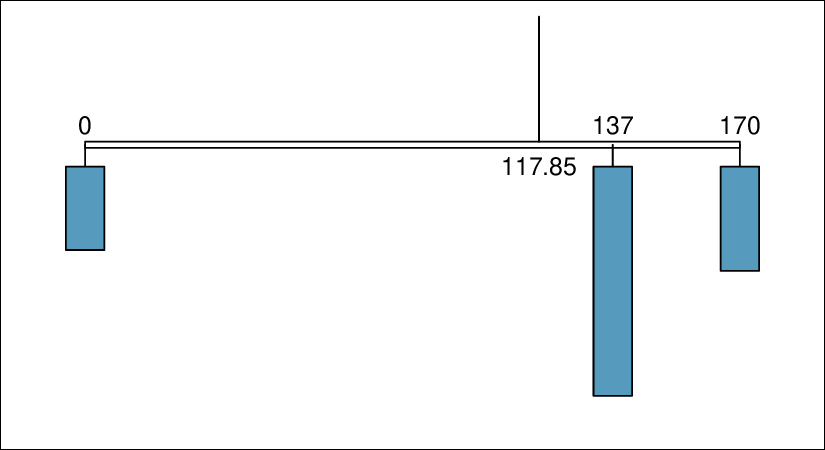
In physics, the expectation holds the same meaning as the center of gravity. The distribution can be represented by a series of weights at each outcome, and the mean represents the balancing point. This is represented in Figure 3.5.4 and Figure 3.5.12. The idea of a center of gravity also expands to continuous probability distributions. Figure 3.5.13 shows a continuous probability distribution balanced atop a wedge placed at the mean.
Subsection 3.5.5 Variability in random variables
Suppose you ran the university bookstore. Besides how much revenue you expect to generate, you might also want to know the volatility (variability) in your revenue.
The variance and standard deviation can be used to describe the variability of a random variable. Subsection 2.2.3 introduced a method for finding the variance and standard deviation for a data set. We first computed deviations from the mean (\(x_i - \mu\)), squared those deviations, and took an average to get the variance. In the case of a random variable, we again compute squared deviations. However, we take their sum weighted by their corresponding probabilities, just like we did for the expectation. This weighted sum of squared deviations equals the variance, and we calculate the standard deviation by taking the square root of the variance, just as we did in Subsection 2.2.3.
Variance and standard deviation of a discrete random variable.
If \(X\) takes outcomes \(x_1\text{,}\) \(x_2\text{,}\) ..., \(x_n\) with probabilities \(P(x_1)\text{,}\) \(P(x_2)\text{,}\) ..., \(P(x_n)\) and expected value \(\mu_{\scriptscriptstyle{X}}=E(X)\text{,}\) then to find the standard deviation of \(X\text{,}\) we first find the variance and then take its square root.
Just as it is possible to compute the mean of a continuous random variable using calculus, we can also use calculus to compute the variance. 5 However, this topic is beyond the scope of the AP exam.
Example 3.5.14.
Compute the expected value, variance, and standard deviation of \(X\text{,}\) the revenue of a single statistics student for the bookstore.
It is useful to construct a table that holds computations for each outcome separately, then add up the results.
| \(i\) | 1 | 2 | 3 | Total |
| \(x_i\) | $0 | $137 | $170 | |
| \(P(x_i)\) | 0.20 | 0.55 | 0.25 | |
| \(x_i \cdot P(x_i)\) | 0 | 75.35 | 42.50 | 117.85 |
Thus, the expected value is \(\mu_{X}=117.85\text{,}\) which we computed earlier. The variance can be constructed using a similar table:
| \(i\) | 1 | 2 | 3 | Total |
| \(x_i\) | $0 | $137 | $170 | |
| \(P(x_i)\) | 0.20 | 0.55 | 0.25 | |
| \(x_i - \mu_{X}\) | -117.85 | 19.15 | 52.15 | |
| \((x_i-\mu_{X})^2\) | 13888.62 | 366.72 | 2719.62 | |
| \((x_i-\mu_{X})^2\cdot P(x_i)\) | 2777.7 | 201.7 | 679.9 | 3659.3 |
The variance of \(X\) is \(\sigma_{X}^2 = 3659.3\text{,}\) which means the standard deviation is \(\sigma_{X} = \sqrt{3659.3} = $60.49\text{.}\)
Checkpoint 3.5.15.
The bookstore also offers a chemistry textbook for $159 and a book supplement for $41. From past experience, they know about 25% of chemistry students just buy the textbook while 60% buy both the textbook and supplement.
What proportion of students don't buy either book? Assume no students buy the supplement without the textbook.
Let \(Y\) represent the revenue from a single student. Write out the probability distribution of \(Y\text{,}\) i.e. a table for each outcome and its associated probability.
Compute the expected revenue from a single chemistry student.
Find the standard deviation to describe the variability associated with the revenue from a single student. 6
(a) \(100% - 25% - 60% = 15%\) of students do not buy any books for the class. Part (b) is represented by the first two lines in the table below. The expectation for part (c) is given as the total on the line \(y_{i}\cdot P(y_{i})\text{.}\) The result of part (d) is the square-root of the variance listed on in the total on the last line: \(\sigma_{Y}= \sqrt{Var(Y)}=\sqrt{4800}=69.28\)
| \(i\) (scenario) | 1 (noBook) |
2 (notebook) |
3 (both) |
Total |
| \(y_{i}\) | 0.00 | 159.00 | 200.00 | |
| \(P(y_{i})\) | 0.15 | 0.25 | 0.60 | |
| \(y_{i} \cdot P(y_{i})\) | 0/00 | 39.75 | 120.00 | \(E(Y)=159.75\) |
| \(y_{i}- \mu_{Y}\) | -159.75 | -0.75 | 40.25 | |
| \((y_{i}-\mu_{Y})^2\) | 25520.06 | 0.56 | 1620.06 | |
| \((y_{i}-\mu_{Y})^2 \cdot P(y_{i})\) | 3828.0 | 0.1 | 972.0 | \(Var(Y) \approx 4800\) |
Subsection 3.5.6 Linear transformations of a random variable
An online store is selling a limited edition t-shirt. The maximum a person is allowed to buy is 3. Let X be a random variable that represents how many of the t-shirts a t-shirt buyer orders. The probability distribution of X is given in the following table.
| \(x_i\) | 1 | 2 | 3 |
| \(P(x_i)\) | 0.6 | 0.3 | 0.1 |
Using the methods of the previous section we can find that the mean \(\mu_{\scriptscriptstyle{X}} = 1.5\) and the standard deviation \(\sigma_{\scriptscriptstyle{X}} = 0.67\text{.}\) Suppose that the cost of each t-shirt is $30 and that there is flat rate $5 shipping fee. The amount of money a t-shirt buyer pays, then, is \(30X + 5\text{,}\) where X is the number of t-shirts ordered. To calculate the mean and standard deviation for the amount of money a t-shirt buyers pays, we could define a new variable \(Y\) as follows:
Checkpoint 3.5.16.
Verify that the distribution of \(Y\) is given by the table below. 7
| \(y_i\) | $35 | $65 | $95 |
| \(P(y_i)\) | 0.6 | 0.3 | 0.1 |
Using this new table, we can compute the mean and standard deviation of the cost for t-shirt orders. However, because Y is a linear transformation of X, we can use the properties from Subsection 2.2.8. Recall that multiplying every X by 30 multiplies both the mean and standard deviation by 30. Adding 5 only adds 5 to the mean, not the standard deviation. Therefore,
Among t-shirt buyers, they spend an average of $45.00, with a standard deviation of $20.10.
Linear transformations of a random variable.
If \(X\) is a random variable, then a linear transformation is given by \(aX + b\text{,}\) where \(a\) and \(b\) are some fixed numbers.
Subsection 3.5.7 Linear combinations of random variables
So far, we have thought of each variable as being a complete story in and of itself. Sometimes it is more appropriate to use a combination of variables. For instance, the amount of time a person spends commuting to work each week can be broken down into several daily commutes. Similarly, the total gain or loss in a stock portfolio is the sum of the gains and losses in its components.
Example 3.5.17.
John travels to work five days a week. We will use \(X_1\) to represent his travel time on Monday, \(X_2\) to represent his travel time on Tuesday, and so on. Write an equation using \(X_1\text{,}\) ..., \(X_5\) that represents his travel time for the week, denoted by \(W\text{.}\)
His total weekly travel time is the sum of the five daily values:
Breaking the weekly travel time \(W\) into pieces provides a framework for understanding each source of randomness and is useful for modeling \(W\text{.}\)
Example 3.5.18.
It takes John an average of 18 minutes each day to commute to work. What would you expect his average commute time to be for the week?
We were told that the average (i.e. expected value) of the commute time is 18 minutes per day: \(E(X_i) = 18\text{.}\) To get the expected time for the sum of the five days, we can add up the expected time for each individual day:
The expectation of the total time is equal to the sum of the expected individual times. More generally, the expectation of a sum of random variables is always the sum of the expectation for each random variable.
Checkpoint 3.5.19.
Elena is selling a TV at a cash auction and also intends to buy a toaster oven in the auction. If \(X\) represents the profit for selling the TV and \(Y\) represents the cost of the toaster oven, write an equation that represents the net change in Elena's cash. 8
Checkpoint 3.5.20.
Based on past auctions, Elena figures she should expect to make about $175 on the TV and pay about $23 for the toaster oven. In total, how much should she expect to make or spend? 9
Checkpoint 3.5.21.
Would you be surprised if John's weekly commute wasn't exactly 90 minutes or if Elena didn't make exactly $152? Explain. 10
Two important concepts concerning combinations of random variables have so far been introduced. First, a final value can sometimes be described as the sum of its parts in an equation. Second, intuition suggests that putting the individual average values into this equation gives the average value we would expect in total. This second point needs clarification — it is guaranteed to be true in what are called linear combinations of random variables.
A linear combination of two random variables \(X\) and \(Y\) is a fancy phrase to describe a combination
where \(a\) and \(b\) are some fixed and known numbers. For John's commute time, there were five random variables — one for each work day — and each random variable could be written as having a fixed coefficient of 1:
For Elena's net gain or loss, the \(X\) random variable had a coefficient of +1 and the \(Y\) random variable had a coefficient of -1.
When considering the average of a linear combination of random variables, it is safe to plug in the mean of each random variable and then compute the final result. For a few examples of nonlinear combinations of random variables — cases where we cannot simply plug in the means — see the footnote. 11
Linear combinations of random variables and the average result.
If \(X\) and \(Y\) are random variables, then a linear combination of the random variables is given by \(aX + bY\text{,}\) where \(a\) and \(b\) are some fixed numbers. To compute the average value of a linear combination of random variables, plug in the average of each individual random variable and compute the result:
Recall that the expected value is the same as the mean, i.e. \(E(X) = \mu_{X}\text{.}\)
Example 3.5.22.
Leonard has invested $6000 in Google Inc. (stock ticker: GOOG) and $2000 in Exxon Mobil Corp. (XOM). If \(X\) represents the change in Google's stock next month and \(Y\) represents the change in Exxon Mobil stock next month, write an equation that describes how much money will be made or lost in Leonard's stocks for the month.
For simplicity, we will suppose \(X\) and \(Y\) are not in percents but are in decimal form (e.g. if Google's stock increases 1%, then \(X=0.01\text{;}\) or if it loses 1%, then \(X=-0.01\)). Then we can write an equation for Leonard's gain as
If we plug in the change in the stock value for \(X\) and \(Y\text{,}\) this equation gives the change in value of Leonard's stock portfolio for the month. A positive value represents a gain, and a negative value represents a loss.
Checkpoint 3.5.23.
Suppose Google and Exxon Mobil stocks have recently been rising 2.1% and 0.4% per month, respectively. Compute the expected change in Leonard's stock portfolio for next month. 12
Checkpoint 3.5.24.
You should have found that Leonard expects a positive gain in Checkpoint 3.5.23. However, would you be surprised if he actually had a loss this month? 13
Subsection 3.5.8 Variability in linear combinations of random variables
Quantifying the average outcome from a linear combination of random variables is helpful, but it is also important to have some sense of the uncertainty associated with the total outcome of that combination of random variables. The expected net gain or loss of Leonard's stock portfolio was considered in Checkpoint 3.5.23. However, there was no quantitative discussion of the volatility of this portfolio. For instance, while the average monthly gain might be about $134 according to the data, that gain is not guaranteed. Figure 3.5.25 shows the monthly changes in a portfolio like Leonard's during the 36 months from 2009 to 2011. The gains and losses vary widely, and quantifying these fluctuations is important when investing in stocks.
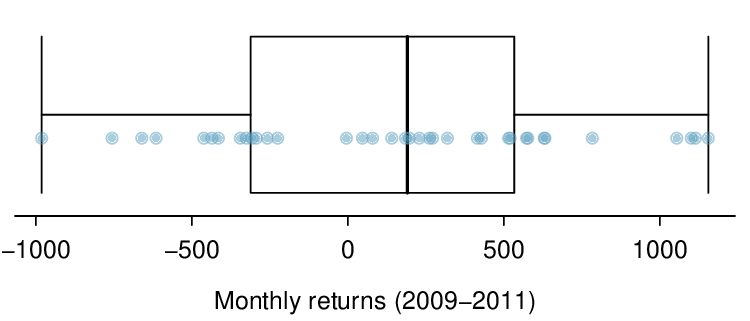
Just as we have done in many previous cases, we use the variance and standard deviation to describe the uncertainty associated with Leonard's monthly returns. To do so, the standard deviations and variances of each stock's monthly return will be useful, and these are shown in Table 3.5.26. The stocks' returns are nearly independent.
| Mean (\(\bar{x}\)) | Standard deviation (\(s\)) | Variance (\(s^2\)) | |
| GOOG | 0.0210 | 0.0849 | 0.0072 |
| XOM | 0.0038 | 0.0520 | 0.0027 |
We want to describe the uncertainty of Leonard's monthly returns by finding the standard deviation of the return on his combined portfolio. First, we note that the variance of a sum has a nice property: the variance of a sum is the sum of the variances. That is, if X and Y are independent random variables:
Because the standard deviation is the square root of the variance, we can rewrite this equation using standard deviations:
This equation might remind you of a theorem from geometry: \(c^2 = a^2 + b^2\text{.}\) The equation for the standard deviation of the sum of two independent random variables looks analogous to the Pythagorean Theorem. Just as the Pythagorean Theorem only holds for right triangles, this equation only holds when X and Y are independent. 14
Standard deviation of the sum and difference of random variables.
If X and Y are independent random variables:
Because \(SD_Y\) = \(SD_{-Y}\text{,}\) the standard deviation of the difference of two variables equals the standard deviation of the sum of two variables. This property holds for more than two variables as well. For example, if X, Y, and Z are independent random variables:
If we need the standard deviation of a linear combination of independent variables, such as \(aX + bY\text{,}\) we can consider \(aX\) and \(bY\) as two new variables. Recall that multiplying all of the values of variable by a positive constant multiplies the standard deviation by that constant. Thus, \(SD_{aX}\) = \(a \times SD_X\) and \(SD_{bY}\) = \(b \times SD_Y\text{.}\) It follows that:
This equation can be used to compute the standard deviation of Leonard's monthly return. Recall that Leonard has $6,000 in Google stock and $2,000 in Exxon Mobil's stock. From Table 3.5.26, the standard deviation of Google stock is 0.0849 and the standard deviation of Exxon Mobile stock is 0.0520.
The standard deviation of the total is $520. While an average monthly return of $134 on an $8000 investment is nothing to scoff at, the monthly returns are so volatile that Leonard should not expect this income to be very stable.
Standard deviation of linear combinations of random variables.
To find the standard deviation of a linear combination of random variables, we first consider \(aX\) and \(bY\) separately. We find the standard deviation of each, and then we apply the equation for the standard deviation of the sum of two variables:
This equation is valid as long as the random variables \(X\) and \(Y\) are independent of each other.
Example 3.5.27.
Suppose John's daily commute has a standard deviation of 4 minutes. What is the uncertainty in his total commute time for the week?
The expression for John's commute time is
Each coefficient is 1, so the standard deviation of the total weekly commute time is
The standard deviation for John's weekly work commute time is about 9 minutes.
Checkpoint 3.5.28.
The computation in Solution 3.5.27.1 relied on an important assumption: the commute time for each day is independent of the time on other days of that week. Do you think this is valid? Explain. 15
Checkpoint 3.5.29.
Consider Elena's two auctions from Checkpoint 3.5.19. Suppose these auctions are approximately independent and the variability in auction prices associated with the TV and toaster oven can be described using standard deviations of $25 and $8. Compute the standard deviation of Elena's net gain. 16
Consider again Checkpoint 3.5.29. The negative coefficient for \(Y\) in the linear combination was eliminated when we squared the coefficients. This generally holds true: negatives in a linear combination will have no impact on the variability computed for a linear combination, but they do impact the expected value computations.
Subsection 3.5.9 Section summary
A discrete probability distribution can be summarized in a table that consists of all possible outcomes of a random variable and the probabilities of those outcomes. The outcomes must be disjoint, and the sum of the probabilities must equal 1.
A probability distribution can be represented with a histogram and, like the distributions of data that we saw in Chapter 2, can be summarized by its center, spread, and shape.
-
When given a probability distribution table, we can calculate the mean (expected value) and standard deviation of a random variable using the following formulas.
\begin{align*} E(X) = \mu_{\scriptscriptstyle{X}} \amp = \sum{x_i\cdot P(x_i)} \amp\\ \amp = x_1\cdot P(x_1) + x_2\cdot P(x_2) + \cdots + x_n\cdot P(x_n)\\ Var(X) = \sigma^2_x \amp = \sum(x_i - \mu_{\scriptscriptstyle{X}})^2 \cdot P(x_i)\\ SD(X) = \sigma_{\scriptscriptstyle{X}} \amp =\sqrt{\sum(x_i - \mu_{\scriptscriptstyle{X}})^2 \cdot P(x_i)}\\ \amp =\sqrt{(x_1-\mu_{\scriptscriptstyle{X}})^2\cdot P(x_1) + (x_2-\mu_{\scriptscriptstyle{X}})^2\cdot P(x_2) + \cdots + (x_n-\mu_{\scriptscriptstyle{X}})^2\cdot P(x_n) } \end{align*}We can think of \(P(x_i)\) as the weight, and each term is weighted its appropriate amount.
The mean of a probability distribution does not need to be a value in the distribution. It represents the average of many, many repetitions of a random process. The standard deviation represents the typical variation of the outcomes from the mean, when the random process is repeated over and over.
Linear transformations. Adding a constant to every value in a probability distribution adds that value to the mean, but it does not affect the standard deviation. When multiplying every value by a constant, this multiplies the mean by the constant and it multiplies the standard deviation by the absolute value of the constant.
-
Combining random variables. Let \(X\) and \(Y\) be random variables and let \(a\) and \(b\) be constants.
The expected value of the sum is the sum of the expected values.
\(E(X+Y) = E(X) + E(Y)\)
\(E(aX+bY) = a\times E(X) + b\times E(Y)\)
When X and Y are independent: The standard deviation of a sum or a difference is the square root of the sum of each standard deviation squared.
\(SD(X + Y) = \sqrt{(SD(X))^2 + (SD(Y))^2}\)
\(SD(X - Y) = \sqrt{(SD(X))^2 + (SD(Y))^2}\)
\(SD(aX + bY) = \sqrt{(a\times SD(X))^2 + (b\times SD(Y))^2}\)
The SD properties require that \(X\) and \(Y\) be independent. The expected value properties hold true whether or not \(X\) and \(Y\) are independent.
Exercises 3.5.10 Exercises
1. College smokers.
At a university, 13% of students smoke.
Calculate the expected number of smokers in a random sample of 100 students from this university.
The university gym opens at 9 am on Saturday mornings. One Saturday morning at 8:55 am there are 27 students outside the gym waiting for it to open. Should you use the same approach from part (a) to calculate the expected number of smokers among these 27 students?
(a) 13.
(b) No, these 27 students are not a random sample from the university's student population. For example, it might be argued that the proportion of smokers among students who go to the gym at 9 am on a Saturday morning would be lower than the proportion of smokers in the university as a whole.
2. Ace of clubs wins.
Consider the following card game with a well-shuffled deck of cards. If you draw a red card, you win nothing. If you get a spade, you win $5. For any club, you win $10 plus an extra $20 for the ace of clubs.
Create a probability model for the amount you win at this game. Also, find the expected winnings for a single game and the standard deviation of the winnings.
What is the maximum amount you would be willing to pay to play this game? Explain your reasoning.
3. Hearts win.
In a new card game, you start with a well-shuffled full deck and draw 3 cards without replacement. If you draw 3 hearts, you win $50. If you draw 3 black cards, you win $25. For any other draws, you win nothing.
Create a probability model for the amount you win at this game, and find the expected winnings. Also compute the standard deviation of this distribution.
If the game costs $5 to play, what would be the expected value and standard deviation of the net profit (or loss)? (Hint: profit = winnings \(-\) cost; \(X-5\))
If the game costs $5 to play, should you play this game? Explain.
(a) \(E(X) = 3.59\text{.}\) \(SD(X) = 9.64\text{.}\)
(b) \(E(X) = -1.41\text{.}\) \(SD(X) = 9.64\text{.}\)
(c) No, the expected net profit is negative, so on average you expect to lose money.
4. Is it worth it?
Andy is always looking for ways to make money fast. Lately, he has been trying to make money by gambling. Here is the game he is considering playing: The game costs $2 to play. He draws a card from a deck. If he gets a number card (2-10), he wins nothing. For any face card ( jack, queen or king), he wins $3. For any ace, he wins $5, and he wins an extra $20 if he draws the ace of clubs.
Create a probability model and find Andy's expected profit per game.
Would you recommend this game to Andy as a good way to make money? Explain.
5. Portfolio return.
A portfolio's value increases by 18% during a financial boom and by 9% during normal times. It decreases by 12% during a recession. What is the expected return on this portfolio if each scenario is equally likely?
5% increase in value.
6. Baggage fees.
An airline charges the following baggage fees: $25 for the first bag and $35 for the second. Suppose 54% of passengers have no checked luggage, 34% have one piece of checked luggage and 12% have two pieces. We suppose a negligible portion of people check more than two bags.
Build a probability model, compute the average revenue per passenger, and compute the corresponding standard deviation.
About how much revenue should the airline expect for a flight of 120 passengers? With what standard deviation? Note any assumptions you make and if you think they are justified.
7. American roulette.
The game of American roulette involves spinning a wheel with 38 slots: 18 red, 18 black, and 2 green. A ball is spun onto the wheel and will eventually land in a slot, where each slot has an equal chance of capturing the ball. Gamblers can place bets on red or black. If the ball lands on their color, they double their money. If it lands on another color, they lose their money. Suppose you bet $1 on red. What's the expected value and standard deviation of your winnings?
\(E = -0.0526\text{.}\) \(SD = 0.9986\text{.}\)
8. European roulette.
The game of European roulette involves spinning a wheel with 37 slots: 18 red, 18 black, and 1 green. A ball is spun onto the wheel and will eventually land in a slot, where each slot has an equal chance of capturing the ball. Gamblers can place bets on red or black. If the ball lands on their color, they double their money. If it lands on another color, they lose their money.
Suppose you play roulette and bet $3 on a single round. What is the expected value and standard deviation of your total winnings?
Suppose you bet $1 in three different rounds. What is the expected value and standard deviation of your total winnings?
How do your answers to parts (a) and (b) compare? What does this say about the riskiness of the two games?
