Section 8.3 Inference for the slope of a regression line
¶Here we encounter our last confidence interval and hypothesis test procedures, this time for making inferences about the slope of the population regression line. We can use this to answer questions such as the following:
Is the unemployment rate a significant linear predictor for the loss of the President's party in the House of Representatives?
On average, how much less in college gift aid do students receive when their parents earn an additional $1000 in income?
Subsection 8.3.1 Learning objectives
Recognize that the slope of the sample regression line is a point estimate and has an associated standard error.
Be able to read the results of computer regression output and identify the quantities needed for inference for the slope of the regression line, specifically the slope of the sample regression line, the \(SE\) of the slope, and the degrees of freedom.
State and verify whether or not the conditions are met for inference on the slope of the regression line based using the \(t\)-distribution.
Carry out a complete confidence interval procedure for the slope of the regression line.
Carry out a complete hypothesis test for the slope of the regression line.
Distinguish between when to use the \(t\)-test for the slope of a regression line and when to use the matched pairs \(t\)-test for a mean of differences.
Subsection 8.3.2 The role of inference for regression parameters
Previously, we found the equation of the regression line for predicting gift aid from family income at Elmhurst College. The slope, \(b\text{,}\) was equal to \(-0.0431\text{.}\) This is the slope for our sample data. However, the sample was taken from a larger population. We would like to use the slope computed from our sample data to estimate the slope of the population regression line.
The equation for the population regression line can be written as
Here, \(\alpha\) and \(\beta\) represent two model parameters, namely the \(y\)-intercept and the slope of the true or population regression line. (This use of \(\alpha\) and \(\beta\) have nothing to do with the \(\alpha\) and \(\beta\) we used previously to represent the probability of a Type I Error and Type II Error!) The parameters \(\alpha\) and \(\beta\) are estimated using data. We can look at the equation of the regression line calculated from a particular data set:
and see that \(a\) and \(b\) are point estimates for \(\alpha\) and \(\beta\text{,}\) respectively. If we plug in the values of \(a\) and \(b\text{,}\) the regression equation for predicting gift aid based on family income is:
The slope of the sample regression line, \(-0.0431\text{,}\) is our best estimate for the slope of the population regression line, but there is variability in this estimate since it is based on a sample. A different sample would produce a somewhat different estimate of the slope. The standard error of the slope tells us the typical variation in the slope of the sample regression line and the typical error in using this slope to estimate the slope of the population regression line.
We would like to construct a 95% confidence interval for \(\beta\text{,}\) the slope of the population regression line. As with means, inference for the slope of a regression line is based on the \(t\)-distribution.
Inference for the slope of a regression line.
Inference for the slope of a regression line is based on the \(t\)-distribution with \(n-2\) degrees of freedom, where \(n\) is the number of paired observations.
Once we verify that conditions for using the \(t\)-distribution are met, we will be able to construct the confidence interval for the slope using a critical value \(t^{\star}\) based on \(n-2\) degrees of freedom. We will use a table of the regression summary to find the point estimate and standard error for the slope.
Subsection 8.3.3 Conditions for the least squares line
Conditions for inference in the context of regression can be more complicated than when dealing with means or proportions.
Inference for parameters of a regression line involves the following assumptions:
Linearity. The true relationship between the two variables follows a linear trend. We check whether this is reasonable by examining whether the data follows a linear trend. If there is a nonlinear trend (e.g. left panel of Figure 8.3.1), an advanced regression method from another book or later course should be applied.
Nearly normal residuals. For each \(x\)-value, the residuals should be nearly normal. When this assumption is found to be unreasonable, it is usually because of outliers or concerns about influential points. An example which suggestions non-normal residuals is shown in the second panel of Figure 8.3.1. If the sample size \(n\ge 30\text{,}\) then this assumption is not necessary.
Constant variability. The variability of points around the true least squares line is constant for all values of \(x\text{.}\) An example of non-constant variability is shown in the third panel of Figure 8.3.1.
Independent. The observations are independent of one other. The observations can be considered independent when they are collected from a random sample or randomized experiment. Be careful of data collected sequentially in what is called a time series. An example of data collected in such a fashion is shown in the fourth panel of Figure 8.3.1.
We see in Figure 8.3.1, that patterns in the residual plots suggest that the assumptions for regression inference are not met in those four examples. In fact, identifying nonlinear trends in the data, outliers, and non-constant variability in the residuals are often easier to detect in a residual plot than in a scatterplot.
We note that the second assumption regarding nearly normal residuals is particularly difficult to assess when the sample size is small. We can make a graph, such as a histogram, of the residuals, but we cannot expect a small data set to be nearly normal. All we can do is to look for excessive skew or outliers. Outliers and influential points in the data can be seen from the residual plot as well as from a histogram of the residuals.
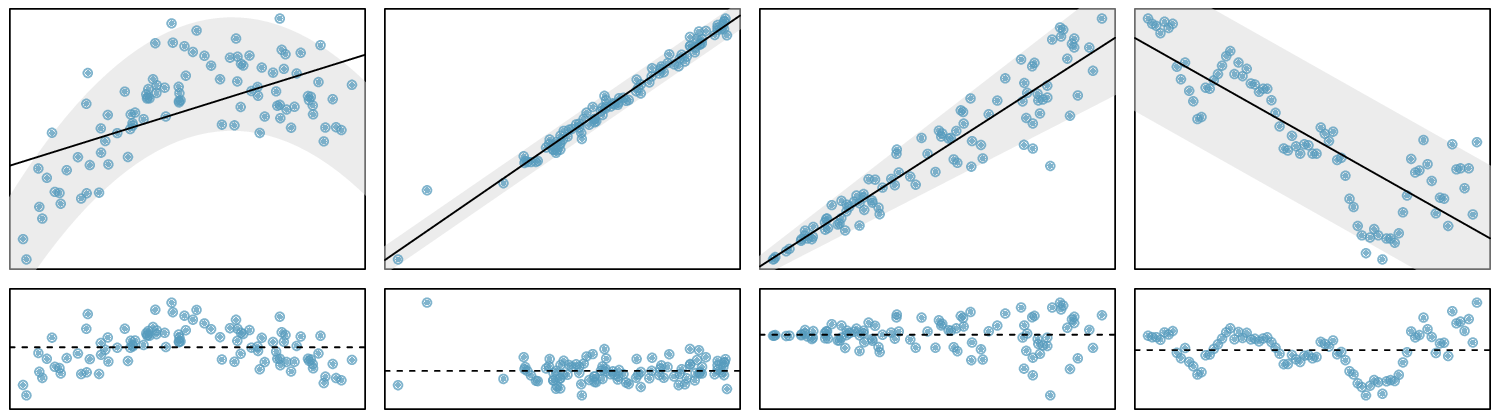
Conditions for inference on the slope of a regression line.
The data is collected from a random sample or randomized experiment.
The residual plot appears as a random cloud of points and does not have any patterns or significant outliers that would suggest that the linearity, nearly normal residuals, constant variability, or independence assumptions are unreasonable.
Subsection 8.3.4 Constructing a confidence interval for the slope of a regression line
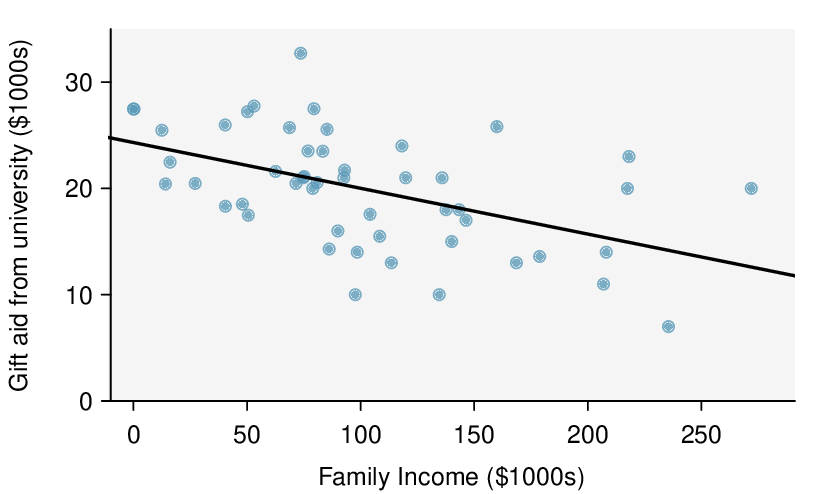
We would like to construct a confidence interval for the slope of the regression line for predicting gift aid based on family income for all freshmen at Elmhurst college.
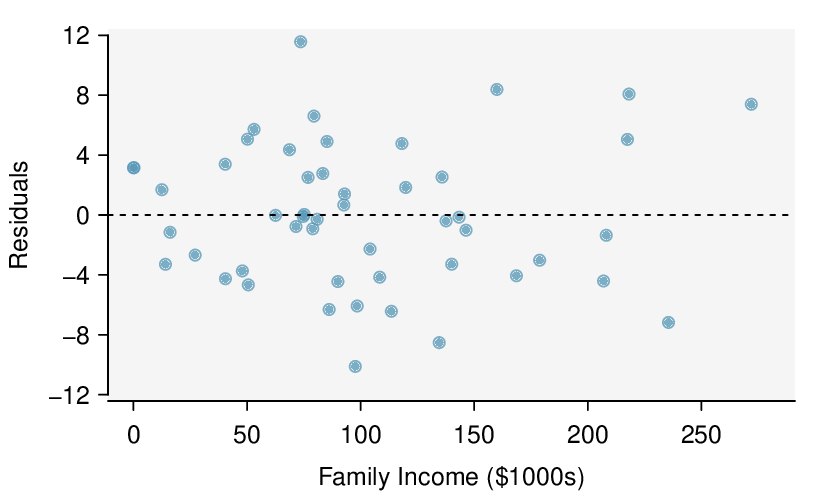
Do conditions seem to be satisfied? We recall that the 50 freshmen in the sample were randomly chosen, so the observations are independent. Next, we need to look carefully at the scatterplot and the residual plot.
Always check conditions.
Do not blindly apply formulas or rely on regression output; always first look at a scatterplot or a residual plot. If conditions for fitting the regression line are not met, the methods presented here should not be applied.
The scatterplot seems to show a linear trend, which matches the fact that there is no curved trend apparent in the residual plot. Also, the standard deviation of the residuals is mostly constant for different \(x\) values and there are no outliers or influential points. There are no patterns in the residual plot that would suggest that a linear model is not appropriate, so the conditions are reasonably met. We are now ready to calculate the 95% confidence interval.
| Estimate | Std. Error | t value | Pr\((>|t|)\) | |
| (Intercept) | 24.3193 | 1.2915 | 18.83 | 0.0000 |
| family_income | -0.0431 | 0.0108 | -3.98 | 0.0002 |
Example 8.3.4.
Construct a 95% confidence interval for the slope of the regression line for predicting gift aid from family income at Elmhurst college.
As usual, the confidence interval will take the form:
The point estimate for the slope of the population regression line is the slope of the sample regression line: \(-0.0431\text{.}\) The standard error of the slope can be read from the table as 0.0108. Note that we do not need to divide 0.0108 by the square root of \(n\) or do any further calculations on 0.0108; 0.0108 is the \(SE\) of the slope. Note that the value of \(t\) given in the table refers to the test statistic, not to the critical value \(t^{\star}\text{.}\) To find \(t^{\star}\) we can use a \(t\)-table. Here \(n=50\text{,}\) so \(df=50-2=48\text{.}\) Using a \(t\)-table, we round down to row \(df=40\) and we estimate the critical value \(t^{\star}=2.021\) for a 95% confidence level. The confidence interval is calculated as:
Note: \(t^{\star}\) using exactly 48 degrees of freedom is equal to 2.01 and gives the same interval of \((-0.065,\ -0.021)\text{.}\)
Example 8.3.5.
Intepret the confidence interval in context. What can we conclude?
We are 95% confident that the slope of the population regression line, the true average change in gift aid for each additional $1000 in family income, is between \(-$0.065\) thousand dollars and \(-$0.021\) thousand dollars. That is, we are 95% confident that, on average, when family income is $1000 higher, gift aid is between $21 and $65 lower.
Because the entire interval is negative, we have evidence that the slope of the population regression line is less than 0. In other words, we have evidence that there is a significant negative linear relationship between gift aid and family income.
Constructing a confidence interval for the slope of regression line.
To carry out a complete confidence interval procedure to estimate the slope of the population regression line \(\beta\text{,}\)
Identify: Identify the parameter and the confidence level, C%.
The parameter will be a slope of the population regression line, e.g. the slope of the population regression line relating air quality index to average rainfall per year for each city in the United States.
Choose: Choose the correct interval procedure and identify it by name.
Here we use choose the \(t\)-interval for the slope.
Check: Check conditions for using a \(t\)-interval for the slope.
Data come from a random sample or randomized experiment.
The residual plot shows no pattern implying that a linear model is reasonable. More specifically, the residuals should be independent, nearly normal (or \(n\ge 30\)), and have constant standard deviation.
Calculate: Calculate the confidence interval and record it in interval form.
-
\(\text{ point estimate } \ \pm\ t^{\star} \times SE\ \text{ of estimate }\text{,}\) \(df = n - 2\)
point estimate: the slope \(b\) of the sample regression line
\(SE\) of estimate: \(SE\) of slope (find using computer output)
\(t^{\star}\text{:}\) use a \(t\)-distribution with \(df = n-2\) and confidence level C
(,)
Conclude: Interpret the interval and, if applicable, draw a conclusion in context.
We are C% confident that the true slope of the regression line, the average change in [y] for each unit increase in [x], is between and . If applicable, draw a conclusion based on whether the interval is entirely above, is entirely below, or contains the value 0.
Example 8.3.7.
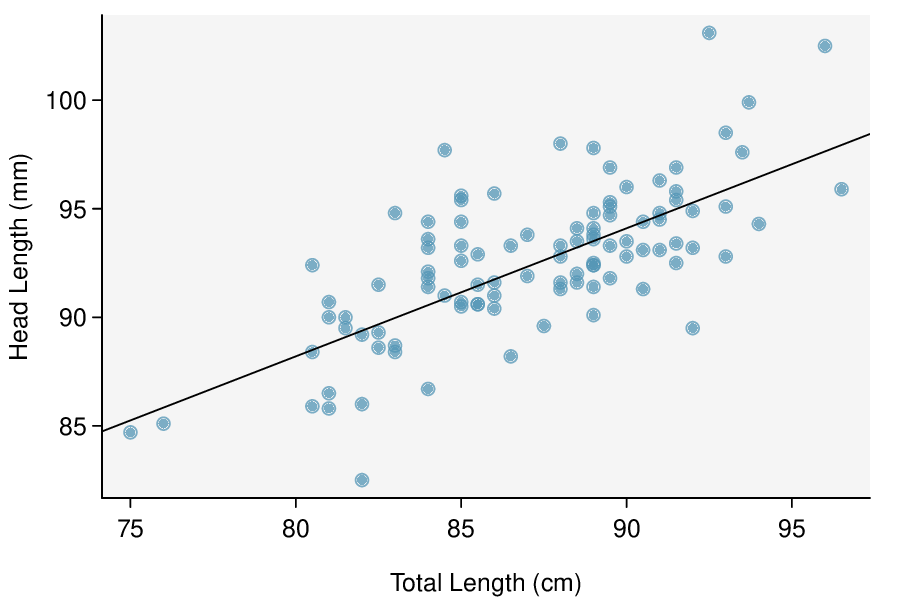
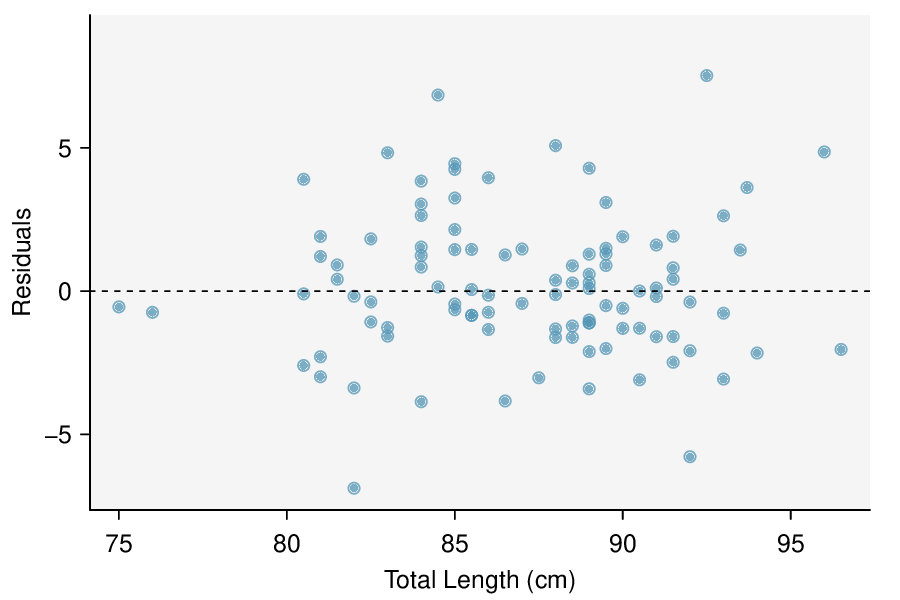
The regression summary below shows statistical software output from fitting the least squares regression line for predicting head length from total length for 104 brushtail possums. The scatterplot and residual plot are shown above.
Predictor Coef SE Coef T P Constant 42.70979 5.17281 8.257 5.66e-13 total_length 0.57290 0.05933 9.657 4.68e-16 S = 2.595 R-Sq = 47.76% R-Sq(adj) = 47.25%
Construct a 95% confidence interval for the slope of the regression line. Is there convincing evidence that there is a positive, linear relationship between head length and total length? Use the five step framework to organize your work.
Identify: The parameter of interest is the slope of the population regression line for predicting head length from body length. We want to estimate this at the 95% confidence level.
Choose: Because the parameter to be estimated is the slope of a regression line, we will use the \(t\)-interval for the slope.
Check: These data come from a random sample. The residual plot shows no pattern. In general, the residuals have constant standard deviation and there are no outliers or influential points. Also \(n=104\ge 30\) so some skew in the residuals would be acceptable. A linear model is reasonable here.
Calculate: We will calculate the interval: \(\text{ point estimate } \ \pm\ t^{\star} \times SE\ \text{ of estimate }\)
We read the slope of the sample regression line and the corresponding \(SE\) from the table. The point estimate is \(b = 0.57290\text{.}\) The \(SE\) of the slope is 0.05933, which can be found next to the slope of 0.57290. The degrees of freedom is \(df=n-2=104-2=102\text{.}\) As before, we find the critical value \(t^{\star}\) using a \(t\)-table (the \(t^{\star}\) value is not the same as the \(T\)-statistic for the hypothesis test). Using the \(t\)-table at row \(df = 100\) (round down since 102 is not on the table) and confidence level 95%, we get \(t^{\star}=1.984\text{.}\)
So the 95% confidence interval is given by:
Conclude: We are 95% confident that the slope of the population regression line is between 0.456 and 0.691. That is, we are 95% confident that the true average increase in head length for each additional cm in total length is between 0.456mm and 0.691mm. Because the interval is entirely above 0, we do have evidence of a positive linear association between the head length and body length for brushtail possums.
Subsection 8.3.5 Calculator: the linear regression \(t\)-interval for the slope
¶We will rely on regression output from statistical software when constructing confidence intervals for the slope of a regression line. We include calculator instructions here simply for completion.
TI-84: T-interval for \(\beta\).
Use STAT, TESTS, LinRegTInt.
Choose
STAT.Right arrow to
TESTS.-
Down arrow and choose
G:LinRegTInt.This test is not built into the TI-83.
Let
XlistbeL1andYlistbeL2. (Don't forget to enter the \(x\) and \(y\) values inL1andL2before doing this interval.)Let
Freqbe1.Enter the desired confidence level.
Leave
RegEQblank.-
Choose
Calculateand hitENTER, which returns:(,) the confidence interval b\(b\text{,}\) the slope of best fit line of the sample data dfdegrees of freedom associated with this confidence interval sstandard deviation of the residuals (not the same as \(SE\) of the slope) a\(a\text{,}\) the y-intercept of the best fit line of the sample data \(r^2\) \(R^2\text{,}\) the explained variance r\(r\text{,}\) the correlation coefficient
Subsection 8.3.6 Midterm elections and unemployment
Elections for members of the United States House of Representatives occur every two years, coinciding every four years with the U.S. Presidential election. The set of House elections occurring during the middle of a Presidential term are called midterm elections. In America's two-party system, one political theory suggests the higher the unemployment rate, the worse the President's party will do in the midterm elections.
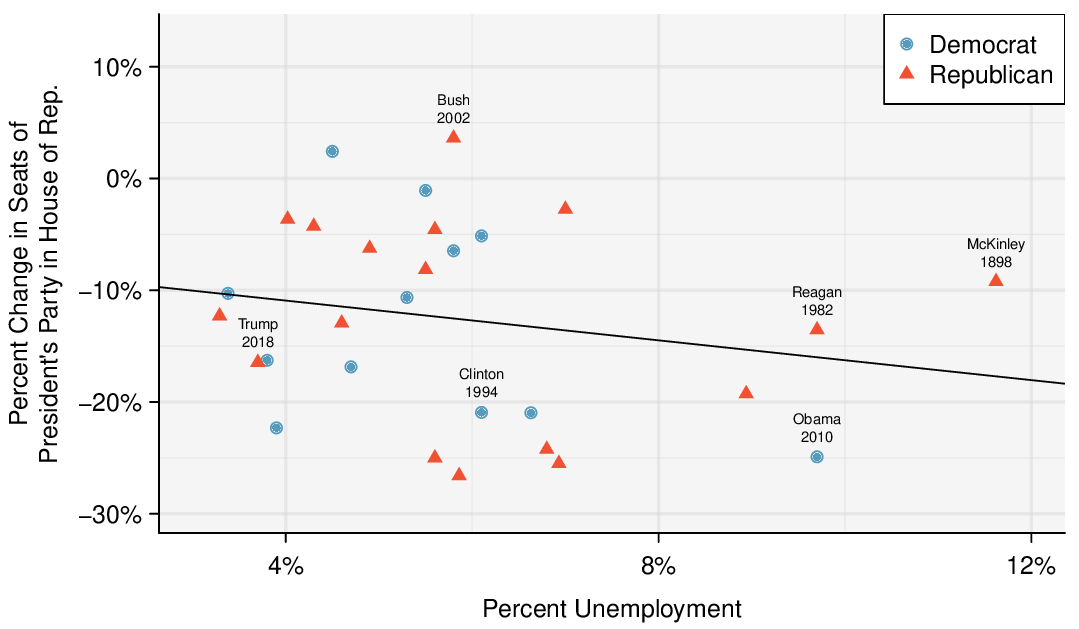
To assess the validity of this claim, we can compile historical data and look for a connection. We consider every midterm election from 1898 to 2018, with the exception of those elections during the Great Depression. Figure 8.3.8 shows these data and the least-squares regression line:
We consider the percent change in the number of seats of the President's party (e.g. percent change in the number of seats for Republicans in 2018) against the unemployment rate.
Examining the data, there are no clear deviations from linearity, the constant variance condition, or the normality of residuals. While the data are collected sequentially, a separate analysis was used to check for any apparent correlation between successive observations; no such correlation was found.
Checkpoint 8.3.9.
The data for the Great Depression (1934 and 1938) were removed because the unemployment rate was 21% and 18%, respectively. Do you agree that they should be removed for this investigation? Why or why not? 1
There is a negative slope in the line shown in Figure 8.3.8. However, this slope (and the y-intercept) are only estimates of the parameter values. We might wonder, is this convincing evidence that the “true” linear model has a negative slope? That is, do the data provide strong evidence that the political theory is accurate? We can frame this investigation as a statistical hypothesis test:
\(\beta = 0\text{.}\) The true linear model has slope zero.
\(\beta \lt 0\text{.}\) The true linear model has a slope less than zero. The higher the unemployment, the greater the loss for the President's party in the House of Representatives.
We would reject \(H_0\) in favor of \(H_A\) if the data provide strong evidence that the slope of the population regression line is less than zero. To assess the hypotheses, we identify a standard error for the estimate, compute an appropriate test statistic, and identify the p-value. Before we calculate these quantities, how good are we at visually determining from a scatterplot when a slope is significantly less than or greater than 0? And why do we tend to use a 0.05 significance level as our cutoff? Try out the following activity which will help answer these questions.
Testing for the slope using a cutoff of 0.05.
What does it mean to say that the slope of the population regression line is significantly greater than 0? And why do we tend to use a cutoff of \(\alpha = 0.05\text{?}\) This 5-minute interactive task will explain: www.openintro.org/why05
Subsection 8.3.7 Understanding regression output from software
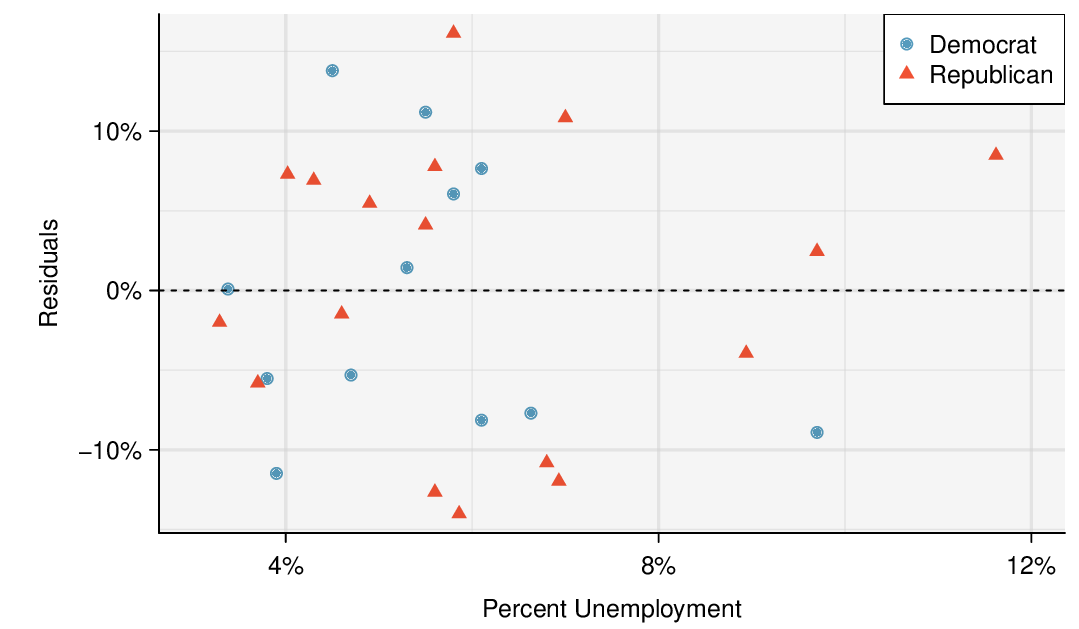
¶The residual plot shown in Figure 8.3.10 shows no pattern that would indicate that a linear model is inappropriate. Therefore we can carry out a test on the population slope using the sample slope as our point estimate. Just as for other point estimates we have seen before, we can compute a standard error and test statistic for \(b\text{.}\) The test statistic \(T\) follows a \(t\)-distribution with \(n-2\) degrees of freedom.
Hypothesis tests on the slope of the regression line.
Use a \(t\)-test with \(n - 2\) degrees of freedom when performing a hypothesis test on the slope of a regression line.
We will rely on statistical software to compute the standard error and leave the explanation of how this standard error is determined to a second or third statistics course. Table 8.3.11 shows software output for the least squares regression line in Figure 8.3.8. The row labeled unemp represents the information for the slope, which is the coefficient of the unemployment variable.
| Estimate | Std. Error | t value | Pr\((>|t|)\) | |
| (Intercept) | -7.3644 | 5.1553 | -1.43 | 0.1646 |
| unemp | -0.8897 | 0.8350 | -1.07 | 0.2961 |
Example 8.3.12.
What do the first column of numbers in the regression summary represent?
The entries in the first column represent the least squares estimates for the \(y\)-intercept and slope, \(a\) and \(b\) respectively. Using this information, we could write the equation for the least squares regression line as
where \(y\) in this case represents the percent change in the number of seats for the president's party, and \(x\) represents the unemployment rate.
We previously used a test statistic \(T\) for hypothesis testing in the context of means. Regression is very similar. Here, the point estimate is \(b=-0.8897\text{.}\) The \(SE\) of the estimate is 0.8350, which is given in the second column, next to the estimate of \(b\text{.}\) This \(SE\) represents the typical error when using the slope of the sample regression line to estimate the slope of the population regression line.
The null value for the slope is 0, so we now have everything we need to compute the test statistic. We have:
This value corresponds to the \(T\)-score reported in the regression output in the third column along the unemp row.
Example 8.3.14.
In this example, the sample size \(n=27\text{.}\) Identify the degrees of freedom and p-value for the hypothesis test.
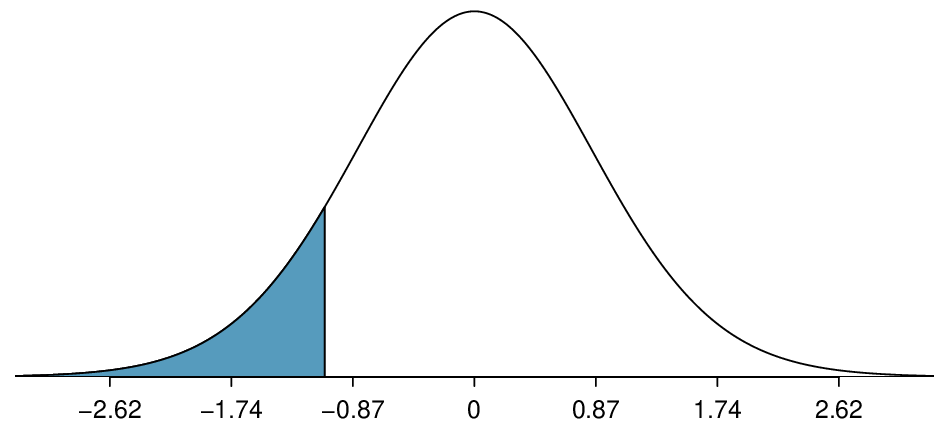
The degrees of freedom for this test is \(n-2\text{,}\) or \(df = 27-2 = 25\text{.}\) We could use a table or a calculator to find the probability of a value less than -1.07 under the \(t\)-distribution with 25 degrees of freedom. However, the two-side p-value is given in Table 8.3.11, next to the corresponding \(t\)-statistic. Because we have a one-sided alternate hypothesis, we take half of this. The p-value for the test is \(\frac{0.2961}{2}=0.148\text{.}\)
Because the p-value is so large, we do not reject the null hypothesis. That is, the data do not provide convincing evidence that a higher unemployment rate is associated with a larger loss for the President's party in the House of Representatives in midterm elections.
Don't carelessly use the p-value from regression output.
The last column in regression output often lists p-values for one particular hypothesis: a two-sided test where the null value is zero. If your test is one-sided and the point estimate is in the direction of \(H_A\text{,}\) then you can halve the software's p-value to get the one-tail area. If neither of these scenarios match your hypothesis test, be cautious about using the software output to obtain the p-value.
Hypothesis test for the slope of regression line.
To carry out a complete hypothesis test for the claim that there is no linear relationship between two numerical variables, i.e. that \(\beta=0\text{,}\)
Identify: Identify the hypotheses and the significance level, \(\alpha\text{.}\)
\(H_0\text{:}\) \(\beta = 0\)
\(H_A\text{:}\) \(\beta \ne 0\text{;}\) \(H_A\text{:}\) \(\beta > 0\text{;}\) or \(H_A\text{:}\) \(\beta \lt 0\)
Choose: Choose the correct test procedure and identify it by name.
Here we choose the \(t\)-test for the slope.
Check: Check conditions for using a \(t\)-test for the slope.
Data come from a random sample or randomized experiment.
The residual plot shows no pattern implying that a linear model is reasonable. More specifically, the residuals should be independent, nearly normal (or \(n\ge 30\)),and have constant standard deviation.
Calculate: Calculate the \(t\)-statistic, \(df\text{,}\) and p-value.
-
\(T= \frac{\text{ point estimate } - \text{ null value } }{SE \text{ of estimate } }\text{,}\) \(df=n-2\)
point estimate: the slope \(b\) of the sample regression line
\(SE\) of estimate: \(SE\) of slope (find using computer output)
null value: 0
p-value = (based on the \(t\)-statistic, the \(df\text{,}\) and the direction of \(H_A\))
Conclude: Compare the p-value to \(\alpha\text{,}\) and draw a conclusion in context.
If the p-value is \(\lt \alpha\text{,}\) reject \(H_0\text{;}\) there is sufficient evidence that [\(H_A\) in context].
If the p-value is \(> \alpha\text{,}\) do not reject \(H_0\text{;}\) there is not sufficient evidence that [\(H_A\) in context].
Example 8.3.15.
The regression summary below shows statistical software output from fitting the least squares regression line for predicting gift aid based on family income for 50 freshman students at Elmhurst College. The scatterplot and residual plot were shown in Figure 8.3.2.
Predictor Coef SE Coef T P Constant 24.31933 1.29145 18.831 < 2e-16 family_income -0.04307 0.01081 -3.985 0.000229 S = 4.783 R-Sq = 24.86% R-Sq(adj) = 23.29%
Do these data provide convincing evidence that there is a negative, linear relationship between family income and gift aid? Carry out a complete hypothesis test at the 0.05 significance level. Use the five step framework to organize your work.
Identify: We will test the following hypotheses at the \(\alpha=0.05\) significance level.
\(H_0\text{:}\) \(\beta = 0\text{.}\) There is no linear relationship.
\(H_A\text{:}\) \(\beta \lt 0\text{.}\) There is a negative linear relationship.
Here, \(\beta\) is the slope of the population regression line for predicting gift aid from family income at Elmhurst College.
Choose: Because the hypotheses are about the slope of a regression line, we choose the \(t\)-test for a slope.
Check: The data come from a random sample. Also, the residual plot shows that the residuals have constant variance and no outliers or influential points (and \(n=50\ge 30\)). The lack of any pattern in the residual plot indicates that a linear model is appropriate.
Calculate: We will calculate the \(t\)-statistic, degrees of freedom, and the p-value.
We read the slope of the sample regression line and the corresponding \(SE\) from the table.
The point estimate is: \(b = -0.04307\text{.}\)
The \(SE\) of the slope is: \(SE = 0.01081\text{.}\)
Because \(H_A\) uses a less than sign (\(\lt\)), meaning that it is a lower-tail test, the p-value is the area to the left of \(t=-3.985\) under the \(t\)-distribution with \(50-2=48\) degrees of freedom. The p-value = \(\frac{1}{2}(0.000229)\approx 0.0001\text{.}\)
Conclude: The p-value of 0.0001 is \(\lt 0.05\text{,}\) so we reject \(H_0\text{;}\) there is sufficient evidence that there is a negative linear relationship between family income and gift aid at Elmhurst College.
Subsection 8.3.8 Calculator: the \(t\)-test for the slope
¶When performing this type of inference, we generally make use of regression output that provides us with the necessary quantities: \(b\) and \(SE \text{ of } {b}\text{.}\) The calculator functions below require knowing all of the data and are, therefore, rarely used. We describe them here for the sake of completion.
TI-83/84: Linear regression T-test on \(\beta\).
Use STAT, TESTS, LinRegTTest.
Choose
STAT.Right arrow to
TESTS.Down arrow and choose
F:LinRegTTest. (On TI-83 it isE:LinRegTTest).Let
XlistbeL1andYlistbeL2. (Don't forget to enter the \(x\) and \(y\) values inL1andL2before doing this test.)Let
Freqbe1.Choose \(\ne\text{,}\) \(\lt\text{,}\) or \(>\) to correspond to \(H_A\text{.}\)
Leave
RegEQblank.-
Choose
Calculateand hitENTER, which returns:tt statistic b\(b\text{,}\) slope of the line pp-value sst. dev. of the residuals dfdegrees of freedom for the test \(r^2\) \(R^2\text{,}\) explained variance a\(a\text{,}\) y-intercept of the line r\(r\text{,}\) correlation coefficient
Casio fx-9750GII: Linear regression T-test on \(\beta\).
Navigate to
STAT(MENUbutton, then hit the2button or selectSTAT).Enter your data into 2 lists.
Select
TEST(F3),t(F2), andREG(F3).If needed, update the sidedness of the test and the
XListandYListlists. TheFreqshould be set to1.-
Hit
EXE, which returns:tt statistic b\(b\text{,}\) slope of the line pp-value sst. dev. of the residuals dfdegrees of freedom for the test r\(r\text{,}\) correlation coefficient a\(a\text{,}\) y-intercept of the line \(r^2\) \(R^2\text{,}\) explained variance
Example 8.3.16.
Why does the calculator test include the symbol \(\rho\) when choosing the direction of the alternate hypothesis?
Recall the we used the letter \(r\) to represent correlation. The Greek letter \(\rho=0\) represents the correlation for the entire population. The slope \(b=r\frac{s_y}{s_x}\text{.}\) If the slope of the population regression line is zero, the correlation for the population must also be zero. For this reason, the \(t\)-test for \(\beta=0\) is equivalent to a test for \(\rho=0\text{.}\)
Subsection 8.3.9 Which inference procedure to use for paired data?
In Subsection 7.2.5, we looked at a set of paired data involving the price of textbooks for UCLA courses at the UCLA Bookstore and on Amazon. The left panel of Figure 8.3.17 shows the difference in price (UCLA Bookstore \(-\) Amazon) for each book. Because we have two data points on each textbook, it also makes sense to construct a scatterplot, as seen in the right panel of Figure 8.3.17.
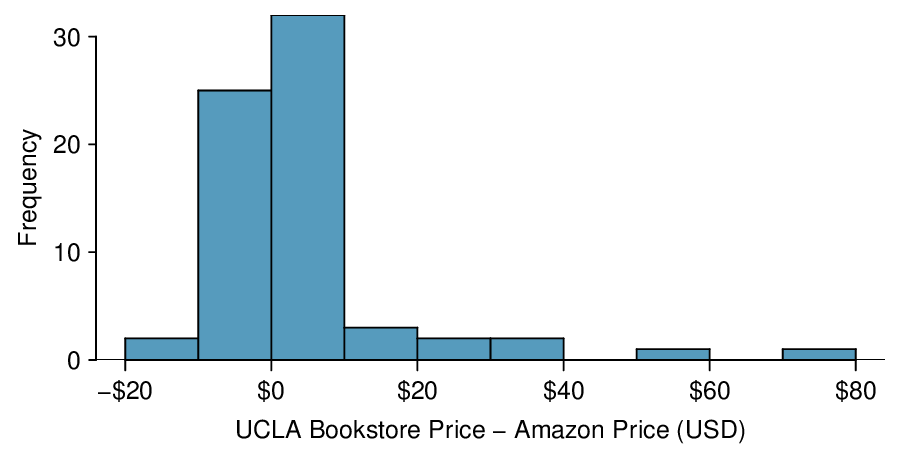
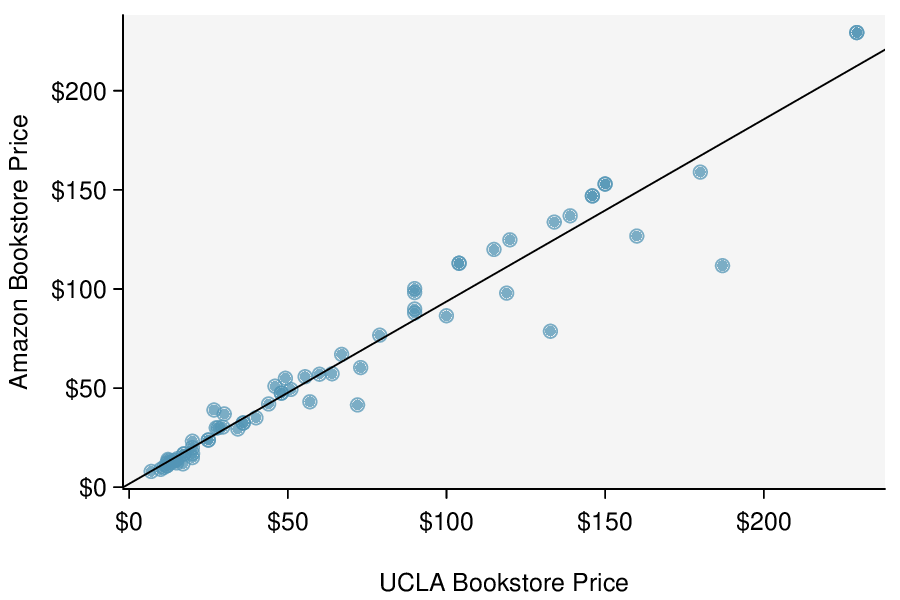
Example 8.3.18.
What additional information does the scatterplot provide about the price of textbooks at UCLA Bookstore and on Amazon?
With a scatterplot, we see the relationship between the variables. We can see when UCLA Bookstore price is larger, whether Amazon price tends to be larger. We can consider the strength of the correlation and we can plot the linear regression equation.
Example 8.3.19.
Which test should we do if we want to check whether:
prices for textbooks for UCLA courses are higher at the UCLA Bookstore than on Amazon
there is a significant, positive linear relationship between UCLA Bookstore price and Amazon price?
In the first case, we are interested in whether the differences (UCLA Bookstore \(-\) Amazon) are, on average, greater than 0, so we would do a matched pairs \(t\)-test for a mean of differences. In the second case, we are interested in whether the slope is significantly greater than 0, so we would do a \(t\)-test for the slope of a regression line.
Likewise, a matched pairs \(t\)-interval for a mean of differences would provide an interval of reasonable values for mean of the differences for all UCLA textbooks, whereas a \(t\)-interval for the slope would provide an interval of reasonable values for the slope of the regression line for all UCLA textbooks.
Inference for paired data.
A matched pairs \(t\)-interval or \(t\)-test for a mean of differences only makes sense when we are asking whether, on average, one variable is greater than another (think histogram of the differences). A \(t\)-interval or \(t\)-test for the slope of a regression line makes sense when we are interested in the linear relationship between them (think scatterplot).
Example 8.3.20.
Previously, we looked at the relationship betweeen body length and head length for bushtail possums. We also looked at the relationship between gift aid and family income for freshmen at Elmhurst College. Could we do a matched pairs \(t\)-test in either of these scenarios?
We have to ask ourselves, does it make sense to ask whether, on average, body length is greater than head length? Similarly, does it make sense to ask whether, on average, gift aid is greater than family income? These don't seem to be meaningful research questions; a matched pairs \(t\)-test for a mean of differences would not be useful here.
Checkpoint 8.3.21.
A teacher gives her class a pretest and a posttest. Does this result in paired data? If so, which hypothesis test should she use? 2
Subsection 8.3.10 Section summary
In Chapter 6, we used a \(\chi^2\) test of independence to test for association between two categorical variables. In this section, we test for association/correlation between two numerical variables.
We use the slope \(b\) as a point estimate for the slope \(\beta\) of the population regression line. The slope of the population regression line is the true increase/decrease in \(y\) for each unit increase in \(x\text{.}\) If the slope of the population regression line is 0, there is no linear relationship between the two variables.
Under certain assumptions, the sampling distribution of \(b\) is normal and the distribution of the standardized test statistic using the standard error of the slope follows a \(t\)-distribution with \(n-2\) degrees of freedom.
-
When there is \((x, y)\) data and the parameter of interest is the slope of the population regression line, e.g. the slope of the population regression line relating air quality index to average rainfall per year for each city in the United States:
Estimate \(\beta\) at the C% confidence level using a \(t\)-interval for the slope.
Test \(H_0\text{:}\) \(\beta=0\) at the \(\alpha\) significance level using a \(t\)-test for the slope.
-
The conditions for the \(t\)-interval and \(t\)-test for the slope of a regression line are the same.
Data come from a random sample or randomized experiment.
The residual plot shows no pattern implying that a linear model is reasonable. More specifically, the residuals should be independent, nearly normal (or \(n\ge 30\)), and have constant standard deviation.
-
The confidence interval and test statistic are calculated as follows:
Confidence interval: \(\text{ point estimate } \ \pm\ t^{\star} \times SE\ \text{ of estimate }\text{,}\) or
-
Test statistic: \(T = \frac{\text{ point estimate } - \text{ null value } }{SE\ \text{ of estimate } }\) and p-value
point estimate: the slope \(b\) of the sample regression line
\(SE\) of estimate: \(SE\) of slope (find using computer output)
\(df = n-2\)
If the confidence interval for the slope of the population regression line estimates the true average increase in the \(y\)-variable for each unit increase in the \(x\)-variable.
The \(t\)-test for the slope and the matched pairs \(t\)-test for a mean of differences both involve paired, numerical data. However, the \(t\)-test for the slope asks if the two variables have a linear relationship, specifically if the slope of the population regression line is different from 0. The matched pairs \(t\)-test for a mean of differences, on the other hand, asks if the two variables are in some way the same, specifically if the mean of the population differences is 0.
Exercises 8.3.11 Exercises
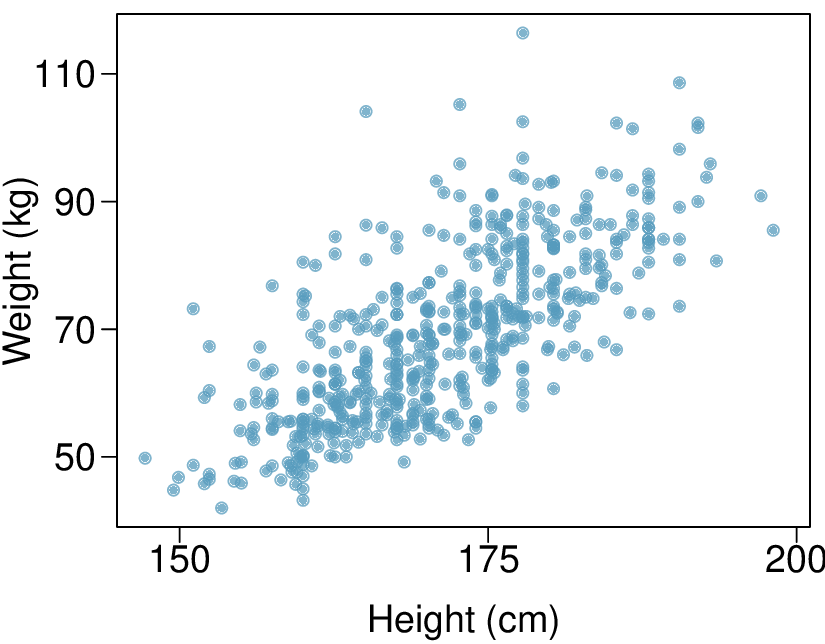
1. Body measurements, Part IV.
The scatterplot and least squares summary below show the relationship between weight measured in kilograms and height measured in centimeters of 507 physically active individuals.
| Estimate | Std. Error | t value | Pr\((>|t|)\) | |
| (Intercept) | -105.0113 | 7.5394 | -13.93 | 0.0000 |
| height | 1.0176 | 0.0440 | 23.13 | 0.0000 |
Describe the relationship between height and weight.
Write the equation of the regression line. Interpret the slope and intercept in context.
Do the data provide strong evidence that an increase in height is associated with an increase in weight? State the null and alternative hypotheses, report the p-value, and state your conclusion.
The correlation coefficient for height and weight is 0.72. Calculate \(R^2\) and interpret it in context.
(a) The relationship is positive, moderate-to-strong, and linear. There are a few outliers but no points that appear to be influential.
(b) \(\widehat{\text{weight} = -105.0113 + 1.0176 \times \text{height}\text{.}\) Slope: For each additional centimeter in height, the model predicts the average weight to be 1.0176 additional kilograms (about 2.2 pounds). Intercept: People who are 0 centimeters tall are expected to weigh -105.0113 kilograms. This is obviously not possible. Here, the \(y\)- intercept serves only to adjust the height of the line and is meaningless by itself.
(c) \(H_{0}:\) The true slope coefficient of height is zero \((\beta_{1} = 0)\text{.}\) \(H_{A}:\) The true slope coefficient of height is different than zero \((\beta_{1} \ne 0)\text{.}\) The p-value for the two-sided alternative hypothesis \((\beta_{1} \ne 0)\) is incredibly small, so we reject \(H_{0}\text{.}\) The data provide convincing evidence that height and weight are positively correlated. The true slope parameter is indeed greater than 0.
(d) \(R^2 = 0.72^2 = 0.52\text{.}\) Approximately 52% of the variability in weight can be explained by the height of individuals.
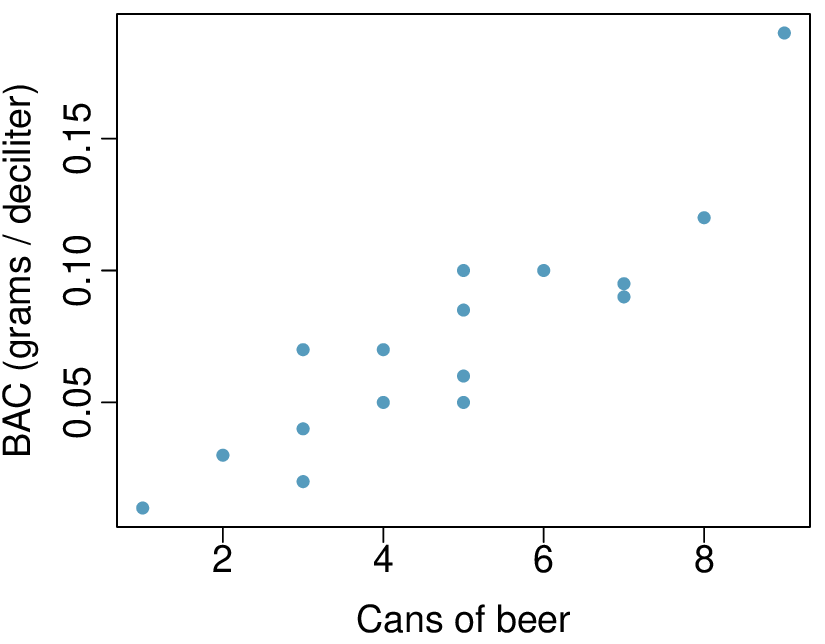
2. Beer and blood alcohol content.
Many people believe that gender, weight, drinking habits, and many other factors are much more important in predicting blood alcohol content (BAC) than simply considering the number of drinks a person consumed. Here we examine data from sixteen student volunteers at Ohio State University who each drank a randomly assigned number of cans of beer. These students were different genders, and they differed in weight and drinking habits. Thirty minutes later, a police officer measured their blood alcohol content (BAC) in grams of alcohol per deciliter of blood. 3 The scatterplot and regression table summarize the findings.
| Estimate | Std. Error | t value | Pr\((>|t|)\) | |
| (Intercept) | -0.0127 | 0.0126 | -1.00 | 0.3320 |
| beers | 0.0180 | 0.0024 | 7.48 | 0.0000 |
Describe the relationship between the number of cans of beer and BAC.
Write the equation of the regression line. Interpret the slope and intercept in context.
Do the data provide strong evidence that drinking more cans of beer is associated with an increase in blood alcohol? State the null and alternative hypotheses, report the p-value, and state your conclusion.
The correlation coefficient for number of cans of beer and BAC is 0.89. Calculate \(R^2\) and interpret it in context.
Suppose we visit a bar, ask people how many drinks they have had, and also take their BAC. Do you think the relationship between number of drinks and BAC would be as strong as the relationship found in the Ohio State study?
3. Spouses, Part II.
The scatterplot below summarizes womens' heights and their spouses' heights for a random sample of 170 married women in Britain, where both partners' ages are below 65 years. Summary output of the least squares fit for predicting spouse's height from the woman's height is also provided in the table.
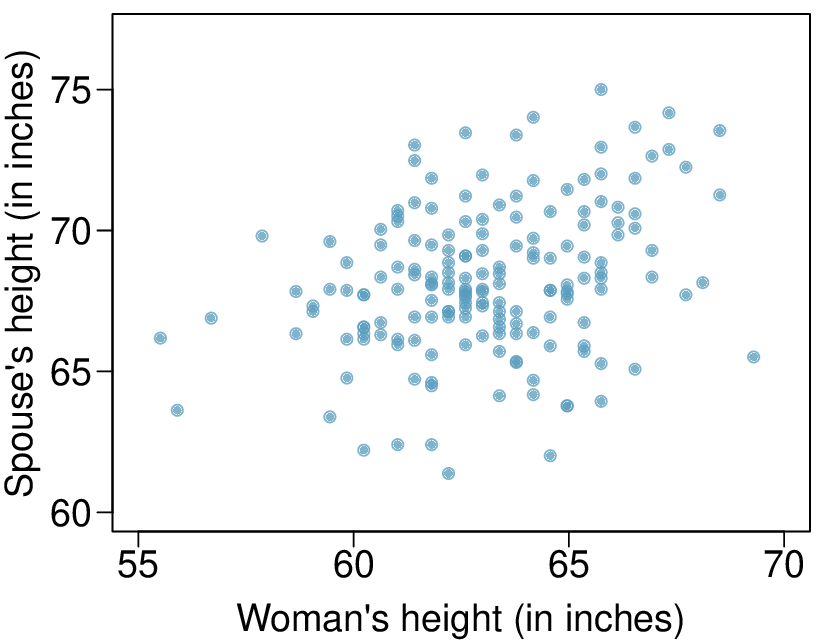
| Estimate | Std. Error | t value | Pr\((>|t|)\) | |
| (Intercept) | 43.5755 | 4.6842 | 9.30 | 0.0000 |
| height_spouse | 0.2863 | 0.0686 | 4.17 | 0.0000 |
Is there strong evidence in this sample that taller women have taller spouses? State the hypotheses and include any information used to conduct the test.
Write the equation of the regression line for predicting the height of a woman's spouse based on the woman's height.
Interpret the slope and intercept in the context of the application.
Given that \(R^2 = 0.09\text{,}\) what is the correlation of heights in this data set?
You meet a married woman from Britain who is 5'9" (69 inches). What would you predict her spouse's height to be? How reliable is this prediction?
You meet another married woman from Britain who is 6'7" (79 inches). Would it be wise to use the same linear model to predict her spouse's height? Why or why not?
(a) \(H_{0}: \beta_{1} = 0\text{;}\) \(H_{A}: \beta_{1} \ne 0\text{.}\) The p-value, as reported in the table, is incredibly small and is smaller than 0.05, so we reject \(H_{0}\text{.}\) The data provide convincing evidence that womens' and spouses' heights are positively correlated.
(b) \(\widehat{\text{height}}_{S} = 43.5755 + 0.2863 \times \text{height}_W\text{.}\)
(c) Slope: For each additional inch in woman's height, the spouse's height is expected to be an additional 0.2863 inches, on average. Intercept: Women who are 0 inches tall are predicted to have spouses who are 43.5755 inches tall. The intercept here is meaningless, and it serves only to adjust the height of the line.
(d) The slope is positive, so \(r\) must also be positive. \(r= \sqrt{0.09} = 0.30\)
(e) 63.2612. Since \(R^2\) is low, the prediction based on this regression model is not very reliable.
(f) No, we should avoid extrapolating.
4. Urban homeowners, Part II.
Exercise 8.2.11.13 gives a scatterplot displaying the relationship between the percent of families that own their home and the percent of the population living in urban areas. Below is a similar scatterplot, excluding District of Columbia, as well as the residuals plot. There were 51 cases.
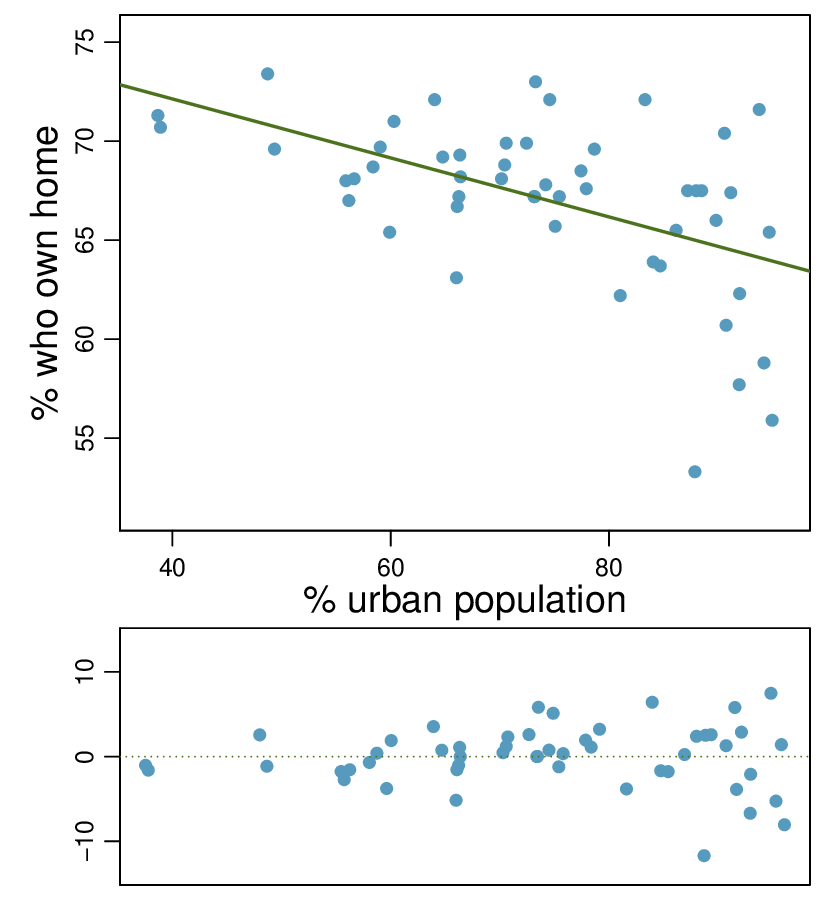
For these data, \(R^2 = 0.28\text{.}\) What is the correlation? How can you tell if it is positive or negative?
Examine the residual plot. What do you observe? Is a simple least squares fit appropriate for these data?
5. Murders and poverty, Part II.
Exercise 8.2.11.9 presents regression output from a model for predicting annual murders per million from percentage living in poverty based on a random sample of 20 metropolitan areas. The model output is also provided below.
| Estimate | Std. Error | t value | Pr\((>|t|)\) | |
| (Intercept) | -29.901 | 7.789 | -3.839 | 0.001 |
| poverty% | 2.559 | 0.390 | 6.562 | 0.000 |
| \(s = 5.512\) | \(R^2 = 70.52\)% | \(R^2_{adj} = 68.89\)% |
What are the hypotheses for evaluating whether poverty percentage is a significant predictor of murder rate?
State the conclusion of the hypothesis test from part (a) in context of the data.
Calculate a 95% confidence interval for the slope of poverty percentage, and interpret it in context of the data.
Do your results from the hypothesis test and the confidence interval agree? Explain.
(a) \(H_{0}: \beta_{1} = 0\text{;}\) \(H_{A}: \beta_{1} \ne 0\)
(b) The p-value for this test is approximately 0, therefore we reject \(H_{0}\text{.}\) The data provide convincing evidence that poverty percentage is a significant predictor of murder rate.
(c) \(n = 20\text{;}\) \(df = 18\text{;}\) \(T^{*}_{18} = 2.10\text{;}\) \(2.559 \pm 2.10 \times 0.390 = (1.74, 3.378)\text{;}\) For each percentage point poverty is higher, murder rate is expected to be higher on average by 1.74 to 3.378 per million.
(d) Yes, we rejected \(H_{0}\) and the confidence interval does not include 0.
6. Babies.
Is the gestational age (time between conception and birth) of a low birth-weight baby useful in predicting head circumference at birth? Twenty-five low birth-weight babies were studied at a Harvard teaching hospital; the investigators calculated the regression of head circumference (measured in centimeters) against gestational age (measured in weeks). The estimated regression line is
What is the predicted head circumference for a baby whose gestational age is 28 weeks?
The standard error for the coefficient of gestational age is 0.35, which is associated with \(df=23\text{.}\) Does the model provide strong evidence that gestational age is significantly associated with head circumference?
