Section 7.1 Inference for a mean with the \(t\)-distribution
¶In this section, we turn our attention to numerical variables and answer questions such as the following:
How well can we estimate the mean income of people in a certain city, county, or state?
What is the average mercury content in various types of fish?
Are people's run times getting faster or slower, on average?
How does the sample size affect the expected error in our estimates?
When is it reasonable to model the sample mean \(\bar{x}\) using a normal distribution, and when will we need to use a new distribution, known as the \(t\)-distribution?
Subsection 7.1.1 Learning objectives
Understand the relationship between a \(t\)-distribution and a normal distribution, and explain why we use a \(t\)-distribution for inference on a mean.
State and verify whether or not the conditions for inference for a mean based on the \(t\)-distribution are met. Understand when it is necessary to look at the distribution of the sample data.
Know the degrees of freedom associated with a one sample \(t\)-procedure.
Carry out a complete hypothesis test for a single mean.
Carry out a complete confidence interval procedure for a single mean.
Find the minimum sample size needed to estimate a mean with C% confidence and a margin of error no greater than a certain value.
Subsection 7.1.2 Using a normal distribution for inference when \(\sigma\) is known
¶In Section 4.2 we saw that the distribution of a sample mean is normal if the population is normal or if the sample size is at least 30. In these problems, we used the population mean and population standard deviation to find a Z-score. However, in the case of inference, these values will be unknown. In rare circumstances we may know the standard deviation of a population, even though we do not know its mean. For example, in some industrial processes, the mean may be known to shift over time, while the standard deviation of the process remains the same. In these cases, we can use the normal model as the basis for our inference procedures. We use \(\bar{x}\) as our point estimate for \(\mu\) and the \(SD\) formula for a sample mean calculated in Section 4.2: \(\sigma_{\bar{x}} =\frac{\sigma}{\sqrt{n}}\text{.}\) That leads to a confidence interval and a test statistic as follows:
What happens if we do not know the population standard deviation \(\sigma\text{,}\) as is usually the case? The best we can do is use the sample standard deviation, denoted by \(s\text{,}\) to estimate the population standard deviation.
However, when we do this we run into a problem: when carrying out our inference procedures, we will be trying to estimate two quantities: both the mean and the standard deviation. Looking at the \(SD\) and \(SE\) formulas, we can make some important observations that will give us a hint as to what will happen when we use \(s\) instead of \(\sigma\text{.}\)
For a given population, \(\sigma\) is a fixed number and does not vary.
\(s\text{,}\) the standard deviation of a sample, will vary from one sample to the next and will not be exactly equal to \(\sigma\text{.}\)
The larger the sample size \(n\text{,}\) the better the estimate \(s\) will tend to be for \(\sigma\text{.}\)
For this reason, the normal model still works well when the sample size is large. For smaller sample sizes, we run into a problem: our use of \(s\text{,}\) which is used when computing the standard error, tends to add more variability to our test statistic. It is this extra variability that leads us to a new distribution: the \(t\)-distribution.
Subsection 7.1.3 Introducing the \(t\)-distribution
¶When we use the sample standard deviation \(s\) in place of the population standard deviation \(\sigma\) to standardize the sample mean, we get an entirely new distribution - one that is similar to the normal distribution, but has greater spread. This distribution is known as the \(t\)-distribution. A \(t\)-distribution, shown as a solid line in Figure 7.1.1, has a bell shape. However, its tails are thicker than the normal model's. We can see that a greater proportion of the area under the \(t\)-distribution is beyond 2 standard units from 0 than under the normal distribution. These extra thick tails are exactly the correction we need to resolve the problem of a poorly estimated standard deviation.

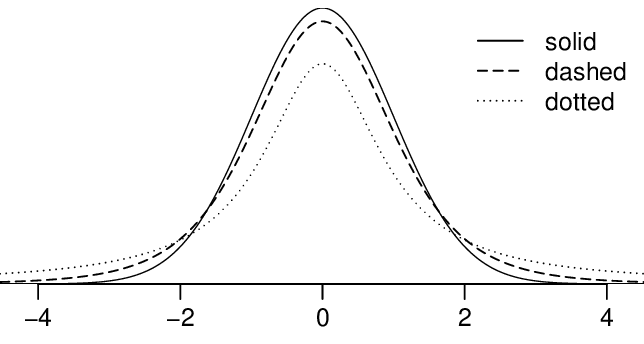
The \(t\)-distribution, always centered at zero, has a single parameter: degrees of freedom. The degrees of freedom (df) describes the precise form of the bell-shaped \(t\)-distribution. Several \(t\)-distributions are shown in Figure 7.1.2. When there are more degrees of freedom, the \(t\)-distribution looks more like the standard normal distribution.
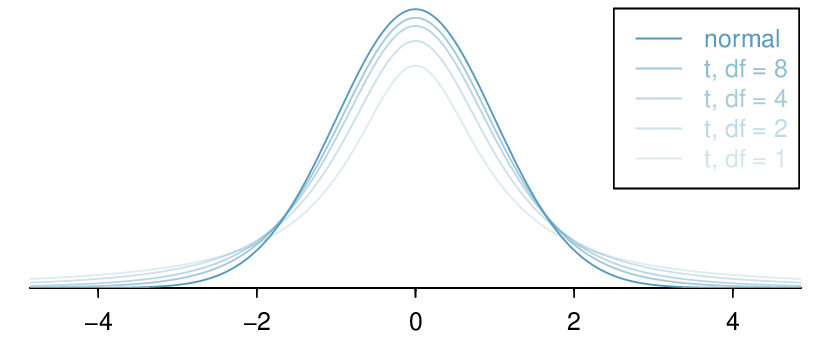
Degrees of freedom.
The degrees of freedom describes the shape of the \(t\)-distribution. The larger the degrees of freedom, the more closely the distribution resembles the standard normal distribution.
When the degrees of freedom is large, about 30 or more, the \(t\)-distribution is nearly indistinguishable from the normal distribution. In Subsection 7.1.5, we will see how degrees of freedom relates to sample size.
We will find it useful to become familiar with the \(t\)-distribution, because it plays a very similar role to the normal distribution during inference. We use a \(t\)-table, partially shown in Table 7.1.3, in place of the normal probability table when the population standard deviation is unknown, especially when the sample size is small. A larger table is presented in Section B.3.
| one tail | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | |
| \(df\) | 1 | 3.078 | 6.314 | 12.71 | 31.82 | 63.66 |
| 2 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | |
| 3 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| 17 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | |
| 18 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | |
| 19 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | |
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | ||
| 1000 | 1.282 | 1.646 | 1.962 | 2.330 | 2.581 | |
| \(\infty\) | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | |
| Confidence level C | 80% | 90% | 95% | 98% | 99% | |
Each row in the \(t\)-table represents a \(t\)-distribution with different degrees of freedom. The columns correspond to tail probabilities. For instance, if we know we are working with the \(t\)-distribution with \(df=18\text{,}\) we can examine row 18, which is highlighted in Table 7.1.3. If we want the value in this row that identifies the cutoff for an upper tail of 10%, we can look in the column where one tail is 0.100. This cutoff is 1.33. If we had wanted the cutoff for the lower 10%, we would use -1.33. Just like the normal distribution, all \(t\)-distributions are symmetric.
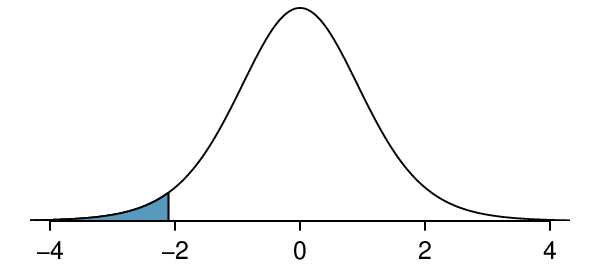
Example 7.1.4.
What proportion of the \(t\)-distribution with 18 degrees of freedom falls below -2.10?
Just like a normal probability problem, we first draw a picture as shown in Figure 7.1.5 and shade the area below -2.10. To find this area, we identify the appropriate row: \(df=18\text{.}\) Then we identify the column containing the absolute value of -2.10; it is the third column. Because we are looking for just one tail, we examine the top line of the table, which shows that a one tail area for a value in the third row corresponds to 0.025. That is, 2.5% of the distribution falls below -2.10.
Example 7.1.6.
For the \(t\)-distribution with 18 degrees of freedom, what percent of the curve is contained between -1.330 and +1.330?
Using row \(df = 18\text{,}\) we find 1.330 in the table. The area in each tail is 0.100 for a total of 0.200, which leaves 0.800 in the middle between -1.33 and +1.33. This corresponds to the 80%, which can be found at the very bottom of that column.
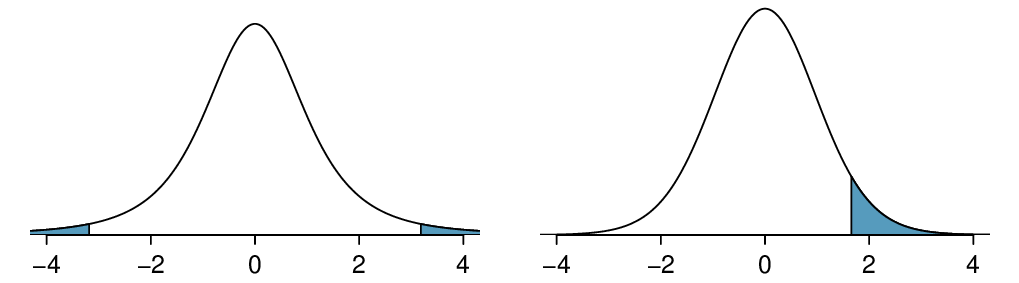
Example 7.1.7.
For the \(t\)-distribution with 3 degrees of freedom, as shown in the left panel of Figure 7.1.9, what should the value of \(t^{\star}\) be so that 95% of the area of the curve falls between -\(t^{\star}\) and +\(t^{\star}\text{?}\)
We can look at the column in the \(t\)-table that says 95% along the bottom row and trace it up to row \(df = 3\) to find that \(t^{\star} = 3.182\text{.}\)
Example 7.1.8.
A \(t\)-distribution with 20 degrees of freedom is shown in the right panel of Figure 7.1.9. Estimate the proportion of the distribution falling above 1.65.
We identify the row in the \(t\)-table using the degrees of freedom: \(df=20\text{.}\) Then we look for 1.65; it is not listed. It falls between the first and second columns. Since these values bound 1.65, their tail areas will bound the tail area corresponding to 1.65. We identify the one tail area of the first and second columns, 0.050 and 0.10, and we conclude that between 5% and 10% of the distribution is more than 1.65 standard deviations above the mean. If we like, we can identify the precise area using statistical software: 0.0573.
When the desired degrees of freedom is not listed on the table, choose a conservative value: round the degrees of freedom down, i.e. move up to the previous row listed. Another option is to use a calculator or statistical software to get a precise answer.
Subsection 7.1.4 Calculator: finding area under the \(t\)-distribution
It is possible to find areas under a \(t\)-distribution on a calculator.
TI-84: Finding area under the T-curve.
Use 2ND VARS, tcdf to find an area/proportion/probability between two \(t\)-scores or to the left or right of a \(t\)-score.
Choose
2NDVARS(i.e.DISTR).Choose
6:tcdf.-
Enter the
lower(left) \(t\)-score and theupper(right) \(t\)-score.If finding just a lower tail area, set
lowerto-100.For an upper tail area, set
upperto100.
Enter the degrees of freedom after
df:.Down arrow, choose
Paste, and hitENTER.
TI-83: Do steps 1-2, then enter the lower bound, upper bound, degrees of freedom, e.g. tcdf(2, 100, 5), and hit ENTER.
Casio fx-9750GII: Finding area under the T-distribution.
Navigate to
STAT(MENU, then hit2).Select
DIST(F5), thent(F2), and thentcd(F2).If needed, set
DatatoVariable(Varoption, which isF2).-
Enter the
Lower\(t\)-score and theUpper\(t\)-score. Set the degrees of freedom (df).If finding just a lower tail area, set
Lowerto-100.For an upper tail area, set
Upperto100.
Hit
EXE, which will return the area probability (p) along with the \(t\)-scores for the lower and upper bounds.
Checkpoint 7.1.10.
Use a calculator to find the area to the right of \(t=3\) under the \(t\)-distribution with 35 degrees of freedom. 1
lower \(= 3\text{.}\) There is no upper bound, so use a large value such as 100 for upper. Let df \(= 35\text{.}\) The area is 0.0025 or 0.25%.Checkpoint 7.1.11.
Without doing any calculations, will the area to the right of \(Z=3\) under the standard normal curve be greater than, less than, or equal to the area to the right of \(t=3\) with 35 degrees of freedom? 2
Subsection 7.1.5 Checking conditions for inference on a mean using the \(t\)-distribution
¶Using the \(t\)-distribution for inference on a mean requires two assumptions, namely that the observations are independent and that the theoretical sampling distribution of the sample mean \(\bar{x}\) is nearly normal. In practice, we check whether these assumptions are reasonable by verifying that certain conditions are met.
Independent. Observations can be considered independent when the data are collected from a random process, such as tossing a coin, or from a random sample. Without a random sample or process, the standard error formula would not apply, and it is unclear to what population the inference would apply. Recall from Chapter 6 that when sampling without replacement from a finite population, the observations can be considered independent when sampling less than 10% of the population.
Nearly normal sampling distribution. We saw in Section 4.2 that the sampling distribution of a sample mean will be nearly normal when the sample is drawn from a nearly normal population or when the sample size is at least 30 (\(n\ge 30\)).
What should we do when the sample size is small and we are not sure whether the population distribution is nearly normal? In this case, the best we can do is look at the data for excessive skew. If the data are very skewed or have obvious outliers, this suggests that the sample did not come from a nearly normal population. However, if the data do not show obvious skew or outliers, then the idea of a nearly normal population is generally considered reasonable, making the assumption of a nearly normal sampling distribution for \(\bar{x}\) reasonable as well.
Note that by looking at a small data set, we cannot prove that the population distribution is nearly normal. However, the data can suggest to us whether the population distribution being nearly normal is an unreasonable assumption.
The normality condition with small samples.
If the sample is small and there is strong skew or extreme outliers in the data, the population from which the sample was drawn may not be nearly normal.
Ideally, we use a graph of the data to check for strong skew or outliers. When the full data set is not available, summary statistics can also be used.
As the sample size goes up, it becomes less necessary to check for skew in the data. If the sample size is 30 or more, it is no longer necessary that the population distribution be nearly normal. When the sample size is large, the Central Limit Theorem tells us that the sampling distribution of the sample mean will be nearly normal regardless of the distribution of the population.
Subsection 7.1.6 One sample \(t\)-interval for a mean
¶Dolphins are at the top of the oceanic food chain, which causes dangerous substances such as mercury to concentrate in their organs and muscles. This is an important problem for both dolphins and other animals, like humans, who eat them.
We would like to create a confidence interval to estimate the average mercury content in dolphin muscles. We will use a sample of 19 Risso's dolphins from the Taiji area in Japan. The data are summarized in Table 7.1.13.
Because we are estimating a mean, we would like to construct a \(t\)-interval, but first we must check whether the conditions for using a \(t\)-interval are met. We will start by assuming that the sample of 19 Risso's dolphins constitutes a random sample. Next, we note that the sample size is small (less than 30), and we do not know whether the distribution of mercury content for all dolphins is nearly normal. Therefore, we must look at the data. Since we do not have all of the data to graph, we look at the summary statistics provided in Table 7.1.13. These summary statistics do not suggest any strong skew or outliers; all observations are within 2.5 standard deviations of the mean. Based on this evidence, we believe it is reasonable that the population distribution of mercury content in dolphins could be nearly normal.

| \(n\) | \(\bar{x}\) | \(s\) | minimum | maximum |
| 19 | 4.4 | 2.3 | 1.7 | 9.2 |
With both conditions met, we will construct a 95% confidence interval. Recall that a confidence interval has the following form:
The point estimate is the sample mean and the \(SE\) of the sample mean is given by \(s/\sqrt{n}\text{.}\) What do we use for the critical value? Since we are using the \(t\)-distribution, we use a \(t\)-table to find the critical value. We denote the critical value \(t^{\star}\text{.}\)
For a 95% confidence interval, we want to find the cutoff \(t^{\star}\) such that 95% of the \(t\)-distribution is between -\(t^{\star}\) and \(t^{\star}\text{.}\)
Using the \(t\)-table in Section B.3, we look at the row that corresponds to the degrees of freedom and the column that corresponds to the confidence level.
Degrees of freedom for a single sample.
If the sample has \(n\) observations and we are examining a single mean, then we use the \(t\)-distribution with \(df=n-1\) degrees of freedom.
Example 7.1.14.
Calculate a 95% confidence interval for the average mercury content in dolphin muscles based on this sample. Recall that \(n=19\text{,}\) \(\bar{x}=4.4\) \(\mu\)g/wet g, and \(s=2.3\) \(\mu\)g/wet g.
To find the critical value \(t^{\star}\) we use the \(t\)-distribution with \(n-1\) degrees of freedom. The sample size is 19, so \(df=19-1=18\) degrees of freedom. Using the \(t\)-table with row \(df=18\) and column corresponding to a 95% confidence level, we get \(t^{\star}=2.10\text{.}\) The point estimate is the sample mean \(\bar{x}\) and the standard error of a sample mean is given by \(\frac{s}{\sqrt{n}}\text{.}\) Now we have all the pieces we need to calculate a 95% confidence interval for the average mercury content in dolphin muscles.
Example 7.1.15.
How do we interpret this 95% confidence interval? To what population is it applicable?
A random sample of Risso's dolphins was taken from the Taiji area in Japan. The mercury content in the muscles of other types of dolphins and from dolphins from other regions may vary. Therefore, we can only make an inference to Risso's dolphins from this area. We are 95% confident the true average mercury content in the muscles of Risso's dolphins in the Taiji area of Japan is between 3.29 and 5.51 \(\mu\)g/wet gram.
Constructing a confidence interval for a mean.
To carry out a complete confidence interval procedure to estimate a single mean \(\mu\text{,}\)
Identify: Identify the parameter and the confidence level, C%.
The parameter will be an unknown population mean, e.g. the true mean (or average) mercury content in Risso's dolphins.
Choose: Choose the appropriate interval procedure and identify it by name.
Here we choose the 1-sample \(t\)-interval.
Check: Check conditions for the sampling distribution of \(\bar{x}\) to nearly normal.
Data come from a random sample or random process.
The sample size \(n\ge 30\) or the population distribution is nearly normal.
If the sample size is less than 30 and the population distribution is unknown, check for strong skew or outliers in the data. If neither is found, the condition that the population distribution is nearly normal is considered reasonable.
Calculate: Calculate the confidence interval and record it in interval form.
-
\(\text{ point estimate } \ \pm\ t^{\star} \times SE\ \text{ of estimate }\text{,}\) \(df = n - 1\)
point estimate: the sample mean \(\bar{x}\)
\(SE\) of estimate: \(\frac{s}{\sqrt{n}}\)
\(t^{\star}\text{:}\) use a \(t\)-table at row \(df = n-1\) and confidence level C
(, )
Conclude: Interpret the interval and, if applicable, draw a conclusion in context.
Here, we are C% confident that the true mean of [...] is between and . A conclusion depends upon whether the interval is entirely above, is entirely below, or contains the value of interest.
Example 7.1.16.
The FDA's webpage provides some data on mercury content of fish. 3 Based on a sample of 15 croaker white fish (Pacific), a sample mean and standard deviation were computed as 0.287 and 0.069 ppm (parts per million), respectively. The 15 observations ranged from 0.18 to 0.41 ppm. Construct an appropriate 95% confidence interval for the true average mercury content of croaker white fish (Pacific). Is there evidence that the average mercury content is greater than 0.275 ppm? Use the five step framework to organize your work.
Identify: The parameter of interest is the true mean mercury content in croaker white fish (Pacific). We want to estimate this at the 95% confidence level.
Choose: Because the parameter to be estimated is a single mean, we will use a 1-sample \(t\)-interval.
Check: We will assume that the sample constitutes a random sample of croaker white fish (Pacific). The sample size \(n\) is small, but there are no obvious outliers; all observations are within 2 standard deviations of the mean. If there is skew, it is not too great. Therefore we think it is reasonable that the population distribution of mercury content in croaker white fish (Pacific) could be nearly normal.
-
Calculate: We will calculate the interval:
\begin{gather*} \text{ point estimate } \ \pm\ t^{\star} \times SE\ \text{ of estimate } \end{gather*}The point estimate is the sample mean: \(\bar{x}= 0.287\)
The \(SE\) of the sample mean is: \(\frac{s}{\sqrt{n}} = \frac{0.069}{\sqrt{15}}\)
We find \(t^{\star}\) for the one sample case using the \(t\)-table at row \(df = n -1\) and confidence level C%. For a 95% confidence level and \(df = 15 - 1 = 14\text{,}\) \(t^{\star} = 2.145\text{.}\)
So the 95% confidence interval is given by:
\begin{align*} 0.287 \ \pm\ \amp 2.145\times \frac{0.069}{\sqrt{15}} \qquad df = 14\\ 0.287 \ \pm\ \amp 2.145\times 0.0178\\ =(0.2\amp 49,\ 0.325) \end{align*} Conclude: We are 95% confident that the true average mercury content of croaker white fish (Pacific) is between 0.249 and 0.325 ppm. Because the interval contains 0.275 as well as values less than 0.275, we do not have evidence that the true average mercury content is greater than 0.275 ppm.
Example 7.1.17.
Based on the interval calculated in Solution 7.1.16.1 above, can we say that 95% of croaker white fish (Pacific) have mercury content between 0.249 and 0.325 ppm?
No. The interval estimates the average amount of mercury with 95% confidence. It is not trying to capture 95% of the values.
Subsection 7.1.7 Calculator: the 1-sample \(t\)-interval
¶TI-83/84: 1-sample T-interval.
Use STAT, TESTS, TInterval.
Choose
STAT.Right arrow to
TESTS.Down arrow and choose
8:TInterval.-
Choose
Dataif you have all the data orStatsif you have the mean and standard deviation.If you choose
Data, letListbeL1or the list in which you entered your data (don't forget to enter the data!) and letFreqbe1.If you choose
Stats, enter the mean, \(SD\text{,}\) and sample size.
Let
C-Levelbe the desired confidence level.-
Choose
Calculateand hitENTER, which returns:(,) the confidence interval \(\bar{x}\) the sample mean Sxthe sample \(SD\) nthe sample size
Casio fx-9750GII: 1-sample T-interval.
Navigate to
STAT(MENUbutton, then hit the2button or selectSTAT).If necessary, enter the data into a list.
Choose the
INTRoption (F3button),t(F2button), and1-S(F1button).Choose either the
Varoption (F2) or enter the data in using theListoption.-
Specify the interval details:
Confidence level of interest for
C-Level.If using the
Varoption, enter the summary statistics. If usingList, specify the list and leaveFreqvalue at1.
-
Hit the
EXEbutton, which returnsLeft,Rightends of the confidence interval \(\bar{x}\) sample mean sxsample standard deviation nsample size
Checkpoint 7.1.18.
Use a calculator to find a 95% confidence interval for the mean mercury content in croaker white fish (Pacific). The sample size was 15, and the sample mean and standard deviation were computed as 0.287 and 0.069 ppm (parts per million), respectively. 4
TInterval or equivalent. We do not have all the data, so choose Stats on a TI or Var on a Casio. Enter x and Sx. Note: Sx is the sample standard deviation (0.069), not the \(SE\text{.}\) Let \(n = 15\) and C-Level \(= 0.95\text{.}\) This should give the interval (0.249, 0.325).Subsection 7.1.8 Choosing a sample size when estimating a mean
¶In Subsection 6.1.6, we looked at sample size considerations when estimating a proportion. We take the same approach when estimating a mean. Recall that the margin of error is measured as the distance between the point estimate and the upper or lower bound of the confidence interval. We want to estimate a mean with a particular confidence level while putting an upper bound on the margin of error. What is the smallest sample size that will satisfy these conditions?
For a one sample \(t\)-interval, the margin of error, \(ME\text{,}\) is given by \(ME = t^{\star}\times\frac{s}{\sqrt{n}}\text{.}\) The challenge in this case is that we need to know \(n\) to find \(t^{\star}\text{.}\) But \(n\) is precisely what we are attempting to solve for! Fortunately, in most cases we will have a reasonable estimate for the population standard deviation and the desired \(n\) will be large, so we can use \(ME = z^{\star}\times\frac{\sigma}{\sqrt{n}}\text{,}\) making it easier to solve for \(n\text{.}\)
Example 7.1.19.
Blood pressure oscillates with the beating of the heart, and the systolic pressure is defined as the peak pressure when a person is at rest. The standard deviation of systolic blood pressure for people in the U.S. is about 25 mmHg (millimeters of mercury). How large of a sample is necessary to estimate the average systolic blood pressure of people in a particular town with a margin of error no greater than 4 mmHg using a 95% confidence level?
For this problem, we want to find the sample size \(n\) so that the margin of error, \(ME\text{,}\) is less than or equal to 4 mmHg. We start by writing the following inequality:
For a 95% confidence level, the critical value \(z^{\star}=1.96\text{.}\) Our best estimate for the population standard deviation is \(\sigma = 25\text{.}\) We substitute in these two values and we solve for \(n\text{.}\)
The minimum sample size that meets the condition is 151. We round up because the sample size must be an integer and it must be greater than or equal to 150.06.
Identify a sample size for a particular margin of error.
To estimate the minimum sample size required to achieve a margin of error less than or equal to \(m\text{,}\) with C% confidence, we set up an inequality as follows:
\(z^{\star}\) depends on the desired confidence level and \(\sigma\) is the standard deviation associated with the population. We solve for the sample size, \(n\text{.}\)
Sample size computations are helpful in planning data collection, and they require careful forethought.
Subsection 7.1.9 Hypothesis testing for a mean
¶Is the typical U.S. runner getting faster or slower over time? Technological advances in shoes, training, and diet might suggest runners would be faster. An opposing viewpoint might say that with the average body mass index on the rise, people tend to run slower. In fact, all of these components might be influencing run time.
We consider this question in the context of the Cherry Blossom Race, which is a 10-mile race in Washington, DC each spring. The average time for all runners who finished the Cherry Blossom Race in 2006 was 93.3 minutes (93 minutes and about 18 seconds). We want to determine using data from 100 participants in the 2017 Cherry Blossom Race whether runners in this race are getting faster or slower, versus the other possibility that there has been no change. Figure 7.1.20 shows run times for 100 randomly selected participants.
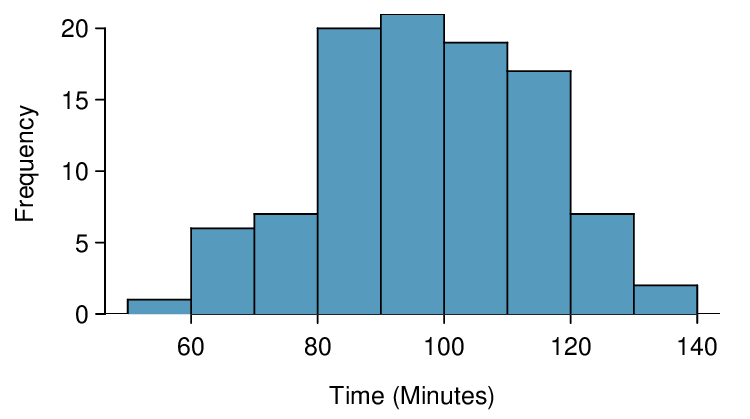
time for the sample of 2017 Cherry Blossom Race participants.Example 7.1.21.
What are appropriate hypotheses for this context?
We know that the average run time for all runners in 2006 was 93.3 minutes. We have a sample of times from the 2017 race. We are interested in whether the average run time has changed, so we will use a two-sided \(H_A\text{.}\)
Let \(\mu\) represent the average 10-mile run time of all participants in 2017,which is unknown to us.
\(H_0\text{:}\) \(\mu = 93.3\) minutes. The average run time of all participants in 2017 was 93.3 min.
\(H_A\text{:}\) \(\mu \neq 93.3\) minutes. The average run time of all participants in 2017 was not 93.3 min.
The data come from a random sample from a large population, so the observations are independent. Do we need to check for skew in the data? No — with a sample size of 100, well over 30, the Central Limit Theorem tells us that the sampling distribution of \(\bar{x}\) will be nearly normal.
With independence satisfied and slight skew not a concern for this large of a sample, we can proceed with performing a hypothesis test using the \(t\)-distribution.
The sample mean and sample standard deviation of the 100 runners from the 2017 Cherry Blossom Race are 97.3 and 17.0 minutes, respectively. We want to know whether the observed sample mean of 97.3 is far enough away from 93.3 to provide convincing evidence of a real difference, or if it is within the realm of expected variation for a sample of size 100.
To answer this question we will find the test statistic and p-value for the hypothesis test. Since we will be using a sample standard deviation in our calculation of the test statistic, we will need to use a \(t\)-distribution, just as we did with confidence intervals for a mean. We call the test statistic a \(T\)-statistic. It has the same general form as a Z-statistic.
As we saw before, when carrying out inference on a single mean, the degrees of freedom is given by \(n-1\text{.}\)
The T-statistic.
The T-statistic (or T-score) is analogous to a Z-statistic (or Z-score). Both represent how many standard errors the observed value is from the null value.
Example 7.1.22.
Calculate the test statistic, degrees of freedom, and p-value for this test.
Here, our point estimate is the sample mean, \(\bar{x}=97.3\) minutes.
The \(SE\) of the sample mean is given by \(\frac{s}{\sqrt{n}}\text{,}\) so the \(SE\) of estimate = \(\frac{17}{\sqrt{100}} = 1.7\) minutes.
Using a calculator, we find that the area above 2.35 under the \(t\)-distribution with 99 degrees of freedom is 0.01. Because this is a two-tailed test, we double this. So the p-value = \(2\times 0.01 = 0.02\text{.}\)
Example 7.1.23.
Does the data provide sufficient evidence that the average Cherry Blossom Run time in 2017 is different than in 2006?
This depends upon the desired significance level. Since the p-value \(= 0.02 \lt 0.05\text{,}\) there is sufficient evidence at the 5% significance level. However, as the p-value of \(0.02 \gt 0.01\text{,}\) there is not sufficient evidence at the 1% significance level.
Example 7.1.24.
Would you expect the hypothesized value of 93.3 to fall inside or outside of a 95% confidence interval? What about a 99% confidence interval?
Because the hypothesized value of 93.3 was rejected by the two-sided \(\alpha=0.05\) test, we would expect it to be outside the 95% confidence interval. However, because the hypothesized value of 93.3 was not rejected by the two-sided \(\alpha=0.01\) test, we would expect it to fall inside the (wider) 99% confidence interval.
Hypothesis test for a mean.
To carry out a complete hypothesis test to test the claim that a single mean \(\mu\) is equal to a null value \(\mu_0\text{,}\)
Identify: Identify the hypotheses and the significance level, \(\alpha\text{.}\)
\(H_0\text{:}\) \(\mu = \mu_0\)
\(H_A\text{:}\) \(\mu \ne \mu_0\text{;}\) \(H_A\text{:}\) \(\mu > \mu_0\text{;}\) or \(H_A\text{:}\) \(\mu \lt \mu_0\)
Choose: Choose the appropriate test procedure and identify it by name.
Here we choose the 1-sample \(t\)-test.
Check: Check conditions for the sampling distribution of \(\bar{x}\) to be nearly normal.
Data come from a random sample or random process.
The sample size \(n\ge 30\) or the population distribution is nearly normal.
If the sample size is less than 30 and the population distribution is unknown, check for strong skew or outliers in the data. If neither is found, then the condition that the population is nearly normal is considered reasonable.
Calculate: Calculate the \(t\)-statistic, \(df\text{,}\) and p-value.
-
\(T = \frac{\text{ point estimate } - \text{ null value } }{SE \text{ of estimate } }\text{,}\) \(df=n-1\)
point estimate: the sample mean \(\bar{x}\)
\(SE\) of estimate: \(\frac{s}{\sqrt{n}}\)
null value: \(\mu_0\)
p-value = (based on the \(t\)-statistic, the \(df\text{,}\) and the direction of \(H_A\))
Conclude: Compare the p-value to \(\alpha\text{,}\) and draw a conclusion in context.
If the p-value is \(\lt \alpha\text{,}\) reject \(H_0\text{;}\) there is sufficient evidence that [\(H_A\) in context].
If the p-value is \(> \alpha\text{,}\) do not reject \(H_0\text{;}\) there is not sufficient evidence that [\(H_A\) in context].
Example 7.1.25.
Recall the example involving the mercury content in croaker white fish (Pacific). Based on a sample of size 15, a sample mean and standard deviation were computed as 0.287 and 0.069 ppm (parts per million), respectively. Carry out an appropriate test to determine if 0.25 is a reasonable value for the average mercury content of croaker white fish (Pacific). Use the five step method to organize your work.
Identify: We will test the following hypotheses at the \(\alpha=0.05\) significance level.
\(H_0\text{:}\) \(\mu=0.25\)
\(H_A\text{:}\) \(\mu \ne 0.25\) The mean mercury content is not 0.25 ppm.
Choose: Because we are hypothesizing about a single mean we choose the 1-sample \(t\)-test.
Check: The conditions were checked previously, namely — the data come from a random sample, and because \(n\) is less than 30, we verified that there is no strong skew or outliers in the data, so the assumption that the population distribution of mercury is nearly normally distributed is reasonable.
Calculate: We will calculate the \(t\)-statistic and the p-value.
The point estimate is the sample mean: \(\bar{x}\) = 0.287
The \(SE\) of the sample mean is: \(\frac{s}{\sqrt{n}} = \frac{0.069}{\sqrt{15}} = 0.0178\)
The null value is the value hypothesized for the parameter in \(H_0\text{,}\) which is 0.25.
For the 1-sample \(t\)-test, \(df = n-1\text{.}\)
Because \(H_A\) is a two-tailed test ( \(\ne\) ), the p-value corresponds to the area to the right of \(t=2.07\) plus the area to the left of \(t=-2.07\) under the \(t\)-distribution with 14 degrees of freedom. The p-value = \(2\times 0.029 = 0.058\text{.}\)
Conclude: The p-value of \(0.058 > 0.05\text{,}\) so we do not reject the null hypothesis. We do not have sufficient evidence that the average mercury content in croaker white fish (Pacific) is not 0.25.
Checkpoint 7.1.26.
Recall that the 95% confidence interval for the average mercury content in croaker white fish was (0.249, 0.325). Discuss whether the conclusion of the hypothesis test in the previous example is consistent or inconsistent with the conclusion of the confidence interval. 5
Subsection 7.1.10 Calculator: 1-sample \(t\)-test
¶TI-83/84: 1-sample T-test.
Use STAT, TESTS, T-Test.
Choose
STAT.Right arrow to
TESTS.Down arrow and choose
2:T-Test.Choose
Dataif you have all the data orStatsif you have the mean and standard deviation.-
Let \(\mu_0\) be the null or hypothesized value of \(\mu\text{.}\)
If you choose
Data, letListbeL1or the list in which you entered your data (don't forget to enter the data!) and letFreqbe1.If you choose
Stats, enter the mean, \(SD\text{,}\) and sample size.
Choose \(\ne\text{,}\) \(\lt\text{,}\) or > to correspond to \(H_A\text{.}\)
-
Choose
Calculateand hitENTER, which returns:tt statistic Sxthe sample standard deviation pp-value nthe sample size \(\bar{x}\) the sample mean
Casio fx-9750GII: 1-sample T-test.
Navigate to
STAT(MENUbutton, then hit the2button or selectSTAT).If necessary, enter the data into a list.
Choose the
TESToption (F3button).Choose the
toption (F2button).Choose the
1-Soption (F1button).Choose either the
Varoption (F2) or enter the data in using theListoption.-
Specify the test details:
Specify the sidedness of the test using the
F1,F2, andF3keys.Enter the null value, \(\mu\)
0.If using the
Varoption, enter the summary statistics. If usingList, specify the list and leaveFreqvalues at1.
-
Hit the
EXEbutton, which returnsalternative hypothesis \(\bar{x}\) sample mean tT statistic sxsample standard deviation pp-value nsample size
Checkpoint 7.1.27.
The average time for all runners who finished the Cherry Blossom Run in 2006 was 93.3 minutes. In 2017, the average time for 100 randomly selected participants was 97.3, with a standard deviation of 17.0 minutes. Use a calculator to find the \(T\)-statistic and p-value for the appropriate test to see if the average time for the participants in 2017 is different than it was in 2006. 6
T-Test or equivalent. Let \(\mu{0}\) be 93.3. x is 97.3, \(S_{x}\) is 17.0 and n \(=100\text{.}\) Choose \(\ne\) to correspond to \(H_{A}\text{.}\) We get t\(=2.353\) and the p-value p\(=0.021\)Subsection 7.1.11 Section summary
-
The \(t\)-distribution.
When calculating a test statistic for a mean, using the sample standard deviation in place of the population standard deviation gives rise to a new distribution called the \(t\)-distribution.
As the sample size and degrees of freedom increase, \(s\) becomes a more stable estimate of \(\sigma\text{,}\) and the corresponding \(t\)-distribution has smaller spread.
As the degrees of freedom go to \(\infty\text{,}\) the \(t\)-distribution approaches the normal distribution. This is why we can use the \(t\)-table at \(df=\infty\) to find the value of \(z^{\star}\text{.}\)
When carrying out inference for a single mean, we use the \(t\)-distribution with \(n-1\) degrees of freedom.
-
When there is one sample and the parameter of interest is a single mean:
Estimate \(\mu\) at the C% confidence level using a 1-sample t-interval.
Test \(H_0\text{:}\) \(\mu=\mu_0\) at the \(\alpha\) significance level using a 1-sample t-test.
-
The conditions for the one sample \(t\)-interval and \(t\)-test are the same.
The data come from a random sample or random process.
The sample size \(n\ge 30\) or the population distribution is nearly normal. If the sample size is less than 30 and the population distribution is unknown, check for strong skew or outliers in the data. If neither is found, then the condition that the population distribution is nearly normal is considered reasonable.
-
When the conditions are met, we calculate the confidence interval and the test statistic as we did in the previous chapter, except that we use \(t^{\star}\) for the critical value and we use \(T\) for the test statistic.
Confidence interval: \(\text{ point estimate } \ \pm\ t^{\star} \times SE\ \text{ of estimate }\)
Test statistic: \(T = \frac{\text{ point estimate } - \text{ null value } }{SE \text{ of estimate } }\)
Here the point estimate is the sample mean: \(\bar{x}\text{.}\)
The \(SE\) of estimate is the \(SE\) of the sample mean: \(\frac{s}{\sqrt{n}}\text{.}\)
The degrees of freedom is given by \(df = n-1\text{.}\)
-
To calculate the minimum sample size required to estimate a mean with C% confidence and a margin of error no greater than \(m\text{,}\) we set up an inequality as follows:
\begin{gather*} z^{\star}\frac{\sigma}{\sqrt{n}}\leq m \end{gather*}\(z^{\star}\) depends on the desired confidence level and \(\sigma\) is the standard deviation associated with the population. We solve for the sample size, \(n\text{.}\) Always round the answer up to the next integer, since \(n\) refers to a number of people or things.
Exercises 7.1.12 Exercises
1. Identify the critical \(t\).
An independent random sample is selected from an approximately normal population with unknown standard deviation. Find the degrees of freedom and the critical \(t\)-value (t\(^\star\)) for the given sample size and confidence level.
\(n = 6\text{,}\) CL = 90
\(n = 21\text{,}\) CL = 98
\(n = 29\text{,}\) CL = 95
\(n = 12\text{,}\) CL = 99
(a) \(df = 6 - 1 = 5\text{,}\) \(t^{*}_{5} = 2.02\) (column with two tails of 0.10, row with \(df = 5\)).
(b) \(df = 21-1 = 20\text{,}\) \(t^{*}_{20} = 2.53\) (column with two tails of 0.02, row with \(df = 20\)).
(c) \(df = 28\text{,}\) \(t^{*}_{28} = 2.05\text{.}\)
(d) \(df = 11\text{,}\) \(t^{*}_{11} = 3.11\text{.}\)
2. \(t\)-distribution.
The figure on the right shows three unimodal and symmetric curves: the standard normal (\(z\)) distribution, the \(t\)-distribution with 5 degrees of freedom, and the \(t\)-distribution with 1 degree of freedom. Determine which is which, and explain your reasoning.
3. Find the p-value, Part I.
An independent random sample is selected from an approximately normal population with an unknown standard deviation. Find the p-value for the given sample size and test statistic. Also determine if the null hypothesis would be rejected at \(\alpha = 0.05\text{.}\)
\(n = 11\text{,}\) \(T = 1.91\)
\(n = 17\text{,}\) \(T = -3.45\)
\(n = 7\text{,}\) \(T = 0.83\)
\(n = 28\text{,}\) \(T = 2.13\)
(a) 0.085, do not reject H0.
(b) 0.003, reject \(H_{0}\text{.}\)
(c) 0.438, do not reject H0.
(d) 0.042, reject \(H_{0}\text{.}\)
4. Find the p-value, Part II.
An independent random sample is selected from an approximately normal population with an unknown standard deviation. Find the p-value for the given sample size and test statistic. Also determine if the null hypothesis would be rejected at \(\alpha = 0.01\text{.}\)
\(n = 26\text{,}\) \(T = 2.485\)
\(n = 18\text{,}\) \(T = 0.5\)
5. Working backwards, Part I.
A 95% confidence interval for a population mean, \(\mu\text{,}\) is given as (18.985, 21.015). This confidence interval is based on a simple random sample of 36 observations. Calculate the sample mean and standard deviation. Assume that all conditions necessary for inference are satisfied. Use the \(t\)-distribution in any calculations.
The mean is the midpoint: \(bar{x} = 20\text{.}\) Identify the margin of error: \(ME = 1.015\text{,}\) then use \(t^{*}_{35} = 2.03\) and \(SE = s/ \sqrt{n}\) in the formula for margin of error to identify \(s = 3\text{.}\)
6. Working backwards, Part II.
A 90% confidence interval for a population mean is (65, 77). The population distribution is approximately normal and the population standard deviation is unknown. This confidence interval is based on a simple random sample of 25 observations. Calculate the sample mean, the margin of error, and the sample standard deviation.
7. Sleep habits of New Yorkers.
New York is known as “the city that never sleeps”. A random sample of 25 New Yorkers were asked how much sleep they get per night. Statistical summaries of these data are shown below. The point estimate suggests New Yorkers sleep less than 8 hours a night on average. Is the result statistically significant?
| n | \(\bar{x}\) | s | min | max | |
| 25 | 7.73 | 0.77 | 6.17 | 9.78 | |
Write the hypotheses in symbols and in words.
Check conditions, then calculate the test statistic, \(T\text{,}\) and the associated degrees of freedom.
Find and interpret the p-value in this context. Drawing a picture may be helpful.
What is the conclusion of the hypothesis test?
If you were to construct a 90% confidence interval that corresponded to this hypothesis test, would you expect 8 hours to be in the interval?
(a) \(H_{0}: \mu = 8\) (New Yorkers sleep 8 hrs per night on average.) \(H_{A}: \mu \ne 8\) (New Yorkers sleep less or more than 8 hrs per night on average.)
(b) Independence: The sample is random. The min/max suggest there are no concerning outliers. \(T = -1.75\text{.}\) \(df = 25 - 1 = 24\text{.}\)
(c) \(\text{p-value } = 0.093\text{.}\) If in fact the true population mean of the amount New Yorkers sleep per night was 8 hours, the probability of getting a random sample of 25 New Yorkers where the average amount of sleep is 7.73 hours per night or less (or 8.27 hours or more) is 0.093.
(d) Since \(\text{p-value } > 0.05\text{,}\) do not reject \(H_{0}\text{.}\) The data do not provide strong evidence that New Yorkers sleep more or less than 8 hours per night on average.
(e) Yes, since we did not rejected \(H_{0}\text{.}\)
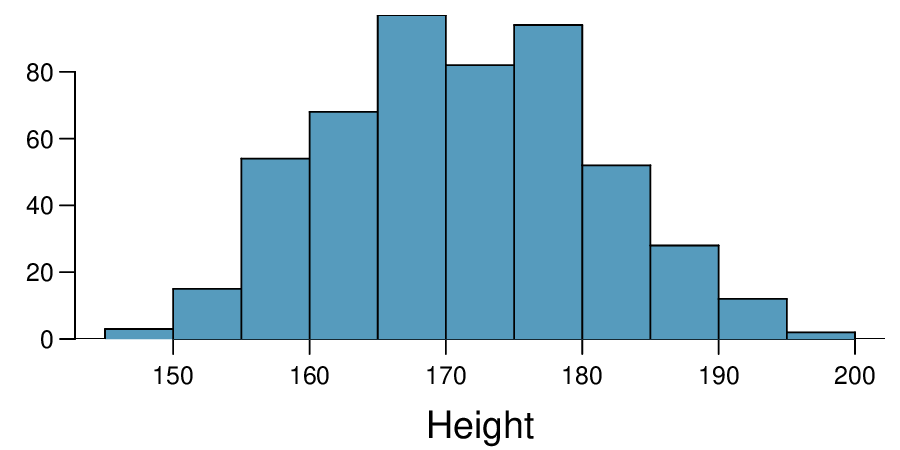
8. Heights of adults.
Researchers studying anthropometry collected body girth measurements and skeletal diameter measurements, as well as age, weight, height and gender, for 507 physically active individuals. The histogram below shows the sample distribution of heights in centimeters. 7
| Min | 147.2 |
| Q1 | 163.8 |
| Median | 170.3 |
| Mean | 171.1 |
| SD | 9.4 |
| Q3 | 177.8 |
| Max | 198.1 |
What is the point estimate for the average height of active individuals? What about the median?
What is the point estimate for the standard deviation of the heights of active individuals? What about the IQR?
Is a person who is 1m 80cm (180 cm) tall considered unusually tall? And is a person who is 1m 55cm (155cm) considered unusually short? Explain your reasoning.
The researchers take another random sample of physically active individuals. Would you expect the mean and the standard deviation of this new sample to be the ones given above? Explain your reasoning.
The sample means obtained are point estimates for the mean height of all active individuals, if the sample of individuals is equivalent to a simple random sample. What measure do we use to quantify the variability of such an estimate? Compute this quantity using the data from the original sample under the condition that the data are a simple random sample.
9. Find the mean.
You are given the following hypotheses:
We know that the sample standard deviation is 8 and the sample size is 20. For what sample mean would the p-value be equal to 0.05? Assume that all conditions necessary for inference are satisfied.
\(T\) is either -2.09 or 2.09. Then \(\bar{x}\) is one of the following:
10. \(t^\star\) vs. \(z^\star\).
For a given confidence level, \(t^{\star}_{df}\) is larger than \(z^{\star}\text{.}\) Explain how \(t^{*}_{df}\) being slightly larger than \(z^{*}\) affects the width of the confidence interval.
11. Play the piano.
Georgianna claims that in a small city renowned for its music school, the average child takes at least 5 years of piano lessons. We have a random sample of 30 children from the city, with a mean of 4.6 years of piano lessons and a standard deviation of 2.2 years.
Use a hypothesis test to determine if there is sufficient evidence against Georgianna's claim.
Construct a 95% confidence interval for the number of years students in this city take piano lessons, and interpret it in context of the data.
Do your results from the hypothesis test and the confidence interval agree? Explain your reasoning.
(a) We will conduct a 1-sample t-test. \(H_{0}: \mu = 5\text{.}\) \(H_{A}: \mu < 5\text{.}\) We'll use \(\sigma = 0.05\text{.}\) This is a random sample, so the observations are independent. To proceed, we assume the distribution of years of piano lessons is approximately normal. \(SE = 2.2/ \sqrt{30} = 0.402\text{.}\) The test statistic is \(T = (4.6 - 5)/SE = -0.995\text{.}\) \(df = 30 - 1 = 29\text{.}\) The p-value is about 0.164, which is bigger than \(\sigma = 0.05\) and we do not reject \(H_{0}\text{.}\) That is, we do not have sufficiently strong evidence to reject Georgianna's claim that the average is (at least) 5 years.
(b) Using \(SE = 0.402\) and \(t^{*}_{df=29} = 2.045\text{,}\) the confidence interval is \((3.78, 5.42)\text{.}\) We are 95% confident that the average number of years a child takes piano lessons in this city is between 3.78 and 5.42 years.
(c) They agree, since we did not reject the null hypothesis and the null value of 5 was in the \(t\)-interval.
12. Auto exhaust and lead exposure.
Researchers interested in lead exposure due to car exhaust sampled the blood of 52 police officers subjected to constant inhalation of automobile exhaust fumes while working traffic enforcement in a primarily urban environment. The blood samples of these officers had an average lead concentration of 124.32 \(\mu\)g/l and a SD of 37.74 \(\mu\)g/l; a previous study of individuals from a nearby suburb, with no history of exposure, found an average blood level concentration of 35 \(\mu\)g/l. 8
Write down the hypotheses that would be appropriate for testing if the police officers appear to have been exposed to a different concentration of lead.
Explicitly state and check all conditions necessary for inference on these data.
Regardless of your answers in part (b), test the hypothesis that the downtown police officers have a higher lead exposure than the group in the previous study. Interpret your results in context.
13. Car insurance savings.
A market researcher wants to evaluate car insurance savings at a competing company. Based on past studies he is assuming that the standard deviation of savings is $100. He wants to collect data such that he can get a margin of error of no more than $10 at a 95% confidence level. How large of a sample should he collect?
Assuming the population standard deviation is known, the margin of error will be \(1.96 \times 100/ \sqrt{n}\text{.}\) We want this value to be less than 10, which leads to \(n \gt 384.16\text{,}\) meaning we need a sample size of at least 385 (round up for sample size calculations!).
14. SAT scores.
The standard deviation of SAT scores for students at a particular Ivy League college is 250 points. Two statistics students, Raina and Luke, want to estimate the average SAT score of students at this college as part of a class project. They want their margin of error to be no more than 25 points.
Raina wants to use a 90% confidence interval. How large a sample should she collect?
Luke wants to use a 99% confidence interval. Without calculating the actual sample size, determine whether his sample should be larger or smaller than Raina's, and explain your reasoning.
Calculate the minimum required sample size for Luke.
