Section 1.5 Experiments
¶You would like to determine if drinking a cup of tea each morning will cause students to perform better on tests. What are different ways you could design an experiment to answer this question? What are possible sources of bias, and how would you try to minimize them? The goal of an experiment is to be able to draw a causal conclusion about the effect of a treatment — in this case, drinking tea. If the design is poor, a causal conclusion cannot be drawn, even if you observe an association between drinking tea and performing better on tests. This is why it is crucial to start with a well-designed experiment.
Subsection 1.5.1 Learning objectives
Identify the subjects/experimental units, treatments, and response variable in an experiment.
Identify the three main principles of experiment design and explain their purpose: direct control, randomization, and replication.
Explain placebo effect and describe when and how to implement a single-blind and a double-blind experiment.
Identify and describe how to implement the following three experimental designs: completely randomized design, blocked design, and matched pairs design.
Explain the purpose of random assignment or randomization in each of the three experimental designs.
Explain how to randomize treatments in a completely randomized design using technology or a table of random digits (make sure this is explained).
Explain when it is reasonable to draw a causal conclusion about the effect of a treatment.
Identify the number of factors in experiment, the number of levels for each factor and the total number of treatments.
Subsection 1.5.2 Reducing bias in human experiments
¶In the last section we investigated observational studies and sampling strategies. While these are effective tools for answering certain research questions, often times researchers want to measure the effect of a treatment. In this case, they must carry out an experiment. Just as randomization is essential in sampling in order to avoid selection bias, randomization is essential in the context of experiments to determine which subjects will receive which treatments. If the researcher chooses which patients are in the treatment and control groups, she may unintentionally place sicker patients in the treatment group, biasing the experiment against the treatment.
Randomized experiments are essential for investigating cause and effect relationships, but they do not ensure an unbiased perspective in all cases. Human studies are perfect examples where bias can unintentionally arise. Here we reconsider a study where a new drug was used to treat heart attack patients. 1 In particular, researchers wanted to know if the drug reduced deaths in patients.
These researchers designed a randomized experiment because they wanted to draw causal conclusions about the drug's effect. Study volunteers 2 were randomly placed into two study groups. One group, the treatment group, received the drug. The other group, called the control group, did not receive any drug treatment. In an experiment, the explanatory variable is also called a factor. Here the factor is receiving the drug treatment. It has two levels: yes and no, thus it is categorical. The response variable is whether or not patients died within the time frame of the study. It is also categorical.
Put yourself in the place of a person in the study. If you are in the treatment group, you are given a fancy new drug that you anticipate will help you. On the other hand, a person in the other group doesn't receive the drug and sits idly, hoping her participation doesn't increase her risk of death. These perspectives suggest there are actually two effects: the one of interest is the effectiveness of the drug, and the second is an emotional effect that is difficult to quantify.
Researchers aren't usually interested in the emotional effect, which might bias the study. To circumvent this problem, researchers do not want patients to know which group they are in. When researchers keep the patients uninformed about their treatment, the study is said to be blind or single-blind. But there is one problem: if a patient doesn't receive a treatment, she will know she is in the control group. The solution to this problem is to give fake treatments to patients in the control group. A fake treatment is called a placebo, and an effective placebo is the key to making a study truly blind. A classic example of a placebo is a sugar pill that is made to look like the actual treatment pill. Often times, a placebo results in a slight but real improvement in patients. This effect has been dubbed the placebo effect.
The patients are not the only ones who should be blinded: doctors and researchers can accidentally bias a study. When a doctor knows a patient has been given the real treatment, she might inadvertently give that patient more attention or care than a patient that she knows is on the placebo. To guard against this bias, which again has been found to have a measurable effect in some instances, most modern studies employ a double-blind setup where researchers who interact with subjects and are responsible for measuring the response variable are, just like the subjects, unaware of who is or is not receiving the treatment. 3
Checkpoint 1.5.1.
Look back to the study in Section 1.1 where researchers were testing whether stents were effective at reducing strokes in at-risk patients. Is this an experiment? Was the study blinded? Was it double-blinded? 4
Subsection 1.5.3 Principles of experimental design
¶Well-conducted experiments are built on three main principles.
-
Direct Control. Researchers assign treatments to cases, and they do their best to control any other differences in the groups. They want the groups to be as identical as possible except for the treatment, so that at the end of the experiment any difference in response between the groups can be attributed to the treatment and not to some other confounding or lurking variable. For example, when patients take a drug in pill form, some patients take the pill with only a sip of water while others may have it with an entire glass of water. To control for the effect of water consumption, a doctor may ask all patients to drink a 12 ounce glass of water with the pill.
Direct control refers to variables that the researcher can control, or make the same. A researcher can directly control the appearance of the treatment, the time of day it is taken, etc. She cannot directly control variables such as gender or age. To control for these other types of variables, she might consider blocking, which is described in Subsection 1.5.4.
Randomization. Researchers randomize patients into treatment groups to account for variables that cannot be controlled. For example, some patients may be more susceptible to a disease than others due to their dietary habits. Randomizing patients into the treatment or control group helps even out the effects of such differences, and it also prevents accidental bias from entering the study.
Replication. The more cases researchers observe, the more accurately they can estimate the effect of the explanatory variable on the response. In an experiment with six subjects, even if there is randomization, it is quite possible for the three healthiest people to be in the same treatment group. In a randomized experiment with 100 people, it is virtually impossible for the healthiest 50 people to end up in the same treatment group. In a single study, we replicate by imposing the treatment on a sufficiently large number of subjects or experimental units. A group of scientists may also replicate an entire study to verify an earlier finding. However, each study should ensure a sufficiently large number of subjects because, in many cases, there is no opportunity or funding to carry out the entire experiment again.
It is important to incorporate these design principles into any experiment. If they are lacking, the inference methods presented in the following chapters will not be applicable and their results may not be trustworthy. In the next section we will consider three types of experimental design.
Subsection 1.5.4 Completely randomized, blocked, and matched pairs design
¶A completely randomized experiment is one in which the subjects or experimental units are randomly assigned to each group in the experiment. Suppose we have three treatments, one of which may be a placebo, and 300 subjects. To carry out a completely randomized design, we could randomly assign each subject a unique number from 1 to 300, then subjects with numbers 1-100 would get treatment 1, subjects 101-200 would get treatment 2, and subjects 201- 300 would get treatment 3. Note that this method of randomly allocating subjects to treatments in not equivalent to taking a simple random sample. Here we are not sampling a subset of a population; we are randomly splitting subjects into groups.
While it might be ideal for the subjects to be a random sample of the population of interest, that is rarely the case. Subjects must volunteer to be part of an experiment. However, because randomization is incorporated in the splitting of the groups, we can still use statistical techniques to check for a causal connection, though the precise population for which the conclusion applies may be unclear. For example, if an experiment to determine the most effective means to encourage individuals to vote is carried out only on college students, we may not be able to generalize the conclusions of the experiment to all adults in the population.
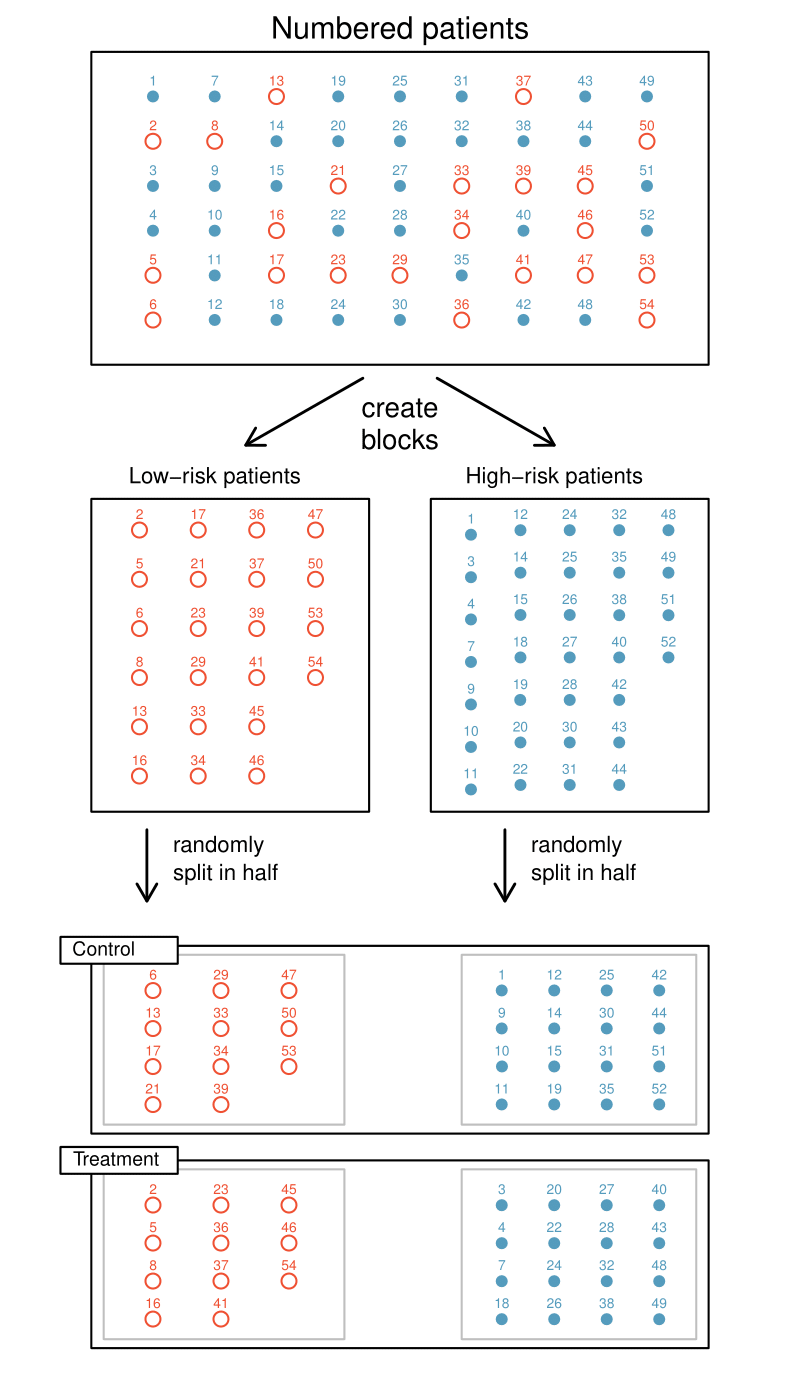
Researchers sometimes know or suspect that another variable, other than the treatment, influences the response. Under these circumstances, they may carry out a blocked experiment. In this design, they first group individuals into blocks based on the identified variable and then randomize subjects within each block to the treatment groups. This strategy is referred to as blocking. For instance, if we are looking at the effect of a drug on heart attacks, we might first split patients in the study into low-risk and high-risk blocks. Then we can randomly assign half the patients from each block to the control group and the other half to the treatment group, as shown in Figure 1.5.2. At the end of the experiment, we would incorporate this blocking into the analysis. By blocking by risk of patient, we control for this possible confounding factor. Additionally, by randomizing subjects to treatments within each block, we attempt to even out the effect of variables that we cannot block or directly control.
Example 1.5.3.
An experiment will be conducted to compare the effectiveness of two methods for quitting smoking. Identify a variable that the researcher might wish to use for blocking and describe how she would carry out a blocked experiment.
The researcher should choose the variable that is most likely to influence the response variable - whether or not a smoker will quit. A reasonable variable, therefore, would be the number of years that the smoker has been smoking. The subjects could be separated into three blocks based on number of years of smoking and each block randomly divided into the two treatment groups.
Even in a blocked experiment with randomization, other variables that affect the response can be distributed unevenly among the treatment groups, thus biasing the experiment in one direction. A third type of design, known as matched pairs addresses this problem. In a matched pairs experiment, pairs of people are matched on as many variables as possible, so that the comparison happens between very similar cases. This is actually a special type of blocked experiment, where the blocks are of size two.
An alternate form of matched pairs involves each subject receiving both treatments. Randomization can be incorporated by randomly selecting half the subjects to receive treatment 1 first, followed by treatment 2, while the other half receives treatment 2 first, followed by treatment.
Checkpoint 1.5.4.
How and why should randomization be incorporated into a matched pairs design? 5
Checkpoint 1.5.5.
Matched pairs sometimes involves each subject receiving both treatments at the same time. For example, if a hand lotion was being tested, half of the subjects could be randomly assigned to put Lotion A on the left hand and Lotion B on the right hand, while the other half of the subjects would put Lotion B on the left hand and Lotion A on the right hand. Why would this be a better design than a completely randomized experiment in which half of the subjects put Lotion A on both hands and the other half put Lotion B on both hands? 6
Because it is essential to identify the type of data collection method used when choosing an appropriate inference procedure, we will revisit sampling techniques and experiment design in the subsequent chapters on inference.
Subsection 1.5.5 Testing more than one variable at a time
Some experiments study more than one factor (explanatory variable) at a time, and each of these factors may have two or more levels (possible values). For example, suppose a researcher plans to investigate how the type and volume of music affect a person's performance on a particular video game. Because these two factors, type and volume, could interact in interesting ways, we do not want to test one factor at a time. Instead, we want to do an experiment in which we test all the combinations of the factors. Let's say that volume has two levels (soft and loud) and that type has three levels (dance, classical, and punk). Then, we would want to carry out the experiment at each of the six (\(2 \times 3 = 6\)) combinations: soft dance, soft classical, soft punk, loud dance, loud classical, loud punk. Each of the these combinations is a treatment. Therefore, this experiment will have 2 factors and 6 treatments. In order to replicate each treatment 10 times, one would need to play the game 60 times.
Checkpoint 1.5.6.
A researcher wants to compare the effectiveness of four different drugs. She also wants to test each of the drugs at two doses: low and high. Describe the factors, levels, and treatments of this experiment. 7
As the number of factors and levels increases, the number of treatments become large and the analysis of the resulting data becomes more complex, requiring the use of advanced statistical methods. We will investigate only one factor at a time in this book.
Subsection 1.5.6 Section summary
In an experiment, researchers impose a treatment to test its effects. In order for observed differences in the response to be attributed to the treatment and not to some other factor, it is important to make the treatment groups and the conditions for the treatment groups as similar as possible.
Researchers use direct control, ensuring that variables that are within their power to modify (such as drug dosage or testing conditions) are made the same for each treatment group.
Researchers randomly assign subjects to the treatment groups so that the effects of uncontrolled and potentially confounding variables are evened out among the treatment groups.
Replication, or imposing the treatments on many subjects, gives more data and decreases the likelihood that the treatment groups differ on some characteristic due to chance alone (i.e. in spite of the randomization).
An ideal experiment is randomized, controlled, and double-blind.
A completely randomized experiment involves randomly assigning the subjects to the different treatment groups. To do this, first number the subjects from 1 to N. Then, randomly choose some of those numbers and assign the corresponding subjects to a treatment group. Do this in such a way that the treatment group sizes are balanced, unless there exists a good reason to make one treatment group larger than another.
In a blocked experiment, subjects are first separated by a variable thought to affect the response variable. Then, within each block, subjects are randomly assigned to the treatment groups as described above, allowing the researcher to compare like to like within each block.
When feasible, a matched-pairs experiment is ideal, because it allows for the best comparison of like to like. A matched-pairs experiment can be carried out on pairs of subjects that are meaningfully paired, such as twins, or it can involve all subjects receiving both treatments, allowing subjects to be compared to themselves.
A treatment is also called a factor or explanatory variable. Each treatment/factor can have multiple levels, such as yes/no or low/medium/high. When an experiment includes many factors, multiplying the number of levels of the factors together gives the total number of treatment groups.
In an experiment, blocking, randomization, and direct control are used to control for confounding factors.
Exercises 1.5.7 Exercises
1. Light and exam performance.
A study is designed to test the effect of light level on exam performance of students. The researcher believes that light levels might have different effects on males and females, so wants to make sure both are equally represented in each treatment. The treatments are fluorescent overhead lighting, yellow overhead lighting, no overhead lighting (only desk lamps).
What is the response variable?
What is the explanatory variable? What are its levels?
What is the blocking variable? What are its levels?
(a) Exam performance.
(b) Light level: fluorescent overhead lighting, yellow overhead lighting, no overhead lighting (only desk lamps).
(c) Sex: man, woman.
2. Vitamin supplements.
To assess the effectiveness of taking large doses of vitamin C in reducing the duration of the common cold, researchers recruited 400 healthy volunteers from staff and students at a university. A quarter of the patients were assigned a placebo, and the rest were evenly divided between 1g Vitamin C, 3g Vitamin C, or 3g Vitamin C plus additives to be taken at onset of a cold for the following two days. All tablets had identical appearance and packaging. The nurses who handed the prescribed pills to the patients knew which patient received which treatment, but the researchers assessing the patients when they were sick did not. No significant differences were observed in any measure of cold duration or severity between the four medication groups, and the placebo group had the shortest duration of symptoms. 8
Was this an experiment or an observational study? Why?
What are the explanatory and response variables in this study?
Were the patients blinded to their treatment?
Was this study double-blind?
Participants are ultimately able to choose whether or not to use the pills prescribed to them. We might expect that not all of them will adhere and take their pills. Does this introduce a confounding variable to the study? Explain your reasoning.
3. Light, noise, and exam performance.
A study is designed to test the effect of light level and noise level on exam performance of students. The researcher believes that light and noise levels might have different effects on males and females, so wants to make sure both are equally represented in each treatment. The light treatments considered are fluorescent overhead lighting, yellow overhead lighting, no overhead lighting (only desk lamps). The noise treatments considered are no noise, construction noise, and human chatter noise.
What type of study is this?
How many factors are considered in this study? Identify them, and describe their levels.
What is the role of the sex variable in this study?
(a) Exam performance.
(b) Light level (overhead lighting, yellow overhead lighting, no overhead lighting) and noise level (no noise, construction noise, and human chatter noise).
(c) Since the researchers want to ensure equal gender representation, sex will be a blocking variable.
4. Music and learning.
You would like to conduct an experiment in class to see if students learn better if they study without any music, with music that has no lyrics (instrumental), or with music that has lyrics. Briefly outline a design for this study.
5. Soda preference.
You would like to conduct an experiment in class to see if your classmates prefer the taste of regular Coke or Diet Coke. Briefly outline a design for this study.
Need randomization and blinding. One possible outline: (1) Prepare two cups for each participant, one containing regular Coke and the other containing Diet Coke. Make sure the cups are identical and contain equal amounts of soda. Label the cups A (regular) and B (diet). (Be sure to randomize A and B for each trial!) (2) Give each participant the two cups, one cup at a time, in random order, and ask the participant to record a value that indicates how much she liked the beverage. Be sure that neither the participant nor the person handing out the cups knows the identity of the beverage to make this a double- blind experiment. (Answers may vary.)
6. Exercise and mental health.
A researcher is interested in the effects of exercise on mental health and he proposes the following study: Use stratified random sampling to ensure representative proportions of 18-30, 31-40 and 41- 55 year olds from the population. Next, randomly assign half the subjects from each age group to exercise twice a week, and instruct the rest not to exercise. Conduct a mental health exam at the beginning and at the end of the study, and compare the results.
What type of study is this?
What are the treatment and control groups in this study?
Does this study make use of blocking? If so, what is the blocking variable?
Does this study make use of blinding?
Comment on whether or not the results of the study can be used to establish a causal relationship between exercise and mental health, and indicate whether or not the conclusions can be generalized to the population at large.
Suppose you are given the task of determining if this proposed study should get funding. Would you have any reservations about the study proposal?
Chapter Highlights.
Chapter 1 focused on various ways that researchers collect data. The key concepts are the difference between a sample and an experiment and the role that randomization plays in each.
Researchers take a random sample in order to draw an inference to the larger population from which they sampled. When examining observational data, even if the individuals were randomly sampled, a correlation does not imply a causal link.
In an experiment, researchers impose a treatment and use random assignment in order to draw causal conclusions about the effects of the treatment. While often implied, inferences to a larger population may not be valid if the subjects were not also randomly sampled from that population.
Related to this are some important distinctions regarding terminology. The terms stratifying and blocking cannot be used interchangeably. Likewise, taking a simple random sample is different than randomly assigning individuals to treatment groups.
Stratifying vs Blocking. Stratifying is used when sampling, where the purpose is to sample a subgroup from each stratum in order to arrive at a better estimate for the parameter of interest. Blocking is used in an experiment to separate subjects into blocks and then compare responses within those blocks. All subjects in a block are used in the experiment, not just a sample of them.
Random sampling vs Random assignment. Random sampling refers to sampling a subset of a population for the purpose of inference to that population. Random assignment is used in an experiment to separate subjects into groups for the purpose of comparison between those groups.
When randomization is not employed, as in an observational study, neither inferences nor causal conclusions can be drawn. Always be mindful of possible confounding factors when interpreting the results of observation studies.
