Advanced High School Statistics: Second Edition, with updates based on AP© Statistics Course Framework

Subsection 4.4.1 Learning objectives

• Determine if a scenario is binomial.

• Calculate the probabilities of the possible values of a binomial random variable.

• Calculate and interpret the mean (expected value) and standard deviation of the number of successes in \(n\) binomial trials.

• Determine whether a binomial distribution can be modeled as approximately normal. If so, use normal approximation to estimate cumulative binomial probabilities.

Subsection 4.4.2 An example of a binomial distribution

In Example 3.3.6, we asked various probability questions regarding the number of people out of 4 with blood type O+. We verified that the scenario was binomial and that each problem could be solved using the binomial formula. Instead of looking at it piecewise, we could describe the entire distribution of possible values and their corresponding probabilities. Since there are 4 people, there are several possible outcomes for the number who might have blood type O+: 0, 1, 2, 3, 4. We can make a distribution table with these outcomes. Recall that the probability of a randomly sampled person being blood type O+ is about 0.35.

\(x_i\)	\(P(x_i)\)
0	\({4\choose 0}(0.35)^0(0.65)^{4} = 0.179\)
1	\({4\choose 1}(0.35)^1(0.65)^{3} = 0.384\)
2	\({4\choose 2}(0.35)^2(0.65)^{2} = 0.311\)
3	\({4\choose 3}(0.35)^3(0.65)^{1} = 0.111\)
4	\({4\choose 4}(0.35)^4(0.65)^{0} = 0.015\)

Subsection 4.4.3 The mean and standard deviation of a binomial distribution

Since this is a probability distribution we could find its mean and standard deviation using the formulas from Chapter 3. Those formulas require a lot of calculations, so it is fortunate there's an easier way to compute the mean and standard deviation for a binomial random variable.

The exact distribution is shown in Figure 4.4.3.

Subsection 4.4.4 Normal approximation to the binomial distribution

The binomial formula is cumbersome when the sample size (\(n\)) is large, particularly when we consider a range of observations.

The computations in Example 4.4.4 are tedious and long. In general, we should avoid such work if an alternative method exists that is faster, easier, and still accurate. Recall that calculating probabilities of a range of values is much easier in the normal model. In some cases we may use the normal distribution to estimate binomial probabilities. While a normal approximation for the distribution in Figure 4.4.1 when the sample size was \(n = 4\) would not be appropriate, it might not be too bad for the distribution in Figure 4.4.3 where \(n = 40\text{.}\) We might wonder, when is it reasonable to use the normal model to approximate a binomial distribution?

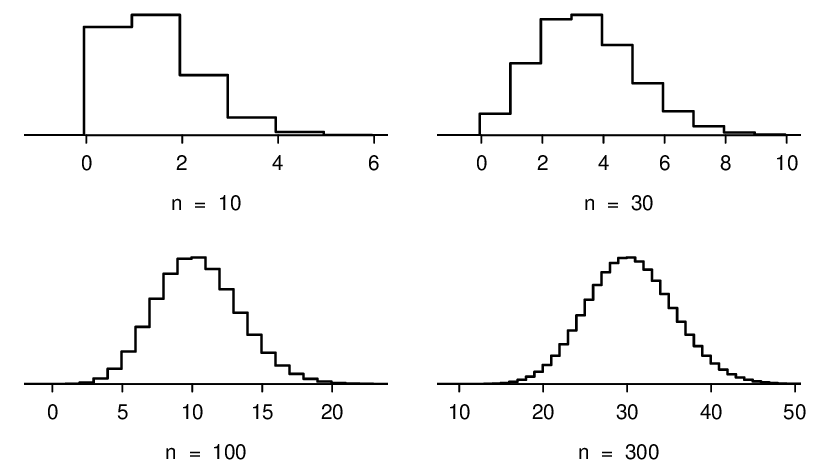
The shape of the binomial distribution depends upon both \(n\) and \(p\text{.}\) Here we introduce a rule of thumb for when normal approximation of a binomial distribution is reasonable. We will use this rule of thumb in many applications going forward.

The normal approximation may be used when computing the range of many possible successes. For instance, we may apply the normal distribution to the setting described in Figure 4.4.3.

Use the normal approximation to estimate the probability of observing fewer than 12 with blood type O+ in a random sample of 40, if the true proportion with blood type O+ in the population is \(p=0.35\text{.}\)

Solution

First we verify that \(np\) and \(n(1-p)\) are at least 10 so that we can apply the normal approximation to the binomial model:

\begin{align*} np\amp = 40(0.35)=14\ge 10 \amp n(1-p)\amp = 40(0.65) = 26\ge 10 \end{align*}

With these conditions checked, we may use the normal distribution to approximate the binomial distribution with the following mean and standard deviation:

\begin{align*} \mu \amp = np = 40(0.35)=14\\ \sigma \amp = \sqrt{np(1-p)} = \sqrt{40(0.35)(0.65)} = 3.0 \end{align*}

We want to find the probability of observing fewer than 12 with blood type O+ using this model. We note that 12 is less than 1 standard deviation below the mean:

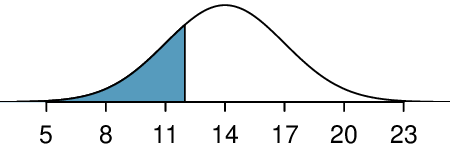
Next, we compute the Z-score as \(Z=\frac{12 - 14}{3} = -0.67\) to find the shaded area in the picture: \(P(Z \lt -0.67) = 0.25\text{.}\) This probability of 0.25 using the normal approximation is reasonably close to the true probability of 0.21 computed using the binomial distribution.

Use the normal approximation to estimate the probability of observing fewer than 120 people with blood type O+ in a random sample of 400, if the true proportion with blood type O+ in the population is \(p=0.35\text{.}\)

Solution

We have previously verified that the binomial model is reasonable for this context. Now we will verify that both \(np\) and \(n(1-p)\) are at least 10 so we can apply the normal approximation to the binomial model:

\begin{align*} np\amp =400(0.35)=140\ge 10 \amp n(1-p)\amp =400(0.65)=260\ge 10 \end{align*}

With these conditions checked, we may use the normal approximation in place of the binomial distribution with the following mean and standard deviation:

\begin{align*} \mu \amp = np = 400(0.35)=140\\ \sigma \amp = \sqrt{np(1-p)} = \sqrt{400(0.35)(0.65)}= 9.5 \end{align*}

We want to find the probability of observing fewer than 120 with blood type O+ using this model. We note that 120 is just over 2 standard deviations below the mean:

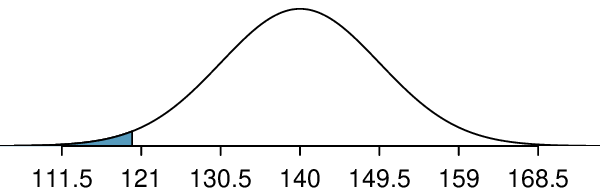
Next, we compute the Z-score as \(Z=\frac{120 - 140}{9.5} = -2.1\) to find the shaded area in the picture: \(P(Z \lt -2.1) = 0.0179\text{.}\) This probability of 0.0179 using the normal approximation is very close to the true probability of 0.0196 from the binomial distribution.

Subsection 4.4.5 Normal approximation breaks down on small intervals (special topic)

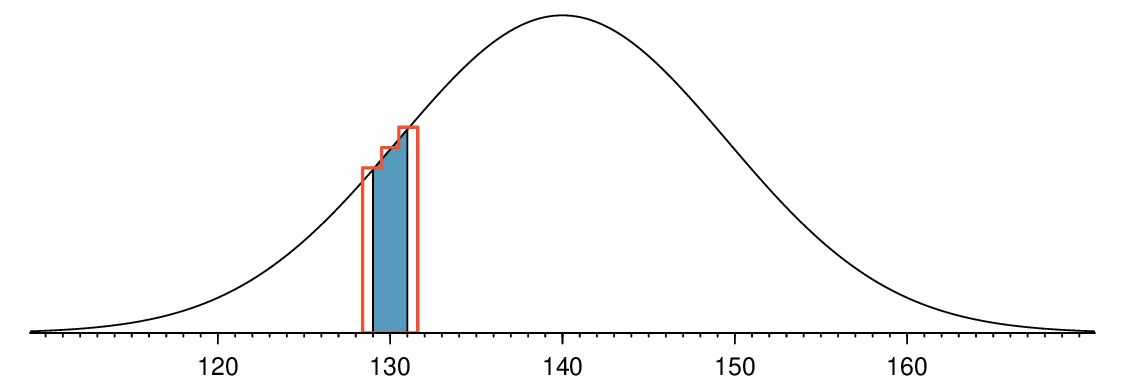
We consider again our example where 35% of people are blood type O+. Suppose we want to find the probability that between 129 and 131 people, inclusive, have blood type O+ in a random sample of 400 people. We want to compute the probability of observing 129, 130, or 131 people with blood type O+ when \(p=0.20\) and \(n=400\text{.}\) With such a large sample, we might be tempted to apply the normal approximation and use the range 129 to 131. However, we would find that the binomial solution and the normal approximation notably differ:

We can identify the cause of this discrepancy using Figure 4.4.10, which shows the areas representing the binomial probability (outlined) and normal approximation (shaded). Notice that the width of the area under the normal distribution is 0.5 units too slim on both sides of the interval. The binomial distribution is a discrete distribution, and the each bar is centered over an integer value. Looking closely at Figure 4.4.10, we can see that the bar corresponding to 129 begins at 128.5 and ends at 129.5, the bar corresponding to 131 begins at 130.5 and ends at 131.5, etc.

It is always possible to apply the continuity correction when finding a normal approximation to the binomial distribution. However, when \(n\) is very large or when the interval is wide, the benefit of the modification is limited since the added area becomes negligible compared to the overall area being calculated.

Subsection 4.4.6 Section summary

In the previous chapter, we introduced the binomial formula to find the probability of exactly \(x\) successes in \(n\) trials for an event that has probability \(p\) of success. Instead of looking at this scenario piecewise, we can describe the entire distribution of the number of successes and their corresponding probabilities.

• The distribution of the number of successes in \(n\) independent trials gives rise to a binomial distribution. If X has a binomial distribution with parameters \(n\) and \(p\text{,}\) then \(P(X=x) = {n\choose x}p^x(1-p)^n-x\text{,}\) where \(x=0,1,2,3\dots,n\text{.}\)

• To write out a binomial probability distribution table, list all possible values for \(x\text{,}\) the number of successes, then use the binomial formula to find the probability of each of those values.

• Because a binomial distribution can be thought of as the sum of a bunch of 0s and 1s, the Central Limit Theorem applies. As \(n\) gets larger, the shape of the binomial distribution becomes more normal.

• We call the rule of thumb for when the binomial distribution can be well modeled with a normal distribution the success-failure condition. The success-failure condition is met when there are at least 10 successes and 10 failures, or when \(np\ge 10\) and \(n(1-p)\ge 10\text{.}\)

• If X follows a binomial distribution with parameters \(n\) and \(p\text{,}\) then:

  • The mean is given by \(\mu_{\scriptscriptstyle{X}} = np\text{.}\) (center)

  • The standard deviation is given by \(\sigma_{\scriptscriptstyle{X}} = \sqrt{np(1-p)}\text{.}\) (spread)

  • When \(np\ge 10\) and \(n(1-p)\ge 10\text{,}\) the binomial distribution is approximately normal. (shape)

• It is often easier to use normal approximation to the binomial distribution rather than evaluate the binomial formula many times. These three properties of the binomial distribution are used when solving the following type of problem. Find the probability of getting more than / fewer than x yeses in \(n\) trials or in a sample of size \(n\).

  1. Identify \(n\) and \(p\text{.}\) Verify than \(np\ge 10\) and \(n(1-p)\ge 10\text{,}\) which implies that normal approximation is reasonable.

  2. Calculate the Z-score. Use \(\mu_{\scriptscriptstyle{X}} = np\) and \(\sigma_{\scriptscriptstyle{X}} = \sqrt{np(1-p)}\) to standardize the \(x\) value.

  3. Find the appropriate area under the normal curve.