Skip to main content

Worksheet 31.5 Dot products and projection
A4US

1.

Let \({\vec v}_1 = (-4,1)\text{,}\) \({\vec v}_2 = (2,2)\text{,}\) \({\vec v}_3 = (1,2,3)\text{,}\) \({\vec v}_4 = (-2,1,0)\text{.}\) Find the values of the following expressions:

(a)
\({\vec v}_1 \cdot {\vec v}_2 = \underline{\hspace{4.545454545454546em}}\)
(b)
\({\vec v}_3 \cdot {\vec v}_4 = \underline{\hspace{4.545454545454546em}}\)
(c)
\(\lVert{\vec v}_1\rVert = \underline{\hspace{4.545454545454546em}}\)
(d)
\(\lVert{\vec v}_4\rVert = \underline{\hspace{4.545454545454546em}}\)
(e)

Are any of these vectors perpendicular to each other?

Go to previous slideGo to next slide

2.

The vectors \(\vec a = (3,9)\) and \(\vec u = (4,2)\) are pictured below. Derive the formula for projection on a line and use it to find the projection of \(\vec a\) on the line spanned by \(\vec u\text{.}\) Also compute the length of the residual vector.

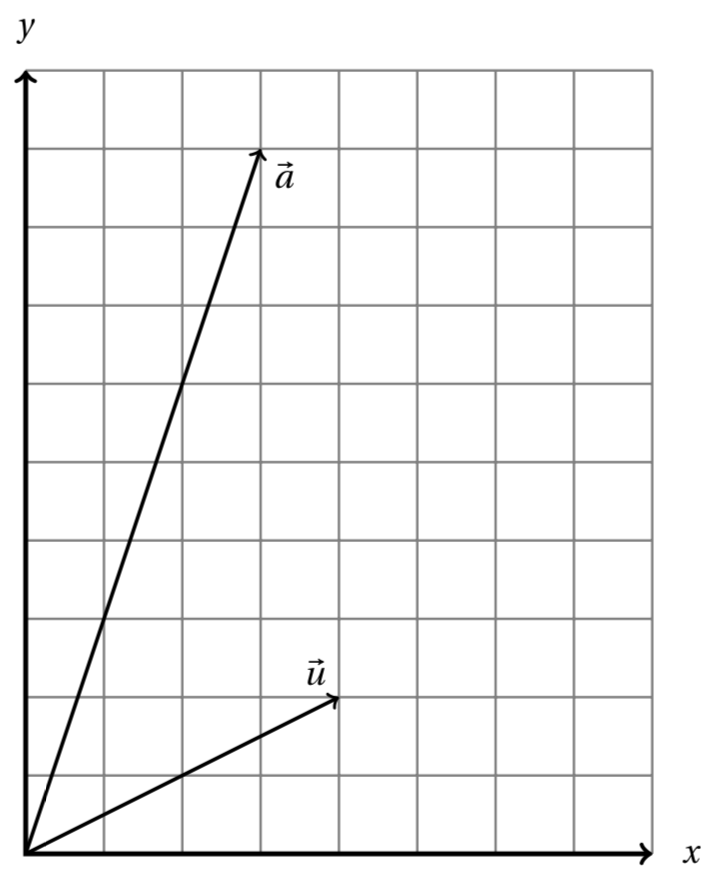
two vectors...
Go to previous slideGo to next slide

3.

Consider the vector equation

\begin{equation*} m \begin{bmatrix}2 \\ 5\end{bmatrix} = \begin{bmatrix}3 \\ 7\end{bmatrix}\text{.} \end{equation*}
(a)

Check that there is no solution \(m\) that makes the equation true.

(b)

Use projection to find the best approximation \(\hat m\text{.}\)

(c)

Compute \(\hat m \begin{bmatrix}2 \\ 5\end{bmatrix} \text{.}\)

(d)

Compute the residual vector.

(e)

Compute the length of the residual vector and explain what it means.

Go to previous slideGo to next slide

4.

Consider the system of equations

\begin{align*} 3t \amp =5\\ 2t \amp = 9 \text{.} \end{align*}
(a)

Write the system in vector form.

(b)

Find the best estimate, \(\hat t\text{,}\) of \(t\) using projection.

(c)

Compute the length of the residual vector.

Go to previous slideGo to next slide