Skip to main content
🔗

Section 2.1 Introduction to Spreadsheets

🔗
A spreadsheet such as Google Sheets or Microsoft Excel, is a very useful tool for doing calculations and making complex tables. You can type in your own custom calculations or use the built-in formulas.

🔗
The rectangles within a spreadsheet are called cells, and they can be referenced by their column letter and row number. The first cell in the upper left side highlighted below is A1. If we wanted to talk about the third column and the fifth row, that cell would be C5.

A blank spreadsheet with the cell A1 highlighted

🔗
A spreadsheet file can contain many sheets. Look along the bottom to see if there is more than one sheet and make sure you are on the right sheet.

A blank spreadsheet showing the sheet tabs at the bottom of the screen.
🔗

Subsection 2.1.1 Basic Calculations

🔗
To do a calculation on a spreadsheet, type an equal sign before the operation. This lets the program know that you want it to calculate the result. When you press enter, you will see the result.

🔗
Example 2.1.1.

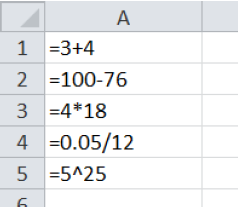
  1. To add 3 + 4, enter =3+4

  2. To subtract 100-76, enter =100-76

  3. To multiply 4 times 18, enter =4*18

  4. To divide 0.05 by 12, enter =0.05/12

  5. To calculate 525,525, enter =5^25

A spreadsheet showing the examples entered in the spreadsheet. cell A1 has =3+4, cell A2 has =100-76, cell A3 has =4*18, cell A4 has =0.05/12 and cell A5 has =5^25.

🔗
Note that the asterisk (*) is used for multiplication. Spreadsheets don’t recognize parentheses as indicators of multiplication like calculators do, so even if you have parentheses for the order of operations, the asterisk is also needed.

🔗
You can make more complicated mathematical expressions using parentheses and other operations. To edit a cell click on the editing box at the top, or double click on the cell to edit it directly.

🔗
Example 2.1.2.

Your bill at a restaurant is $35.75 and you want to leave an 18% tip. How much would you add to the bill?

Solution

To work with a percentage, we need to convert it into a decimal first, and then multiply it by the base amount.

In a spreadsheet we would type

=0.18*35.75

and get a result of $6.44, rounded to the nearest cent. You would leave a tip of $6.44.

🔗

Subsection 2.1.2 Cell References

🔗
One of the powerful things about spreadsheets is using a cell reference, such as C5 in a calculation. When you use a cell reference, the values will automatically update if any of the referenced values change.

🔗
Let’s make a spreadsheet for the percentage tip example above. We calculated an 18% tip on a bill of $35.75. We might want to tip 18% in general, but our bill will change values. We labeled the first column Bill Amount and the second column Tip. The amount of $35.75 is entered in cell A2. Then when we write our formula in B2, we want to calculate 18% of A2. That way if the number in A2 changes, our tip will automatically update.

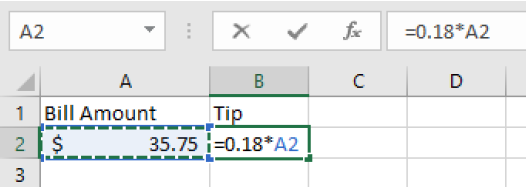
A spreadsheet showing a formula with a cell reference, =0.18*A2

🔗
The formula

=0.18*A2

🔗
is entered in B2 which gives a result of $6.44 when you hit enter.

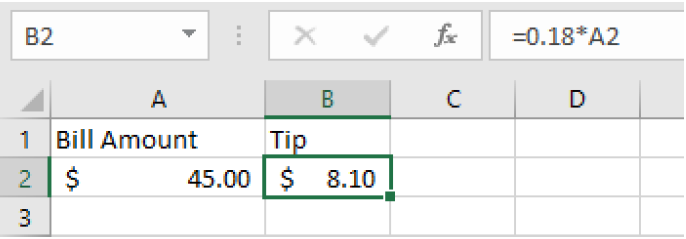
The same spreadsheet showing when the input in A1 is changed to $45, the answer to the formula changes to $8.10.

🔗
When the bill amount is changed, the tip is recalculated.

🔗

Subsection 2.1.3 Cell Formatting

🔗
We can also format cells A1 and B1 to show dollar signs by clicking on the dollar sign in the number formatting menu.

🔗

Subsection 2.1.4 Fill-Down Feature

🔗
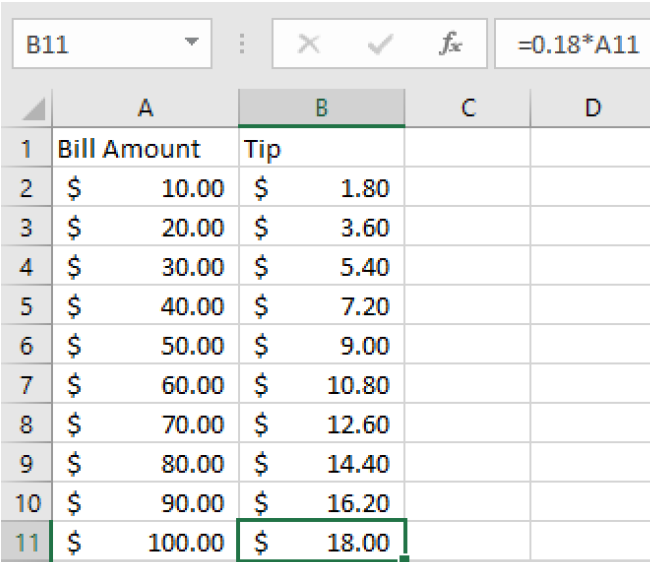
The fill-down feature is very useful for making tables. This allows us to copy values or formulas to save time. Let’s make a tipping reference table with values from $10, to$100, in increments of $10. First, we will enter two values in column A to establish the pattern. Then select those two cells and you will see a small square in the lower right corner. Drag that square down until you get to $100.

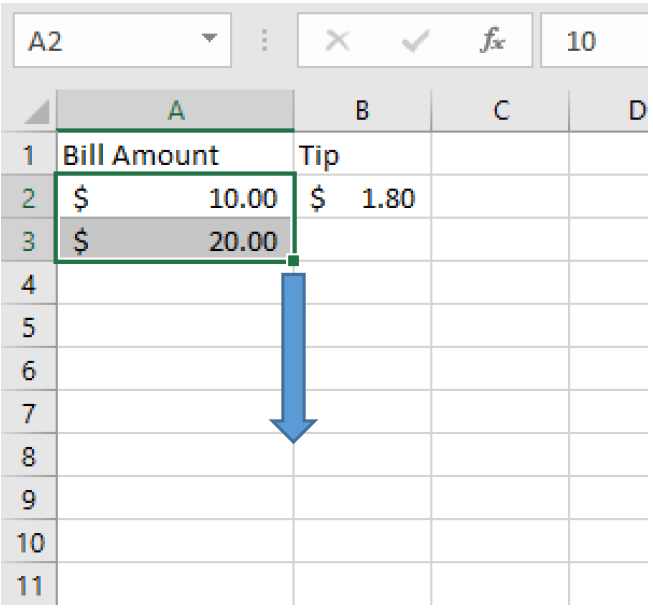
A spreadsheet showing the fill-down feature; cells A2 and A3 are highligted for the pattern and there is a down arrow by the small square to drag down.
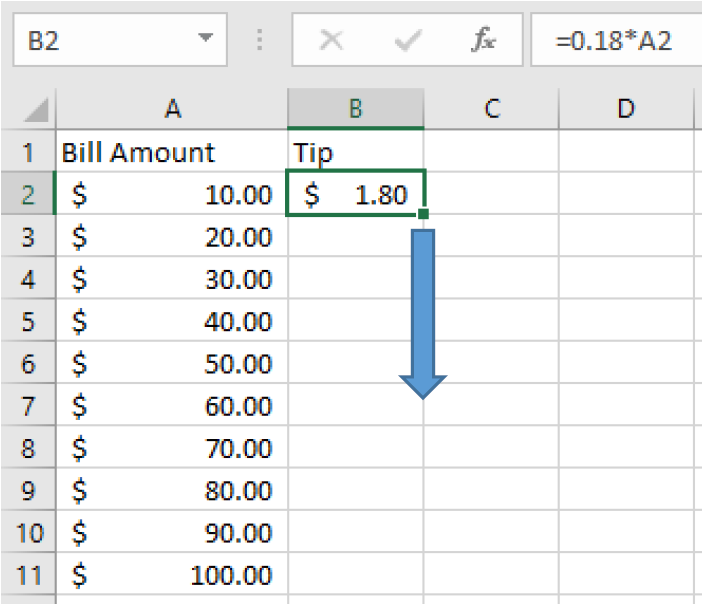
This spreadsheet shows the completed bill amount column from $10 to $100 and shows the fill-down feature for the formula; cell B2 has the equation =0.18*A2 and there is a down arrow by the small square to drag down.

🔗
Next, we can drag our formula down and the cell reference will change to each row number automatically.

🔗
Here are the formulas with the row numbers updated:

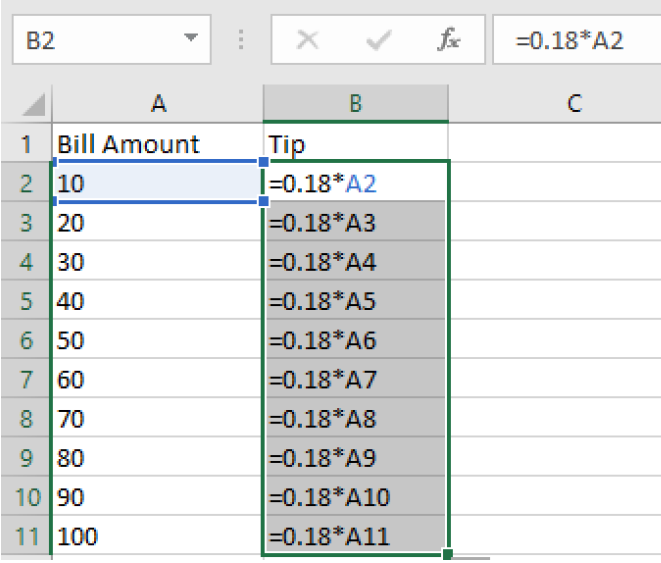
This spreadsheet shows the result of filling down the formula. The cell reference changes for each new row.

🔗
Here is our completed table with the calculations:

This spreadsheet shows the calculated values for tips from $10-100.
🔗

Subsection 2.1.5 Formulas

🔗
Spreadsheets have many useful built-in formulas. We will introduce some of the financial formulas in this chapter. Here are some of the formulas we will use:

  1. =FV to calculate the future values of an investment

  2. =PV to calculate the deposit needed for a desired future balance

  3. =PMT to calculate a loan or savings plan payment

  4. =EFFECT to calculate the effective rate of an account and compare accounts

🔗
In the rest of this chapter we will use spreadsheets and formulas to calculate the future values, interest paid or earned and monthly payments.

🔗

Exercises 2.1.6 Exercises

🔗
Use a spreadsheet to compute the following.

🔗
1.

Convert 4/74/7 to a decimal

Solution

=4/7 which gives approximately 0.571429

🔗
2.

Convert 16% to a decimal

Solution

=16% which gives 0.16

🔗
4.

Find the difference of 230 and 78

Solution

=230-78 which gives 152

🔗
6.

Divide 0.09 by 52

Solution

=0.09/52 which gives approximately 0.001731

🔗
8.

Your bill at a restaurant is $55.75 and you want to leave a 20% tip. How much would you add to the bill?

Solution

=55.75*20% which gives 11.15 or eleven dollars and fifteen cents

🔗
9.

You leave a tip for $7.50 for a bill at a restaurant that is $44.50. What percent tip did you leave?

Solution

=7.50/44.50 which gives approximately 0.168539, or approximately 16.8539%

🔗
10.

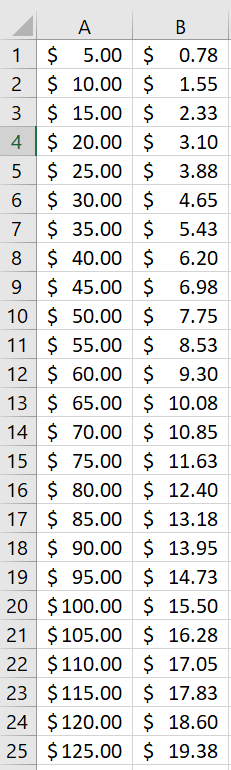
In Column A use the fill down feature to build a spreadsheet starting with $5 and ending at $125, in increments of $5. In Column B write a formula with a cell reference to calculate a 15.5% tip on the amount in Column A. Use the fill down feature to complete your table.

Solution

See the table below:

Note, the entry in cell B1 is =15%*A1. (Columns A and B are given dollar formatting)

A portion of a spreadsheet is shown which includes cells A1 through B25, and with a title heading of Table 1. Cell A1 shows $5.00, cell A2 shows $10.00, and so on. The pattern shows that each additional cell under A1 is equal to the cell above it, plus $5.00. This pattern continues down to cell A25, which shows $125.00. Cell B1 shows $0.78, which is 15% of the $5.00 amount shown in cell A1. Cell B2 shows $1.55, which is 15% of the $10.00 amount shown in cell A2. This pattern continues until we reach cell B25, which shows $19.38, and which is 15% of the $125.00 amount shown in cell A25.
🔗
11.

Imagine a certain savings account started out with a balance of $5250.00 on day-one, and today has a current balance of $5780.23

  1. Exactly how much more money does the account have today, compared with day-one?

  2. Rounding to the nearest tenth of a percent: By what percentage amount has the account balance grown?

  3. If instead, the bank balance today was exactly double the starting balance, then by what exact percentage amount would the bank balance have grown?

  4. If the bank balance today had instead grown by 15.5% since day-one, then what would be the exact amount of today’s balance?

Solution

  1. =5780.23-5250 which gives 530.23 dollars

  2. =530.23/5250 which gives approximately 0.100996, or approximately 10.1%

  3. Exactly 200%

  4. =5250*115.5% which gives exactly 6063.75 dollars

🔗
12.

Imagine that at the start of a certain month, you will make an opening deposit of $500 into a savings account, and you will then leave the account alone (meaning you will make no further deposits or withdrawals). Also, for this account: Every month after the opening deposit, the amount in the account will grow to be 101% of its previous month’s balance.

  1. Use a spreadsheet to enter 500 in cell A1. Using a formula and a cell-reference: Compute in cell A2, the amount in the account after one month has passed. Then using the fill down feature, continue the pattern for another eleven full months (you should end at cell A13). Format all the cells to show dollar signs. What is the amount in the account after one year?

  2. Now continue the pattern in column A of your spreadsheet to extend for a second full year (you should end at cell A25). What is the amount in the account after two years?

  3. What overall percentage growth occurred in the account between the opening deposit and one year later? (Compute using a formula and cell references)

  4. What overall percentage growth occurred in the account between the end of year one, and the end of year two? (Compute using a formula and cell references)

  5. (Challenge) The annual percentage growth that you found in part (d) for the second year, should be identical to the annual percentage growth that you found in part (c) for the first year. Can you mathematically explain why this is true? Do you think this pattern of identical overall annual percentage growth would continue, if you extend the pattern for even more years?

Solution

  1. See the table at the bottom for part a and part b.

    After 1 year, the account holds $563.41

  2. See the table at the bottom for part a and part b.

    After 2 years, the account holds $634.87

  3. =A13/A1 which gives \(\approx 112.6825\%\) growth

  4. =A25/A13 which gives \(\approx 112.6825\%\) growth (same)

  5. Each starting value increases mathematically by a factor of \((1.01)^{12}\) each year, which is \(\approx 112.6825\%\text{.}\) So yes, this pattern must continue indefinitely into future years.

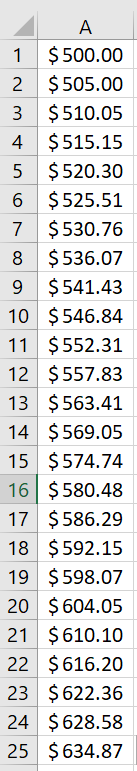
A portion of a spreadsheet is shown covering cells A1 through A25, and with a title heading of Table 2. Cell A1 shows $500.00. Cell A2 shows $505.00, which is 101% of cell A1. Cell A3 shows $510.05, which is 101% of cell A2. This pattern continues until we reach cell A25, which shows $634.87, and which is 101% of cell A24.
🔗
13.

Imagine that at the start of a certain year, you will deposit $1000.00 into a savings account, and then you will leave the account alone. Each year after the opening deposit, the amount in the account will grow to be 103% of its previous year’s balance.

  1. After two years, the account balance will have experienced two growth amounts of 103%. You can find this account balance amount here, with the spreadsheet computation = 1000 * (103%) * (103%). Perform this computation in a spreadsheet and write the balance that you find.

  2. Now enter the spreadsheet computation = 1000 * (103%)^2. Notice that the result here, which involves using a power, gives the same answer as you found in part (a). Comparing the two spreadsheet computations: Explain why they give the same result.

  3. Using the pattern in part (b) above, and carefully choosing the power: Compute the balance that will be in the account fifteen full years after the account was originally opened. (Round to the nearest cent)

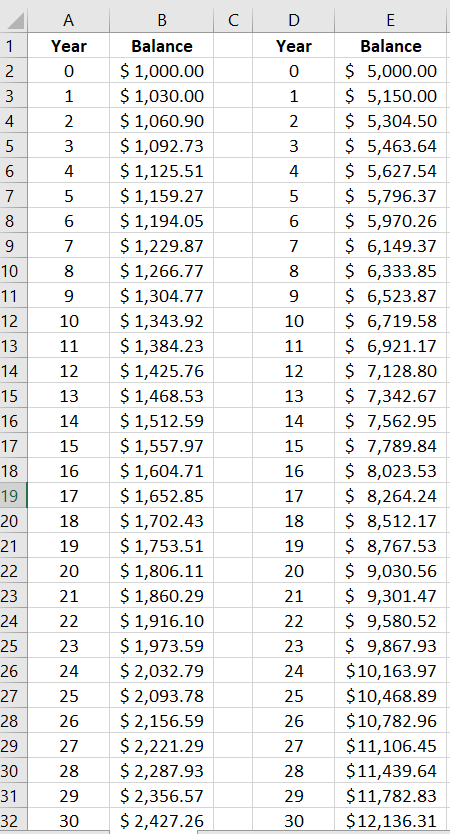
  4. (Challenge) Make a spreadsheet that shows the account balance each individual year for 30 years. From the date of the opening deposit: What minimum number of full years will you have to wait, until the balance finally exceeds twice its opening deposit amount? (Use cell references, the fill down feature, and dollar formatting)

  5. (Challenge) Imagine the opening balance of the account was $5000.00 instead of $1000.00 (and everything else about the account stays the same). Make a similar spreadsheet as you did in part (d), and using this spreadsheet, find the minimum number of full years you will have to wait this time, until the balance finally exceeds twice its opening deposit amount. How does this answer compare with your answer in part (d)? Do you think your answer would be the same here, for any positive opening balance you may choose for the account?

Solution

  1. =1000*103%*103% which gives 1060.90 dollars.

  2. =1000*(103%)^2 gives the same result of 1060.90 dollars, because raising 103% to the second power means the same as multiplying 103% by itself two times.

  3. =1000*(103%)^15 which gives 1557.97 dollars (to the nearest cent).

  4. Refer to the table at the bottom for part d and part e.

    Note the entry in cell B3 here is = B2*103% and the remaining cells are computed using the fill down feature.

    You will have to wait a minimum of 24 full years, in each case, in order for the balance to finally exceed twice the opening deposit amount.

  5. Since \((103\%)^{23} \lt 2 \lt (103\%)^{24}\text{,}\) the minimum number of full years until the opening deposit doubles must be the same here, for any positive opening balance that we may choose for this account.

A portion of a spreadsheet is shown, which includes cells A1 through E32, and with a title heading of Table 3. Cell A1 shows a column title of Year, and cells A2 through A32 contain values of 0 through 30, respectively. Cells D1 through D32 are a copy of cells A1 through A32. Cell B1 shows a column title of Balance. Cell B2 shows $1,000.00, which corresponds to Year 0 displaying in adjacent cell A1. Cell B3 shows $1,030.00, which is 103% of the $1,000 shown in cell B2. Cell B4 shows $1,060.90, which is 103% of the $1,030.00 shown in cell B3. This pattern continues until we get to cell B32, which shows $2,427.26, and which is 103% of the $2,356.57 amount shown in cell B31. Cell E1 shows a column title of Balance. Cell B2 shows $5,000.00, which corresponds to Year 0 displaying in adjacent cell D1. Cell E3 shows $5,150.00, which is 103% of the $5,000 shown in cell E2. Cell E4 shows $5,304.50, which is 103% of the $5,150.00 shown in cell E3. This pattern continues until we get to cell E32, which shows $12,136.31, and which is 103% of the $11,782.83 amount shown in cell E31.